Основной закон теплопроводности

ЗАДАЧИ НЕСТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ В ТЕХНОЛОГИИ КПЭ

ОГЛАВЛЕНИЕ

1.			Физические основы передачи тепла
	1.1		Температурное поле
	1.2		Основной закон теплопроводности
	1.3		Модели источников теплоты
	1.4		Модели обрабатываемых деталей
	1.5		Температурное поле мгновенного точечного источника теплоты (МТИ)
		1.5.1	Температурное поле МТИ в полубесконечном теле
		1.5.2	Температурное поле мгновенного линейного источника
		1.5.3	Температурное поле мгновенного плоского источника
	1.6		Температурное поле точечного источника теплоты постоянной интенсивности (ПТИ)
		1.6.1	Температурное поле ПТИ в полубесконечном теле
		1.6.2	Температурное поле постоянно действующего линейного источника (ПЛИ)
		1.6.3	Температурное поле постоянно действующего плоского источника (ППИ)
	1.7		Температурное поле импульсного точечного источника теплоты (ИТИ) в полубесконечном теле.
			Работа с системой MATLAB
	2.1		Введение
	2.2		Рабочая среда MATLAB.
	2.3		Основные объекты MATLAB
	2.4		Просмотр и уничтожение переменных
	2.5		Форматы вывода результатов вычислений
	2.6		Операторы и функции
	2.7		Работа с массивами данных
	2.8		Векторы-столбцы, векторы-строки, сложение и вычитание векторов.
	2.9		Поэлементные операции с векторами
	2.10		Построение таблицы значений функции
	2.11		Основы графического представления результатов вычислений.
		2.11.1	Построение графика функций одной переменной
		2.11.2	Построение трехмерных графиков.
	2.12		Основы программирования.
	2.13		М-файлы.
	2.14		Особенности применения MATLAB для исследования температурных полей.

ФИЗИЧЕСКИЕ ОСНОВЫ ПЕРЕДАЧИ ТЕПЛА

Энергия необходимая для обработки деталей, переносится на поверхность материала с помощью различных субстанциональных потоков. Это концентрированные потоки заряженных частиц – электронов или ионов, их смеси – плазмы, световой поток, возможны и другие варианты. Часть соответствующего субстанционального потока проникает в материал детали на некоторую глубину, а другая часть отражается. Та часть потока, которая попала в материал, передаёт ему в результате торможения, некоторую долю своей энергии. Эта энергия идёт на разогрев материала детали и на его фазовые переходы – рекристаллизацию, плавление и испарение.

Для практических целей большое значение имеет теоретическая оценка положения границ фазовых переходов в зависимости от характера и интенсивности воздействия на обрабатываемый материал концентрированных потоков энергии (КПЭ), так как цели обработки достигаются именно путём осуществление этих фазовых переходов. Для получения таких оценок необходимо знание распределения температуры внутри обрабатываемого тела. Подробный и детальный анализ процессов распространения тепла даёт аналитическая теория теплопроводности.

Рассмотрим основные положения этой теории и механизмы передачи тепла теплопроводностью в твердых телах.

Передачу тепла от одной части тела к другой или от одного тела к другому, находящемуся в соприкосновении с первым, обычно называют теплопроводностью. Аналитическая теория теплопроводности игнорирует молекулярное строение вещества. Она рассматривает вещество не как совокупность отдельных дискретных частиц, а как сплошную среду—континуум. Такое модельное представление вещества может быть принято при решении задач на распространение тепла при условии, если размеры дифференциальных объемов достаточно велики по сравнению с размерами молекул и расстояниями между ними. Во всех расчетах и примерах тело предполагается однородным и изотропным.

Температурное поле

Всякое физическое явление, в том числе и процесс теплопередачи, происходит в пространстве и времени. Поэтому аналитическое исследование теплопроводности сводится к изучению пространственно временного изменения основной физической величины, характерной для данного явления — температуры, как функции пространственных координат и времени:

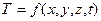(1)

Совокупность мгновенных значений температуры во всех точках изучаемого пространства называется температурным полем.

Так как температура есть величина скалярная, то и температурное поле является скалярным полем.

Различают стационарное температурное поле и нестационарное температурное поле.

Нестационарным температурным полем называется такое поле, температура которого изменяется не только в пространстве, но и во времени.

Уравнение (1) есть математическая запись нестационарного температурного поля.

Стационарным температурным полем называется такое поле, температура которого в любой его точке не изменяется во времени, т. е является функцией только координат.

В некоторых задачах стационарное температурное поле является асимптотическим случаем нестационарного.

Температурное поле, соответствующее уравнению (1) является пространственным – трехмерным.

Если температура есть функция двух координат, то поле называется двухмерным.

Если же температура есть функция одной координаты, то поле называется одномерным.

Поверхность, в каждой точке которой, температура одинакова, называется изотермической.

Пересечение изотермических поверхностей плоскостью, дает семейство изотерм, - линий одинаковой температуры.

Изотермические поверхности и изотермические линии не пересекаются между собой и при непрерывном поле не обрываются внутри него.

Наибольший перепад температуры на единицу длины происходит в направлении нормали к изотермической поверхности.

Возрастание температуры в направлении нормали к изотермической поверхности характеризуется градиентом температуры. Градиент температуры есть вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры:

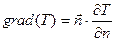(2)

Где 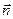— единичный вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры;

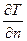- производная температуры по направлению нормали к изотермической поверхности.

Составляющие градиента по осям декартовых координат равны соответствующим частным производным:

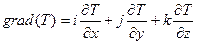
Это соотношение обусловлено тем обстоятельством, что любой вектор можно представить как векторную сумму трех векторов, направленных по координатным осям.

Можно ввести понятие напряженности температурного поля по определению:

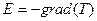
Вектор Е называется вектором напряженности температурного поля.

Основной закон теплопроводности.

Необходимым условием распространения тепла является наличие температурного градиента. Опыт показывает, что передача тепла теплопроводностью происходит по нормали к изотермической поверхности от мест с большей температурой к местам с меньшей температурой.

Количество тепла, проходящее в единицу времени и отнесенное к единице площади изотермической поверхности, называется плотностью теплового потока; соответствующий вектор определяется соотношением

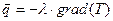
Вектор 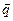называется вектором теплового потока, направление которого противоположно температурному градиенту (оба вектора направлены по нормали к изотермической поверхности, но в противоположные стороны).

Проекция вектора 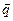на любое избранное направление есть тоже вектор.

Линии, касательные к которым совпадают с направлением вектора 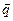, называются линиями теплового тока. Линии теплового тока перпендикулярны к изотермическим поверхностям в точках пересечения с ними. Касательная к линиям теплового тока, взятая в обратном направлении, дает нам направление градиента температуры.

Основной закон теплопроводности может быть сформулирован так: плотность теплового потока прямо пропорциональна напряженности температурного поля, или плотность теплового потока прямо пропорциональна градиенту температуры.

Количество теплоты необходимое для нагрева элементарного объёма материал 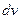до абсолютной температуры 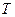, назовём теплосодержанием 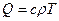(условно считаем, что давление 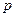постоянно, 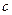- теплоёмкость, 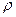- плотность). При изменении температуры меняется и теплосодержание материала. Изменение теплосодержания некоторого объёма материала 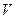, при изменении температуры внутри этого объёма:

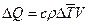(3),

где 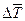- изменение средней по объёму температуры,

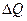- изменение теплосодержания.

Средняя по объёму температура может быть найдена путём интегрирования температурного поля по объёму и последующим делением на этот объём. Так если объём области ограничен сферой некоторого радиуса 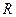, то элементарный объём равен 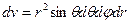, и среднюю температуру удобно искать в сферических координатах:

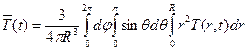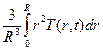= (4),

где 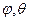- полярные углы,

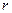- полярный радиус,

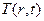- не стационарное температурное поле.

Среднее приращение температуры: 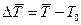, где 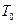- начальная температура.

Температурное поле может быть найдено путём решения уравнения теплопроводности, являющегося дифференциальной формой закона сохранения энергии:

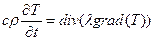. Если теплопроводность 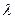, в первом приближении считать не зависящей, от температуры, то уравнение примет вид:

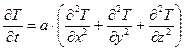(5)

где 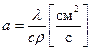- коэффициент температуропроводности.

1.3. Модели источников теплоты.

Та часть КПЭ, которая попала в материал, передаёт ему в результате торможения, некоторую долю своей энергии. Эта энергия идёт на разогрев материала детали и на его фазовые превращения, так, как если бы в объёме материала действовал распределённый объёмный источник тепла (ОИТ). Интенсивность ОИТ является функцией пространственных координат и времени, и имеет размерность- 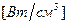. Доля поглощённой энергии характеризуется коэффициентом поглощения - 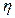. В общем случае коэффициент 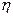зависит от температуры поверхности, однако для простаты будем считать его постоянным.

Поток энергии, попадающий на поверхность обрабатываемой детали, распределён по некоторому закону. В простейшем и самом распространённом случае это распределение является нормальным и круговым.

Величина, характеризующая падающий на поверхность поток, называется поверхностной плотностью мощности - ППМ, и измеряется в .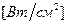

Для определения температурного поля внутри и на поверхности обрабатываемой детали, необходимо решить уравнение теплопроводности (5), с соответствующими начальными и граничными условиями с учётом параметров распределения ИТ. Вид и параметры распределения ИТ в материале зависят как от распределения ППМ, так и от вида и параметров субстанционального потока.

В общем случае решение оказывается достаточно сложным, поэтому прибегают к упрощениям, зависящим от решаемой задачи.

Для этого вводятся понятия идеализированных ИТ: плоского, линейного и точечного.

В случае плоского ИТ полагают, что тепло выделяется в бесконечно тонком слое, - плоский ИТ не имеет толщины. Интенсивность плоского ИТ измеряется в 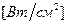. Если плоский ИТ расположен на поверхности тела, то он называется поверхностным плоским ИТ – ППИТ. Распределение интенсивности ППИТ совпадает с распределением поглощённой ППМ.

Линейный ИТ имеет только одно измерение. Величина, характеризующая его интенсивность, имеет размерность .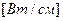

Точечный источник, - это источник вообще не имеющий линейных размеров. Интенсивность точечного источника измеряется в 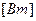. Идеальный точечный ИТ может быть помещён в любую точку нагреваемого тела. Если точечный ИТ расположен на поверхности тела, то он называется поверхностным точечным ИТ – ПТИТ.

Каждый из описанных идеальных источников классифицируется по времени действия:

- постоянно действующий,

- действующий, в течение заданного интервала времени,

- периодический,

- импульсный.

Каждый из перечисленных источников так же может быть подвижным или не подвижным. Температурные поля, создаваемые перечисленными идеальными источниками теплоты могут быть представлены, как сумма температурных полей, создаваемых мгновенными точечными источниками (МТИ).

Мгновенный точечный ИТ - понятие абстрактное. Размеры МТИ и время его действия стремятся к нулю. Такое введение теплоты можно рассматривать как начальное условие, когда при t=0 задается распределение теплоты в теле. Так, для мгновенного точечного ИТ можно принять, что только в точке с координатами 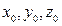при t=0 содержится количество теплоты Q, а во всех остальных точках тела теплосодержание будет постоянно и равно исходному. В следующие моменты времени теплота будет распространяться по телу, подчиняясь законам теплопроводности.

Непрерывно действующие и движущиеся ИТ представляют собой совокупность последовательно действующих мгновенных источников распределенных по времени действия источника.

Реальные источники моделируются идеальными ИТ приближённо.

Реальный точечный мгновенный ИТ - это источник, размеры которого, имея некоторую конечную величину, существенно меньше размеров нагреваемого тела. Расстояния, на которых исследуется температурное поле больше размеров источника, а распределение теплоты в самом источнике не влияет на характер температурного поля. За расчетную величину количества теплоты принимается полная теплота источника Q.

Реальный линейный ИТ - источник, размеры которого в двух направлениях (например, X и Y) существенно меньшие размеров нагреваемого тела, а в третьем (например, Z) - соизмерим или равны размеру тела в этом направлении ( 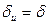). Теплота линейного источника распределена по этому направлению, а отвод тепла осуществляется в направлениях x и y.

Линейный ИТ представляет собой совокупность точечных источников, действующих одновременно по всей толщине и расположенных по линии .

При равномерном распределении теплоты по толщине детали (пластины) для расчета температурного поля за расчетную величину количества теплоты принимается теплота источника, отнесенная к толщине - .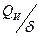

Используя принцип наложения, и комбинируя количество и порядок расположения мгновенных точечных ИТ, можно получить множество иных

ИТ.

Реальный плоский ИТ - источник, теплота которого распределена по площади поперечного сечения детали (направления x и y), а в третьем направлении (по оси z.) существенно меньше размеров тела. Отвод тепла в тело осуществляется за счет теплопроводности в направлении z. За расчетную величину принимается теплота источника, отнесенная к площади поперечного сечения -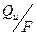

Реальный объемный ИТ – источник у которого размеры во всех направлениях (x,y,z) соизмеримы, а распределение теплоты в источнике не оказывает влияние на температурное поле тела на больших расстояниях от него.