Признаки постоянства. возраст. и убыв. ф-ции
Теорема13. Для того чтобы дифференцируемая наинтервале (a; b) функция f(x) возрастала (убывала) необходимо и достаточно, чтобы во всех его точках производная была неотрицательной, т. е. f’(x)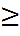 
0 (неположительной,f’(x) 
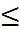0). Доказательство.Необходимость. Если функция f(x) возрастает на (a; b), то для любой точки x0 ∈ (a; b) при 
x > 0 имеем y = f(x0 + x) − f(x0) 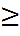0. Поэтому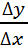 
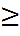0 и переходя к пределу при x → 0, получим f ’(x) 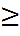0. Достаточность. Пусть a < x1 < x2 < b. Тогда, по формуле Лагранжа f(x2) − f(x1) = f’(ξ)(x2 − x1), где x1 < x2. Так как x2 − x1 > 0, то при f’(x) 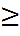0 на (a; b) (откуда следует, что, в частности, f’(ξ) 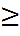0) будем иметь f(x1) 
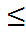f(x2) т. е. функция f(x) возрастает. Следствие 1. Если функция непрерывна на некотором интервале и имеет всюду в нём положительную (отрицательную) производную, кроме, быть может, конечного числа точек, в которых производная обращается в нуль или не существует, то функция строго возрастает (строго убывает). Доказательство непосредственно следует из теоремы 13: достаточно её последовательно применить ко всем промежуткам, на которые разбивается заданный интервал указанным конечным множеством точек.
44. Экстремум ф-ции.Теорема 14. Пусть x0 является точкой экстремума функции f(x), определённой в некоторой окрестности точки x0. Тогда либо производная f’(x0) не существует, либо f’(x0) = 0. оказательство. Действительно, если x0 является точкой экстремума для функции f(x), то найдётся такая окрестность V (x0), что значение функции f(x) в точке x0 будет наибольшим, или наименьшим на этой окрестности. Поэтому если в точке x0 существует производная, то она, согласно теореме Ферма равна нулю. геометрический смысл теоремы 14 заключается в следующем: в точках экстремума функции f(x) касательная к её графику параллельна оси абсцисс, если существует f’(x0) = 0; параллельна оси ординат, если f’(x0) бесконечна; существуют не совпадающие левая и правая касательные, если f’(x0 − 0)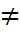 
f’(x0 + 0).Точки, в которых функция y = f(x) определена, а ее производная равна нулю, или не существует, называют критическими. Точки, в которых функция y = f(x) определена, а ее производная равна нулю, называют стационарными. Теорема 15 (Первый достаточный признак существования экстремума функции). Пусть x0 - критическая точка непрерывной функции f(x). Если f’(x) при переходе через точку x0 меняет знак с «+» на «-», то x0 - точка локального максимума; если f’(x) при переходе через точку x0 меняет знак с «-» на«+», то x0 - точка локального минимума; если f’(x) при переходе через точку x0 не меняет знак, то x0 не является точкой локального экстремума. Теорема 16 (Второй достаточный признак существования экстремума функции). Стационарная точка x0 функции f(x), дважды дифференцируемой в V (x0), является точкой локального минимума если f’’(x0) > 0, и точкой локального максимума, если f’’(x0) < 0. Теорема 17 (Третий достаточный признак существования экстремума функции).
Пусть функция f(x) n раз непрерывно дифференцируема в точке x0 и f’(x0) = f’’(x0) = . . . = f(n−1)(x0) = 0,f(n)(x0) 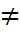0. Тогда: 1) если n - чётное и f(n)(x0) < 0, то x0 - точка локального максимума; 2) если n - чётное и f(n)(x0) > 0, то x0 - точка локального минимума;
3) если n - нечётное, то x0 - не является точкой локального экстремума.
Выпуклость функции
Определение 1. Функция f(x) называется выпуклой вниз (выпуклой) на интервале (a; b), если для любых x1 и x2 из
(a; b), a ≤ x1 < x2 ≤ b, хорда AB лежит не ниже графика этой функции, где A =(x1, f(x1)), B =(x2, f(x2)), т.е.
f(x1+t(x2−x1))≤f(x1)+t·(f(x2) − f(x1)), t ∈ [0; 1]. (5.28)
Определение 2. Функция f(x) называется выпуклой вверх (вогнутой) на интервале (a; b), если для любых x1 и x2 из
(a; b), a ≤ x1 < x2 ≤ b, хорда AB лежит не выше графика этой функции, т.е. если f(x1+t(x2−x1))≥f(x1)+t·(f(x2 −f(x1)), t∈[0; 1].
Теорема 18. Непрерывно дифференцируемая функция f(x) выпукла вниз на (a; b) тогда и только тогда, когда для любых x1 и x2 из (a; b) выполнено неравенство
f(x2) ≥ f(x1) + f’(x1)(x2 − x1) (5.29)
Доказательство. Необходимость. Из (5.28) имеем f(x1+t(x2−x1))−f(x1)t f(x2)−f(x1). В этом неравенстве перейдём к пределу при t → +0. Получим
lim t→+0f(x1 + t(x2 − x1))− f(x1)t= lim t→+0f(x1 + t(x2 − x1))− f(x1)t(x2 − x1)·(x2 − x1) = f’(x1)(x2 − x1) ≤ f(x2) − f(x1).
Достаточность. Пусть выполнено условие (5.29). Примем в нём x1 = x. Тогда f(x2) ≥ f(x) + f’(x)(x2 − x). (5.30)
Заменив в (5.30) x2 на x1, будем иметь f(x1)≥f(x)+f’(x)(x1−x). (5.31)
Умножив обе части неравенства (5.30) на t, а неравенства (5.31) на 1−t и сложив получившиеся при этом неравенства,
получим tf(x2) + (1 − t)f(x1) ≥ f(x) + f’(x)·(t(x2 − x1) + x1 – x).
Отсюда при x = x1 + t(x2 − x1) получим
f(tx2 + (1 − t)x1)≤tf(x2) + (1 − t)f(x1), t ∈ [0; 1], т.е. (5.28).
Аналогично доказываются необходимые и достаточные условия выпуклости вверх на интервале непрерывно дифференцируемой функции f(x).
Составим уравнение касательной к графику непрерывно дифференцируемой функции f(x) в точке x1: Y=f(x1)+f’(x1)(x−x1).
Тогда правая часть неравенства (5.29) есть Y (x2) и, значит, f(x2) > Y (x2). Отсюда и из теоремы 18 получаем:
Следствие 2. Непрерывно дифференцируемая функция f(x) выпукла вниз на (a; b) тогда и только тогда, когда все точки (x,f(x)), x ∈ (a; b), графика функции f(x) лежат не ниже касательной проведенной к нему в точке (x1, f(x1)), x1 ∈ (a; b).
Теорема 19 (достаточное условие выпуклости).
Если f(x) дважды непрерывно дифференцируема на интервале (a; b) и f’’(x)>0, ∀x∈(a;b), то на (a;b) функция f(x) выпукла вниз.
Если f’’(x)<0, ∀x∈(a;b), то на (a;b) функция f(x) выпукла вверх.
Доказательство. Пусть x1 - любая точка на (a; b). К графику функции f(x) в точке (x1, f(x1)) проведём касательную Y(x)=f(x1)+f’(x1)(x−x1).
Функцию f(x) разложим по формуле Тейлора
f(x) = f(x1) + f’(x1)(x − x1) + +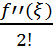 
(x − x1)2,
где ξ ∈ (x1; x).
Рассмотрим разность f(x) − Y (x) = 1
2f’’(ξ)(x − x1)2, которая представляет собой разность ординат кривой f(x) и касательной Y (x) в точке x. В силу непрерывности f’’(x), если f’’(x1) > 0, то и f’’(ξ) > 0 в достаточно малой окрестности V (x1) точки x1, а потому и f(x) − Y (x) > 0, ∀x ∈ V (x1).
Аналогично, если f’’(x1) < 0, то f(x) − Y (x) < 0, ∀x ∈ V (x1).
На основании следствия получаем, что в первом случае функция выпукла вниз, во втором - выпукла вверх.
Tочки перегиба
Определение 3. Точка x0 называется точкой перегиба функции f(x), если при переходе через точку x0 функция
меняет характер выпуклости.
Теорема 20 (необходимое условие точки перегиба). Если функция f(x) имеет непрерывную в точке x0 произ-
водную f’’(x) и x0 – точка перегиба, то f’’(x0) = 0.
Доказательство. Если бы в точке перегиба x0 выполнялось неравенство f’’(x0) > 0 или f’’(x0) < 0, то в силу непрерывности f’’(x) существовала бы окрестность точки x0, в которой f’’(x) > 0 или f’’(x) < 0. По теореме 19 в этой окрестности функция была бы выпукла вниз или вверх соответственно, что противоречит наличию перегиба в точке x0.
Из теоремы 20 следует, что точками возможного перегиба функции f(x) могут быть точки x0 в которых f’’(x0) = 0, либо точки, в которых f’’(x) не существует, в частности она бесконечна.
Теорема 21 (первое достаточное условие перегиба). Если функция f(x) дважды непрерывно дифференцируема в
окрестности точки x0 и при переходе через точку x0 производная f’’(x) меняет знак, то точка x0 является точкой
перегиба функции f(x).
Доказательство. Пусть, к примеру, f’’(x) > 0 при x < x0 и f’’(x)<0 при x>x0. Тогда по теореме 19 функция f(x) выпукла вниз на интервале (x; x0) и выпукла вверх на интервале (x0; x), т.е. x0 – точка перегиба.
Теорема 22 (общее достаточное условие перегиба). Пусть в точке x0 для функции f(x) выполнены условия
f’’(x0) = f’’’(x0) = . . . = f(n−1) (x0) = 0
и в точке x0 существует непрерывная производная f (x0), n > 2, причём f (x0) = 0. Если n – нечётное число, то
в точке x0 функция f(x) имеет перегиб.
Доказательство. Разлагая f(x) по формуле Тейлора n−1-го порядка с учетом условия получаем
f(x) = f(x0) + f’(x0)(x − x0) +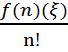 
(x − x0)n, (5.32)
где ξ расположена между x0 и x.
Если Y (x) = f(x0) + f’(x0)(x − x0) уравнение касательной к графику функции f(x) в точке (x0, f(x0)), то из (5.32) имеем
f(x) − Y (x) = 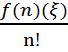(x − x0)n, (5.33) где n – нечётное.
В силу непрерывности f(n)(x) в точке x0 существует окрестность этой точки, в которой производная f(n)(x) сохраняет знак, совпадающий со знаком f(n)(x0). Поэтому можем считать, что знаки f(n)(x0) и f(n)(ξ) совпадают. Тогда из равенства (5.33) получаем, что при переходе x через x0 слева направо график функции располагается по разные стороны от касательной, т.е. в точке (x0, f(x0)) имеется перегиб.
47. Неопределенный интеграл. Определение 2. Совокупность F(x)+C всех первообразных функции f(x) на множестве X называется неопределенным интегралом и обозначается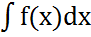 
= F(x) + C. (1.1) В формуле (1.1) f(x)dx называется подынтегральным выражением, f(x) – подынтегральной функцией, x – переменной интегрирования, а C – постоянной интегрирования. Св-ва. 10. Пусть функция f(x) имеет первообразную на числовом промежутке X. Тогда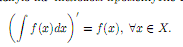 
20. Пусть функция F(x) дифференцируемая на числовом промежутке X. Тогда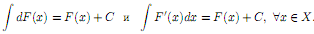 
30. Пусть функция f(x) интегрируема на числовом промежутке X, k - некоторое ненулевое действительное число. Тогда функция kf(x) имеет первообразную на числовом промежутке X и 