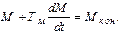С линейной мех-кой хар-кой

Преобразуем уравнение движения М – М_с = Jdω/dt: (5.12)

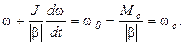(5.13)

Правая часть уравнения представляет собою скорость w_с, соответствующую моменту сопротивления М_С, однако, в рассматриваемом случае w₀ , а значит и w_с не постоянные величины, а известные функции времени w₀(t) и w_c(t). Т.о., уравнение (5.13) имеет вид:

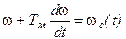. (5.14)

Решение этого дифференциального уравнения определит искомую зависимость w(t).

Для получения зависимости М(t) удобно воспользоваться непосредственно уравнением движения (5.12), подставив в него производную найденной функции w(t):

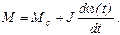(5.15)

Правая часть уравнения (5.14), вообще говоря, может иметь любой вид. Закон w₀(t) в случае безынерционного преобразователя формируется на его входе; при инерционном преобразователе закон w₀(t) связан со свойствами преобразователя. В ряде случаев закон w₀(t) формируется т.о., чтобы получить требуемый закон w(t).

3. Э-омагнитная постоянная времени, исследование ПП-сов с ее учетом.

(общий курс э-опривода Ильинский). ПП в э-оприводе с ДПТ незав. возбуждения при L_я¹ 0.

Длительность (Чекунов 90) протекания ПП-сов определяется соответствующими постоянными времени. Э-омагнитные ПП-сы обусловлены изменением запаса э-омагнитной энергии в электрических машинах, пропорциональных индуктивности их цепей и квадрату протекающего по ним тока. Длительность определяется индуктивностью обмоток.

Э-омагнитная инерция хар-ется э-омагнитной постоянной времени Т_э, (или Т_в), равной отношению индуктивностей L электрич. цепей привода к их активному сопротивлению:Т_э= L/R. Физический смысл э-омагнитной постоянной времени: это время, в течение которого ток в контуре, содержащем индуктивность, изменяется от нуля до установившегося значения, определяющегося величиной приложенного напряжения и омического сопротивления контура.

Пример. Если к зажимам обмотки, обладающей индуктивностью L­_В и омическим сопротивлением R­_В, приложить постоянное напряжение U­_В­, то уравнение ЭДС для цепи, например, обмотки возбуждения ДПТ выразится следующим образом:

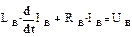
Разделив правую и левую части на R­_В, получим диф. уравнение первого порядка

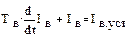
где: Т_В = L_в/R_в; (Т_в р + 1 = 0).

Решение уравнения для общего случая, когда при t = 0начальное значение тока i = I­_нач­:

i_в = i_в.уст(1 – е^-t/Тв) + i_в.нач е^-t/Тв

Т.о. закон изменения тока носит экспоненциальный хар-р. Продолжительность ПП-са приблизительно (3÷4)T­_В. Полученные уравнения не учитывают насыщение магнитной системы, т.е. считают L = const.

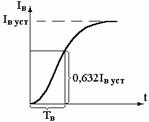
Рис.

Ориентировочно T­_В – двигателя независимого возбуждения

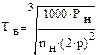, с.

При Р = (1 ÷ 100) кВт → T­_В­ = (0,1 ÷ 1) с

Р = (100 ÷ 1000) кВт → T­_В­ = (1 ÷ 2) с

Р = (1000 ÷ 3000) кВт → T­_В­ = (2 ÷ 4) с

Поэтому продолжительность нарастания тока может быть значительной (3÷4)T­_В , что приводит к уменьшению быстродействия. Для сокращения времени ПП-са применяют форсировку возбуждения – различные способы ускорения нарастания тока возбуждения.

Рассмотрим схему на рис.5.19 пуска ДПТ с индуктивностью L_я.

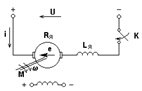
Рис. 5.19 – Схема пуска э-опривода ₌ I тока с двигателем независимого возбуждения

Для якорной цепи справедливо уравнение:

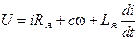, (5.23)

решив которое относительно w:

(*)

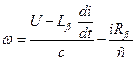и обозначив 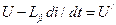получим . (**)

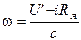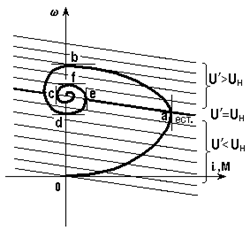
U¢ зависит от di/dt т.е. уравнение (**) представляет семейство прямых (рис.5.20,а), параллельных естественной хар-ке и располагающихся как ниже (di/dt > 0), так и выше

(di/dt < 0) нее. При di/dt = 0, очевидно, уравнение (**) соответствует естественной хар-ке.

После замыкания ключа К ток i начинает расти, значит растет М и привод разгоняется (для упрощения рассуждений примем М_с = 0), переходя при этом с хар-ки на на хар-ку

(di/dt > 0, но уменьшается по мере разгона). В процессе увеличения тока и скорости (участок 0а на рис.5.20) возрастает запас энергии как в индуктивности, так и во вращающемся якоре. В точке а рост тока прекращается; при этом в соответствии с (*) привод оказывается на естественной хар-ке, но М > М_с = 0. С точки а начинается спадание тока, т.е. энергия, запасенная в L_я, передается вращающемуся якорю. Механизм передачи очевиден из (*): напряжение, приложенное к якорю U¢, становится больше, чем напряжение сети U. На участке аb привод разгоняется, соответственно растет е = сw, причем в точке b i = 0 – запас энергии в L_я исчерпан, однако w >w₀ и e > U, т.е. в якоре запасена избыточная мех-кая энергия.

На участке bc под действием e > U ток изменяет направление, привод тормозится, при этом избыточная мех-кая энергия вновь переходит в э-омагнитную энергию, накапливаемую в индуктивности. В точке с di/dt = 0, однако в L_я запасена энергия, чему соответствует i ¹ 0 и

M ¹ 0. Привод продолжает тормозиться до точки d, затем процесс повторяется.

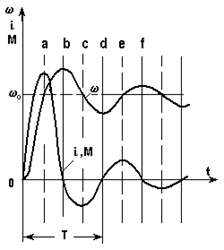
Кривая 0abcd... w₀ в плоскости w – M представляет собою динамическую мех-кую хар-ку. Соответствующие зависимости w(t), i(t) или M(t) показаны на рис. 5.20,б.

Колебательность процесса связана с тем, что происходит периодическое преобразование кинетиче­ской энергии в э-омагнитную и обратно. Т.к. в якорной цепи есть сопротивление R_я процесс перекачивания энергии сопровождается ее рассеиванием, вследствие чего система после ряда колебаний приходит в точку w₀, соответствующую установившемуся режиму.

а) б)

Рис. 5.20 – Мех-кие хар-ки (а) и ПП пуска при L_я ¹ 0 (б)

Если бы сопротивление R_я было равным нулю, колебания w и М имели бы незатухающий хар-р. Если, наоборот, R_я велико, энергии, запасенной в L_я на участке 0а, может оказаться недостаточно для покрытия потерь в R_я и вывода якоря в точку w > w₀ при i = 0. В этом случае процесс будет иметь апериодический хар-р. Для определения возможности колебательного процесса составляется хар-ристическое уравнение

1 + Т_мр + Т_мТ_яр² = 0 (из ур-я ω + Т_Мdω/dt +Т_МТ_Я d²ω/dt² = ω₀) (^D)

Определяются его корни p₁, p₂

→

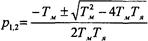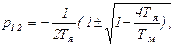
откуда вытекает условие колебательности процесса. Если

4Т_Я/Т_м > 1, т.е. Т_м < 4Т_я,

корни комплексные и процесс носит колебательный характер; если

4Т_Я/Т_м ≤ 1, т.е. Т_м ³ 4Т_я,

корни действительные и процесс апериодический.

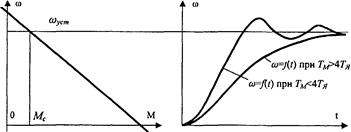
Рис.8.6 – Переходные хар-ки э-опривода с линейной мех-кой хар-кой при пуске

(elektroprivod Онищенко – 197стр)

Проведем (elektroprivod Онищенко – 191стр) анализ электромеханической системы, состоящей из двигателя с линейной механической характеристикой, и жест­кoгo механического звена. Движение такой электромеханической системы определяет­ся уравнением движения электропривода

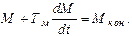(5.7)

Sssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssss

б) М_с = const, M линейно зависит от w, b < 0.

Пусть(общий курс эопривода Ильинский – 82стр) хар-ки двигателя и механизма имеют вид, представленный на рис.5.4 (увеличение скорости). Уравнение линейноймех-кой хар-ки двигателя с отрицательной жесткостью может быть записано как

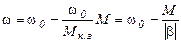(выразили из: М = β(ω₀ – ω) (5.4)

или

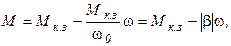(5.5)

где β = dM/dω – жесткость мех-кой хар-ки; для линейной хар-ки β = ΔM/Δω.

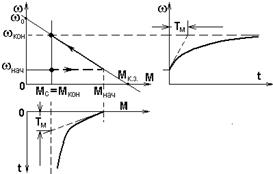
Рис. 5.4 – Мех-кие хар-ки и графики ПП-сов w(t) и M(t) при линейной зависимости w(М)

Подставив (5.5) в (5.1), после простых преобразований получим:

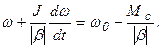
Выражение в правой части, как следует из (5.4), представляет собою w_кон. Обозначив коэффициент перед производной через Т_м, запишем:

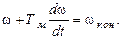(5.6)

Теперь подставим в (5.1) вместо dw/dt ее выражение, полученное из (5.4):

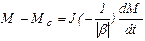
или, используя принятые выше обозначения,