Очно-заочная форма обучения.
| № п/п | Название раздела, темы | Кол-во часов дневной форме обучение | Лекций | Практика | Самостоятельная работа | Тестовые задания | Задания на контрольные работы | ||
| Аудит. | ДОТ | Аудит. | ДОТ | ||||||
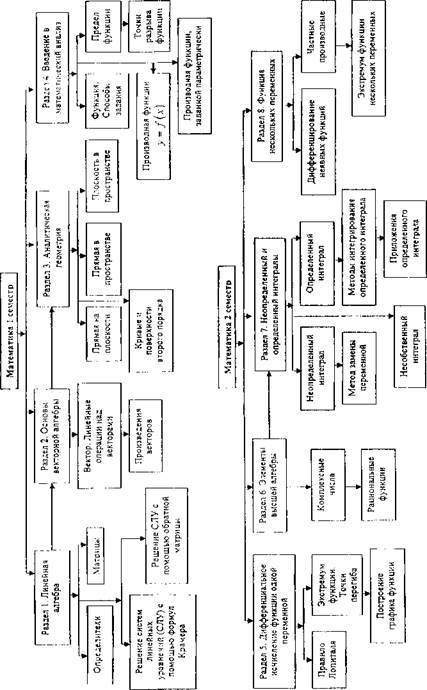
| Основы линейной алгебры | |||||||||
| 1.1 | Определитель второго порядка. Определитель третьего порядка. Определители высших порядков. Основные свойства определителей. | №1 №2 | |||||||
| 1.2 | Решение систем линейных уравнений. Формулы Крамера. | №3 №4 | |||||||
| 1.3 | Матрицы и их применение к решению систем линейных уравнений Обратная матрица. | №5 №6 | 1-я задача 1-ой к.р. | ||||||
| Основы векторной алгебры. Вектор. Линейные операции нал векторами Скалярное произведение векторов Смешанное произведение векторов. Векторное произведение векторов. | №7 №8 | 2-я задача 1-ой к.р. | |||||||
| Аналитическая геометрия | |||||||||
| 3.1 | Системы координат. | №9 №10 | |||||||
| 3.2 | Виды уравнений прямой на плоскости. Угол между прямыми на плоскости. | ||||||||
| 3.3 | Уравнения плоскости и прямой в пространстве. Угол между прямыми в пространстве. Угол между прямой и плоскостью в пространстве. Угол между плоскостями. | №11 №12 | 3-я задача 1-ой к.р. | ||||||
| 3.4 | Кривые второго порядка. Эллипс. Гипербола. Парабола. | №13 | 4-я задача 1-ой к.р. | ||||||
| 3.5 | Поверхности второго порядка. Эллипсоид. Однополостный гиперболоид. Двуполостный гиперболоид. Конус второго порядка. Эллиптический параболоид Циллиндры второго порядка. | №14 №15 | 5-я задача 1-ой к.р. | ||||||
| 4. | Введение в математический анализ. | ||||||||
| 4.1 | Функции и способы её задания. Элементарные функции. | №16 | |||||||
| 4.2 | Определение предела последовательности. Определение предела функции; простейшие свойства пределов; | №17 | |||||||
| 4.3 | Способы вычисления пределов. Сравнение бесконечно малых. | №18 №19 | 1-я задача 2-ой к.р. | ||||||
| 4.4 | Непрерывность функции в точке и на промежутке. Точки разрыва функции. | №20 | 2-я задача 2-ой к.р. | ||||||
| 4.5 | Производная функции. Производная суммы, произведения и частного функции. | №21 №22 | 3-я задача 2-ой к.р. | ||||||
| 4.6 | Дифференцирование сложной функции. Таблица производных. Дифференцирование функций заданных параметрически. | 4,5-я задача 2-ой к.р. | |||||||
| 5. | Дифференциальное исчисление функций одной переменной. | ||||||||
| 5.1 | Основные теоремы о дифференцируемых функциях. Правило Лопиталля. | 1-я задача 3-ой к.р. | |||||||
| 5.2 | Применение производной для исследования функций. Выпуклость и точки перегиба. Асимптоты графика функции. Общий план исследования функций. | 2-я задача 3-ой к.р. | |||||||
| 6. | Элементы высшей алгебры. | ||||||||
| 6.1 | Комплексные числа действия над ними. | №23 №24 | |||||||
| 6.2 | Многочлены. Основная терема алгебры. | ||||||||
| 7. | Неопределённый и определённый интегралы. | ||||||||
| 7.1 | Первообразная. Неопределённый интеграл и его свойства. Использование таблиц интегралов для непосредственного интегрирования. | №25 | 3-я задача 3-ой к.р. | ||||||
| 7.2 | Замена переменной в неопределённом интеграле. Формула интегрирования по частям. | №26 №27 | 4-я задача 3-ой к.р. | ||||||
| 7.3 | Определённый интеграл, его свойства и приложения. Формула Ньютона-Лейбница. | №28 №29 | 5-я задача 3-ой к.р. | ||||||
| 7.4 | Несобственные интегралы с бесконечными пределами и от неограниченных функций, их свойств. | 1.2-я задача 4-ой к.р. | |||||||
| 8. | Функция нескольких переменных | ||||||||
| 8.1 | Функция нескольких переменных. Область определения. Частные производные. Полный дифференциал. Дифференцирование неявных функций. | №30 №31№32 | 3.4-я задача 4-ой к.р. | ||||||
| 8.2 | Экстремумы функций нескольких переменных. | 5-я задача 4-ой к.р. |