Оценка качества движения в кривых
При движении на криволинейном участке пути сумма сил крипа и сил взаимодействия гребня колеса с рельсом уравновешивает боковые силы инерции, действующие на экипаж. Если равнодействующая сила взаимодействия гребня колеса и головки рельса превысит определенную величину, то колесо может приподняться над головкой рельса, и возникнет опасность схода колесной пары. Сход колеса с рельсов зависит от многих факторов, таких как угол набегания колесной пары, угол наклона гребня, коэффициент трения между колесом и рельсом, неподрессоренная масса колесной пары, нагрузка на ось, а также жесткость железнодорожного пути. В связи с этим, для оценки стремления колеса остаться в рельсовой колее обычно вводится интегральный показатель — коэффициент запаса устойчивости от схода колеса с рельса, для вычисления которого используется формула:
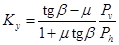 ,
,
где 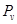 — вертикальная сила, действующая от колеса на путь;
— вертикальная сила, действующая от колеса на путь;
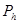 — поперечная сила, действующая от колеса на путь;
— поперечная сила, действующая от колеса на путь;
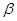 — угол наклона поверхности гребня к горизонтали;
— угол наклона поверхности гребня к горизонтали;
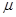 — коэффициент трения поверхностей колес и рельсов.
— коэффициент трения поверхностей колес и рельсов.
Оценка коэффициента запаса устойчивости от схода колеса с рельса должна производиться для движения с различными скоростями в круговых и переходных кривых с неровностями. Сочетание параметров кривых и неровностей выбирается таким образом, чтобы создать ситуацию, в которой возможен сход вагона с рельсов, и обычно определяется нормативными документами. При этом на кузов вагона может действовать сила ветра и продольные сжимающие или растягивающие нагрузки через сцепные устройства, которые вызывают опрокидывание вагона наружу или внутрь кривой.
Результатом численного интегрирования уравнений движения являются дискретные функции вертикальной и горизонтальной силы, действующей от колеса на рельс, по которым определяется временная зависимость коэффициента запаса устойчивости от схода колеса с рельса.
2.2 Нелинейный элемент связи «колесо – рельс»
В программном комплексе MEDYNA модели рельсовых экипажей состоят из твердых тел и связей между ними. В рамках этого подхода разработан элемент связи, который описывает контактное взаимодействие между колесом и рельсом или роликом (рис. 2).
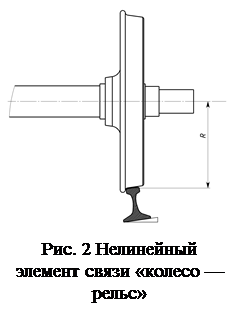 Нелинейный элемент соединяет два твердых тела: колесо и участок пути (который считается движущимся вместе с рельсовым экипажем) или ролик, или отсчетную систему координат (жесткий путь). Таким образом, пользователь может смоделировать:
Нелинейный элемент соединяет два твердых тела: колесо и участок пути (который считается движущимся вместе с рельсовым экипажем) или ролик, или отсчетную систему координат (жесткий путь). Таким образом, пользователь может смоделировать:
- жесткую колесную пару заданием одного твердого тела (колесной пары) и двух элементов связи «колесо – рельс» (одного для правого колеса и одного для левого);
- колесную пару с податливой осью заданием двух твердых тел (правое и левое колеса), соединенных упругим элементом (осью), и двух элементов связи «колесо – рельс»;
- независимое вращение колес;
- упругое колесо.
В нелинейном элементе связи «колесо – рельс» тела колеса и рельса имеют профилированные поверхности контакта, по которым они могут скользить друг относительно друга. При этом положение и форма пятна контакта, а также коэффициенты крипа вычисляются в каждый момент времени (или на каждой итерации). В зависимости от взаимного положения колеса и рельса, а также от формы профилей может возникать многоточечный контакт, при этом нет ограничения на число контактных пятен. Основное преимущество этого метода в том, что нормальная реакция в пятне контакта вычисляется не из уравнений кинематических связей, а по упругой деформации, возникающей в пятне контакта.
Для вычисления нелинейных зависимостей сил крипа от относительных проскальзываний в точках контакта существует несколько алгоритмов:
- Калкера с итерационным вычислением нормальных усилий;
- Вермюлена-Джонсона с аппроксимацией нормальных усилий и учетом крипа спина.
Для получения достоверных результатов используемая модель экипажа должна учитывать все нелинейности статических характеристик элементов связи.
При использовании нелинейного элемента связи «колесо – рельс» могут быть решены следующие задачи динамики рельсовых экипажей:
- оценка качества стационарного движения в круговых кривых;
- оценка износов колес и рельсов при движении в круговых кривых.
Оценка качества стационарного движения в кривой производится по коэффициенту запаса устойчивости от схода колеса с рельса (аналогично модели с подструктурой), но учет нелинейной контактной механики позволяет получить его уточненное значение. Для задачи оценки износов колес и рельсов (по мощности энергии, рассеянной в пятне контакта) моделирование пятна контакта с учетом всех нелинейностей особенно актуально.
При исследовании стационарного движения в круговых кривых используется метод определения квазистатического положения равновесия экипажа для заданной конфигурации и внешних нагрузок (ветровой, центробежной или действующей через сцепные устройства). При этом центробежные нагрузки на различные элементы экипажа рассчитываются в зависимости от радиуса кривой, возвышения наружного рельса и скорости движения. Для заданных внешних нагрузок с учетом нелинейной кинематики методом Ньютона-Рафсона вычисляется новое положение равновесия относительно исходного (для этого не надо описывать систему в различных отчетных системах координат).
2.3 Квазилинейный элемент связи «колесо – рельс»
В рамках программного комплекса MEDYNA также разработан квазилинейный элемент связи, который описывает контактное взаимодействие между колесом и рельсом или роликом (рис. 3). Аналогично нелинейному элементу он позволяет моделировать жесткую или упругую колесную пару, а также раздельное вращение колес при движении по упругому или жесткому пути.
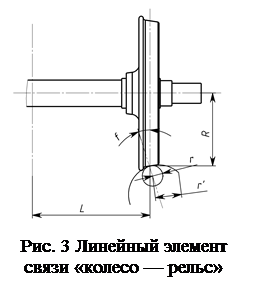 В квазилинейном элементе связи «колесо – рельс» нелинейные функции, описывающие геометрию контактного взаимодействия, аппроксимируются тремя постоянными параметрами. Это могут быть «стандартные» параметры, которые представляют собой коэффициенты гармонической линеаризации зависимостей угла боковой качки, угла контакта и разности радиусов кругов катания как функций поперечного смещения колесной пары. Эти параметры могут быть вычислены по таблично заданным функциям профилей методом квазилинеаризации для ожидаемого значения амплитуды поперечных колебаний колесной пары. Также могут использоваться параметры Жоли для аппроксимации профилей контактирующих поверхностей колеса и рельса окружностями: радиус кривизны профиля колеса и рельса в поперечном направлении в окрестности круга катания и угол наклона нормали в точке контакта в исходной конфигурации.
В квазилинейном элементе связи «колесо – рельс» нелинейные функции, описывающие геометрию контактного взаимодействия, аппроксимируются тремя постоянными параметрами. Это могут быть «стандартные» параметры, которые представляют собой коэффициенты гармонической линеаризации зависимостей угла боковой качки, угла контакта и разности радиусов кругов катания как функций поперечного смещения колесной пары. Эти параметры могут быть вычислены по таблично заданным функциям профилей методом квазилинеаризации для ожидаемого значения амплитуды поперечных колебаний колесной пары. Также могут использоваться параметры Жоли для аппроксимации профилей контактирующих поверхностей колеса и рельса окружностями: радиус кривизны профиля колеса и рельса в поперечном направлении в окрестности круга катания и угол наклона нормали в точке контакта в исходной конфигурации.
Зависимости сил крипа от относительных проскальзываний в точках контакта, определяемые по упрощенной нелинейной теории Калкера, также линеаризуются. Корректно построенная модель экипажа должна учитывать линеаризованные характеристики элементов связи.
При использовании линейного элемента связи «колесо – рельс» могут быть решены следующие задачи динамики рельсовых экипажей:
- оценка критической скорости;
- оценка качества стационарного движения в прямой;
- оценка степени демпфирования форм колебаний.
