Тема:Применение метода наименьших квадратов (МНК) для построения однофакторных нелинейных математических моделейвMS Excel, MathCAD, SMathStudio
| Вариант № 1, 21, 41 | Вариант № 2, 22, 42 | Вариант № 3, 23, 43 |
| Фактор Х | Результат эксперимента или статистический результат У | Фактор Х | Результат эксперимента или статистический результат У | Фактор Х | Результат эксперимента или статистический результат У |
| | 4,7 | | | | 3,0 |
| | 15,2 | | | | 0,5 |
| | 32,7 | | | | 0,3 |
| | 57,2 | | | | 0,7 |
| | 88,7 | | | | 1,0 |
| | 127,2 | | | | 1,1 |
| | 172,7 | | | | 1,2 |
| | 225,2 | | | | 1,3 |
| | 284,7 | | | | 1,4 |
| Вариант № 4, 24, 44 | Вариант № 5, 25, 45 | Вариант № 6, 26, 46 |
| Фактор Х | Результат эксперимента или статистический результат У | Фактор Х | Результат эксперимента или статистический результат У | Фактор Х | Результат эксперимента или статистический результат У |
| | | | 6,0 | | 7,20 |
| | | | 1,0 | | 10,20 |
| | | | 0,6 | | 15,20 |
| | | | 1,5 | | 22,20 |
| | | | 2,0 | | 31,20 |
| | | | 2,3 | | 42,20 |
| | | | 2,5 | | 55,20 |
| | | | 2,7 | | 70,20 |
| | | | 2,8 | | 87,20 |
| Вариант № 7, 27, 47 | Вариант № 8, 28, 48 | Вариант № 9, 29, 49 |
| Фактор Х | Результат эксперимента или статистический результат У | Фактор Х | Результат эксперимента или статистический результат У | Фактор Х | Результат эксперимента или статистический результат У |
| | -6,0 | | 8,0 | | 0,90 |
| | -4,0 | | 2,0 | | 2,20 |
| | -3,3 | | 8,0 | | 8,90 |
| | -3,0 | | 22,0 | | 20,00 |
| | -2,8 | | 40,0 | | 40,30 |
| | -2,6 | | 62,0 | | 70,60 |
| | -2,5 | | 88,0 | | 112,70 |
| | -2,5 | | 118,0 | | 168,40 |
| | -2,4 | | 152,0 | | 239,50 |
| Вариант № 10, 30, 50 | Вариант № 11, 31, 51 | Вариант № 12, 32, 52 |
| Фактор Х | Результат эксперимента или статистический результат У | Фактор Х | Результат эксперимента или статистический результат У | Фактор Х | Результат эксперимента или статистический результат У |
| | 7,0 | | -11,0 | | 1,3 |
| | 9,5 | | -5,0 | | 2,6 |
| | 10,3 | | -3,0 | | 9,1 |
| | 10,7 | | -2,0 | | 18,2 |
| | 11,0 | | -1,4 | | 29,9 |
| | 11,1 | | -1,0 | | 44,2 |
| | 11,2 | | -0,7 | | 61,1 |
| | 11,3 | | -0,5 | | 80,6 |
| | 11,4 | | -0,3 | | 102,7 |
| Вариант № 13, 33, 53 | Вариант № 14, 34, 54 | Вариант № 15, 35, 55 |
| Фактор Х | Результат эксперимента или статистический результат У | Фактор Х | Результат эксперимента или статистический результат У | Фактор Х | Результат эксперимента или статистический результат У |
| | 95,60 | | 98,80 | | 5,50 |
| | 82,40 | | 90,40 | | 4,00 |
| | 60,40 | | 67,60 | | 1,50 |
| | 29,60 | | 23,20 | | 2,00 |
| | 10,00 | | 50,00 | | 6,50 |
| | 58,40 | | 159,20 | | 12,00 |
| | 115,60 | | 311,60 | | 18,50 |
| | 181,60 | | 514,40 | | 26,00 |
| | 256,40 | | 774,80 | | 34,50 |
| Вариант № 16, 36, 56 | Вариант № 17, 37, 57 | Вариант № 18, 38, 58 |
| Фактор Х | Результат эксперимента или статистический результат У | Фактор Х | Результат эксперимента или статистический результат У | Фактор Х | Результат эксперимента или статистический результат У |
| | 0,90 | | 1,80 | | 0,60 |
| | 2,10 | | 2,40 | | 1,65 |
| | 4,10 | | 7,40 | | 3,40 |
| | 6,90 | | 20,80 | | 4,28 |
| | 10,50 | | 45,00 | | 4,80 |
| | 14,90 | | 84,20 | | 5,15 |
| | 20,10 | | 137,60 | | 5,40 |
| | 26,10 | | 208,40 | | 5,59 |
| | 32,90 | | 299,80 | | 5,73 |
| Вариант № 19, 39, 59 | Вариант № 20, 40, 60 |
| Фактор Х | Результат эксперимента или статистический результат У | Фактор Х | Результат эксперимента или статистический результат У |
| | 20,50 | | 3,80 |
| | 53,50 | | 11,60 |
| | 108,50 | | 14,40 |
| | 185,50 | | 41,80 |
| | 284,50 | | 85,00 |
| | 405,50 | | 150,20 |
| | 548,50 | | 242,60 |
| | 713,50 | | 364,40 |
| | 900,50 | | 520,80 |
Практическая работа 4 «Математические модели, решаемые методами линейного программирования»
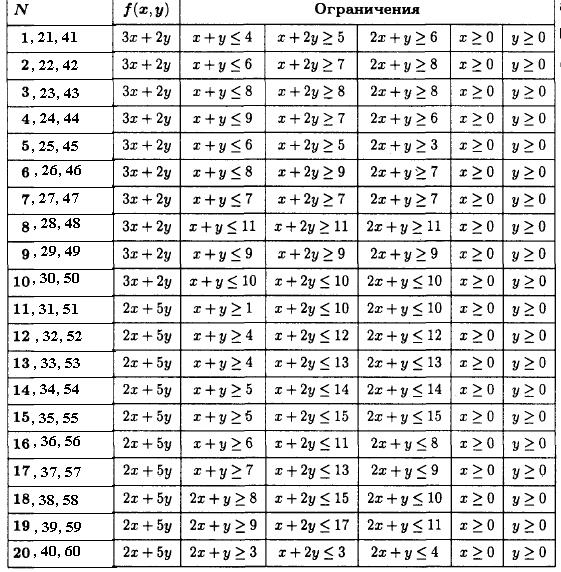
Решить задачу методом линейного программирования: найти минимум функции 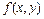 при заданных ограничениях (N – номер варианта)
при заданных ограничениях (N – номер варианта)
Практическая работа 5 по теме «Блок-схемы, алгоритмы, таблицы решений, аналитическая форма ММ»
| Варианты 1, 11, 21, 31, 41 и т.д. Разработать математическую модель и решить задачу: Требуется устроить прямоугольную площадку так, чтобы с трех сторон она была огорожена проволочной сеткой, а четвертой стороной примыкала к длинной каменной стене. Какова наибольшая по площади форма площадки, если имеется l погонных метров сетки? |
| Варианты 2, 12, 22, 32, 42 и т.д. Разработать математическую модель и решить задачу: Из квадратного листа картона со стороной а требуется сделать открытую прямоугольную коробку наибольшей вместимости, вырезав по углам квадраты и загнув выступы получившейся крестообразной фигуры. |
| Варианты 3, 13, 23, 33, 43 и т.д.. Разработать математическую модель и решить задачу: Открытый жестяной бак с квадратным основанием должен вмещать v литров. При каких размерах на изготовление бака потребуется наименьшее количество жести? |
| Варианты 4, 14, 24, 34, 44 и т.д. Разработать математическую модель и решить задачу: На прямолинейном отрезке АВ=а, соединяющем два источника света А (силы р) и В (силы к), найти точку М, освещаемую слабее всего (освещенность обратно пропорциональна квадрату расстояния от источника света). |
| Варианты 5, 15, 25, 35, 45 и т.д. Разработать математическую модель и решить задачу: Лампа висит над центром круглого стола радиуса r. При какой высоте лампы над столом освещенность предмета, лежащего на краю стола, будет наилучшая? (Освещенность прямо пропорциональна косинусу угла падения лучей света и обратно пропорциональна квадрату расстояния от источника). |
| Варианты 6, 16, 26, 36, 46 и т.д. Разработать математическую модель и решить задачу: Из круглого бревна диаметра d требуется вырезать балку прямоугольного сечения. Каковы должны быть ширина х и высота у этого сечения, чтобы балка оказывала наибольшее сопротивление на сжатие. (Сопротивление балки на сжатие пропорционально площади ее поперечного сечения). |
| Варианты 7, 17, 27, 37, 47 и т.д. Разработать математическую модель и решить задачу: Из круглого бревна диаметра d требуется вырезать балку прямоугольного сечения. Каковы должны быть ширина х и высота у этого сечения, чтобы балка оказывала наибольшее сопротивление на изгиб. (Сопротивление балки на изгиб пропорционально произведению ширины сечения на квадрат его высоты). |
| Варианты 8, 18, 28, 38, 48 и т.д. Разработать математическую модель и решить задачу: Из круглого бревна диаметра d требуется вырезать балку прямоугольного сечения. Каковы должны быть ширина х и высота у этого сечения, чтобы балка оказывала наименьшее сопротивление на сжатие. (Сопротивление балки на сжатие пропорционально площади ее поперечного сечения). |
| Варианты 9, 19, 29, 39, 49 и т.д. Разработать математическую модель и решить задачу: Из круглого бревна диаметра d требуется вырезать балку прямоугольного сечения. Каковы должны быть ширина х и высота у этого сечения, чтобы балка оказывала наименьшее сопротивление на изгиб. (Сопротивление балки на изгиб пропорционально произведению ширины сечения на квадрат его высоты). |
Варианты 10, 20, 30, 40, 50 и т.д. Разработать математическую модель и решить задачу: Определить, при каком диаметре у круглого отверстия в плотине секундный расход воды Q будет иметь наибольшее значение, если Q= 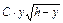 , h – глубина низшей точки отверстия (h и эмпирический коэффициент С – постоянны). , h – глубина низшей точки отверстия (h и эмпирический коэффициент С – постоянны). |
Практическая работа 6 по теме «Решение однокритериальных задач. Методы «сворачивания» множества критериев в одну целевую функцию»
Варианты нечетные (1, 3, 5 и т.д.): Определите лучший вариант из 3-х:
| Наименование Pi,j, ед. изм. х100000 | j=1 | j=2 | j=3 | li | opt |
| Величина запаса, м3 | 0,6 | 0,8 | 0,7 | 0,1 | max |
| Площадь неразработанной территории, м2 | 0,3 | 0,4 | 0,5 | 0,35 | min |
| Текущий объем добычи, м3 | | | | 0,25 | max |
| Маршрут на транспортировку нефти и газа, км | | | | 0,3 | min |
| Общие удельные затраты C j , руб. | | | | _ |
Варианты четные (2, 4, 6 и т.д.): Определите лучший вариант из 3-х:
| Наименование Pi,j, ед. изм. х100000 | j=1 | j=2 | j=3 | li | opt |
| Величина запаса, м3 | 0,7 | 0,65 | 0,71 | 0,2 | min |
| Площадь неразработанной территории, м2 | 0,55 | 0,49 | 0,51 | 0,3 | min |
| Текущий объем добычи, м3 | | | | 0,15 | max |
| Маршрут на транспортировку нефти и газа, км | | | | 0,35 | max |
| Общие удельные затраты C j , руб. | | | | _ |
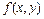 при заданных ограничениях (N – номер варианта)
при заданных ограничениях (N – номер варианта)
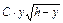 , h – глубина низшей точки отверстия (h и эмпирический коэффициент С – постоянны).
, h – глубина низшей точки отверстия (h и эмпирический коэффициент С – постоянны). 