Выбор шага интегрирования
Точность методов Эйлера и Рунге-Кутта существенно зависит от величины шага интегрирования h. Можно доказать [2], [3], что погрешность метода Эйлера имеет порядок h, а метода Рунге-Кутта – порядок  . Т. е. для достижения одной и той же точности в методе Эйлера нужно выбрать гораздо меньший шаг интегрирования, чем в методе Рунге-Кутта.
. Т. е. для достижения одной и той же точности в методе Эйлера нужно выбрать гораздо меньший шаг интегрирования, чем в методе Рунге-Кутта.
Рассмотрим подробнее процедуру выбора и уточнения шага интегрирования на примере метода Рунге-Кутта. Пусть 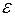 – заданная точность решения задачи Коши. Поскольку
– заданная точность решения задачи Коши. Поскольку  (где c=const), то начальное значение
(где c=const), то начальное значение  можно выбрать из неравенства
можно выбрать из неравенства
 (4.8)
(4.8)
При этом, чтобы попасть после n шагов интегрирования из точки a в точку b, необходимо одновременное выполнение условия:
 (целое число). (4.9)
(целое число). (4.9)
Кроме того, для подсчета погрешности метода Рунге-Кутта по формуле (4.7), нужно будет сделать просчет по формулам (4.5), (4.6) с шагом 2h. Поэтому необходимо также, чтобы отношение  было четным.
было четным.
После выбора начального значения шага  проводится его уточнение. Для этого из точки
проводится его уточнение. Для этого из точки 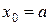 просчет по формулам (4.5), (4.6) выполняется дважды сначала с шагом h, а затем из той же точки с шагом 2h. При этом получаются два значения решения задачи (
просчет по формулам (4.5), (4.6) выполняется дважды сначала с шагом h, а затем из той же точки с шагом 2h. При этом получаются два значения решения задачи ( 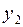 и
и  ) в одной и той же точке
) в одной и той же точке  . Если
. Если  , то
, то  можно выбрать в качестве шага интегрирования, иначе необходимо уменьшить h в два раза и повторить процедуру проверки.
можно выбрать в качестве шага интегрирования, иначе необходимо уменьшить h в два раза и повторить процедуру проверки.
Задание на лабораторную работу
1. Из табл. 4.1 выбрать свой вариант задания ( 
 ).
).
Таблица 4.1
Варианты заданий
| № |  | a | b |  | № |  | a | b |  |
 | 3,4 |  | 2,8 | ||||||
 | 3,8 |  | 4,4 | ||||||
 | 1,6 |  | 3,8 | ||||||
 | 3,2 |  | 2,6 | ||||||
 | 1,8 |  | 5,4 | ||||||
 | 5,4 |  | 3,6 | ||||||
 | 5,2 |  | 3,4 | ||||||
 | 1,8 |  | 3,8 | ||||||
 | 1,6 |  | 5,2 | ||||||
 | 6,4 | 0.5 |  | 4,6 | |||||
 | 1,6 |  | 2,8 | ||||||
 | 4,6 |  | 4,8 | ||||||
 | 1,8 |  | 2,6 | ||||||
 | 5,6 |  | 2,8 | ||||||
 | 4,6 |  | 0,6 | 2,2 |
2. Выбрав в качестве начального шага интегрирования  и
и  , решить задачу Коши на отрезке
, решить задачу Коши на отрезке 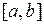 методом Эйлера и определить по формуле (4.4) относительную погрешность найденного решения.
методом Эйлера и определить по формуле (4.4) относительную погрешность найденного решения.
3. Выбрав в качестве начального шага интегрирования  , решить задачу Коши на отрезке
, решить задачу Коши на отрезке 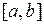 методом Рунге-Кутта.
методом Рунге-Кутта.
4. Построить на миллиметровой бумаге графики решений, найденных методами Эйлера и Рунге-Кутта.
5. Продолжить работу в компьютерном классе.
6. Выписать значения «точного решения», полученного на компьютере с помощью стандартной функции odesolve системы Mathcad, в промежуточных точках для 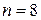 . Построить график решения по этим точкам.
. Построить график решения по этим точкам.
7. Используя найденные в п.6 значения, составить таблицу локальных абсолютных погрешностей решений, найденных методами Эйлера и Рунге-Кутта на МК.
8. Выписать автоматически полученные на компьютере в разделе «Метод Рунге-Кутта» значения решения задачи Коши на отрезке 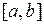 методом Рунге-Кутта с начальным шагом интегрирования
методом Рунге-Кутта с начальным шагом интегрирования  и, используя формулу (4.7), определить относительную погрешность данного решения.
и, используя формулу (4.7), определить относительную погрешность данного решения.
9. Оформить отчет по работе, в который входят: титульный лист; таблица с решением задачи Коши методом Эйлера с шагом  и
и  ; относительная погрешность найденного решения методом Эйлера; таблица с решением задачи Коши методом Рунге-Кутта с шагом
; относительная погрешность найденного решения методом Эйлера; таблица с решением задачи Коши методом Рунге-Кутта с шагом  ; полученное на компьютере точное решение задачи Коши; таблица абсолютных погрешностей решений, найденных методами Эйлера и Рунге-Кутта; абсолютные погрешности этих решений; таблица с компьютерным решением задачи Коши методом Рунге-Кутта с шагом
; полученное на компьютере точное решение задачи Коши; таблица абсолютных погрешностей решений, найденных методами Эйлера и Рунге-Кутта; абсолютные погрешности этих решений; таблица с компьютерным решением задачи Коши методом Рунге-Кутта с шагом  ; относительная погрешность найденного решения методом Рунге-Кутта.
; относительная погрешность найденного решения методом Рунге-Кутта.
