Статистические методы обработки
В случае исследования сложных систем используется большое количество реализаций N и в результате компьютерного моделирования получается большой объем информации о процессе работы системы. Для того, чтобы не пришлось запоминать всю информацию о состояниях моделируемой системы, нужно в процессе вычислений фиксировать и обрабатывать результаты моделирования таким образом, чтобы оценки искомых характеристик (параметров) формировались постепенно по ходу моделирования.
Если при моделировании процесса функционирования конкретной системы учитываются случайные факторы, то и среди результатов моделирования присутствуют случайные величины. В качестве оценок для искомых характеристик рассчитывают средние значения, дисперсии, корреляционные моменты и т. д.
Пусть в качестве искомой величины фигурирует вероятность некоторого события А. В качестве оценки для искомой вероятности p=P(A) используется частота наступления события m/N, где m – число случаев наступления события А; N – число реализаций.
Такая оценка вероятности появления события А является состоятельной, несмещенной и эффективной. В случае необходимости получения оценки вероятности в памяти компьютера при обработке результатов моделирования достаточно накапливать лишь число m (при условии, что N задано заранее).
Аналогично при обработке результатов моделирования можно подойти к оценке вероятностей возможных значений случайной величины, т. е. закона распределения. Область возможных значений случайной величины η разбивается на n интервалов. Затем накапливается количество попаданий случайной величины в эти интервалы mk, k=1,…,n.
Оценкой для вероятности попадания случайной величины в интервал с номером k служит величина mk/N. Таким образом, при этом достаточно фиксировать n значений mk при обработке результатов компьютерного моделирования.
Для оценки среднего значения случайной величины накапливается сумма возможных значений случайной величины yk, k=1,…, N, которые она принимает при различных реализациях. Тогда среднее значение

При этом ввиду несмещенности и состоятельности оценки

В качестве оценки дисперсии случайной величины η при обработке результатов моделирования можно использовать

Непосредственное вычисление дисперсии по этой формуле нерационально, так как среднее значение 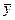 изменяется в процессе накопления значений yk. Это приводит к необходимости запоминания всех N значений yk. Поэтому более рационально организовать фиксацию результатов моделирования для оценки дисперсии с использованием выражения:
изменяется в процессе накопления значений yk. Это приводит к необходимости запоминания всех N значений yk. Поэтому более рационально организовать фиксацию результатов моделирования для оценки дисперсии с использованием выражения:

В этом случае для вычисления дисперсии достаточно накапливать только две частичные суммы: значений yk и квадратов этих значений  .
.
Корреляционный моментдвух случайных величин ξ и η, принимающих возможные значения xk и yk соответственно, будет равен:

Также для вычисления корреляционного момента используется следующее выражение:

которое требует запоминания в процессе моделирования небольшого количества значений.
Если при моделировании системы искомыми характеристиками являются математическое ожидание и корреляционная функция случайного процесса у(t) [в интервале моделирования (0,Т)], то для нахождения оценок этих величин указанный интервал разбивают на отрезки с постоянным шагом Δt и накапливают значения процесса yk(t) для фиксированных моментов времени t= tm=mΔt.
При обработке результатов моделирования математическое ожидание и корреляционную функцию можно представить в виде:

где u и z пробегают все значения tm.
Для уменьшения затрат ресурсов вычислительной системы на хранение промежуточных результатов последнее выражение также целесообразно привести к следующему виду:

Отметим особенности фиксации и обработки результатов моделирования, связанные с оценкой характеристик стационарных случайных процессов, обладающих эргодическим свойством.
Эргодическое свойствозаключается в следующем. Пусть рассматривается процесс у(t). Тогда с учетом этих предположений поступают в соответствии с правилом: среднее по времени равно среднему по множеству. Это означает, что для оценки искомых характеристик выбирается одна достаточно продолжительная реализация процесса у(t), для которой целесообразно фиксировать результаты моделирования. Для рассматриваемого случая запишем математическое ожидание и корреляционную функцию процесса:

На практике при моделировании системы на компьютере интервал (0,Т) оказывается ограниченным и, кроме того, значения у(t) удается определить только для конечного набора моментов времени tm. При обработке результатов моделирования для получения оценок 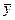 и В(τ) можно использовать приближенные формулы:
и В(τ) можно использовать приближенные формулы:

Именно эти выражения далее следует преобразовать к виду, позволяющему эффективно организовать порядок фиксации и обработки результатов моделирования.
