Расчет бесконечно длинной балки на упругом основании, загруженной одной силой Р

Наиболее просто решается задача об изгибе бесконечно длинной балки, нагруженной одной сосредоточенной силой (Рис.2). Помимо непосредственного практического значения решение этой задачи позволит путем последовательных приближений рассчитывать и балки конечной длины.

Рис.2. Расчетная схема балки бесконечной длины.

Начало координат расположим в точке приложения силы Р. Определим постоянные А, В, С и D. Так как вся реакция основания, равная силе Р должна быть конечной величиной, то прогибы балки в точках, бесконечно удаленных от точки приложения силы, должны обращаться в нуль:

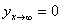(5)

При бесконечно больших значениях х два вторых слагаемых в правой части формулы (4) обращаются в нуль благодаря множителю 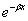, два же первых могут обратиться в нуль лишь при

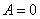и

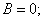
таким образом,

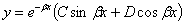(6)

Далее, по симметрии нагрузки и реакции основания, касательная к изогнутой оси в точке приложения силы должна идти параллельно оси абсцисс:

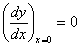
Дифференцируя (6), получаем:

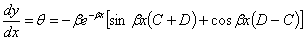
Подставляя в это выражение 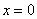и приравнивая результат нулю, находим:

D — С = 0 и C=D;

таким образом, уравнения будут:

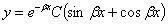	(7)
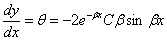	(8)

Для определения последней постоянной С имеем еще одно уравнение: нам известна величина поперечной силы в начале координат.

Разрезав балку сечением в точке О справа от силы Р и рассматривая правую часть балки, видим, что поперечная сита в этом сечении равна реакции основания, действующей на правую половину балки со знаком минус; так как реакция направлена вверх (для правой половины) и вся реакция основания равна Р, значит, поперечная сила в сечении при х = 0 равна

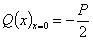
Но, с другой стороны

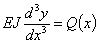(9)

Таким образом,

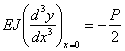(10)

Вычисляем, пользуясь (8), 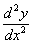и :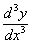

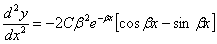	(11)
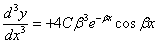	(12)

Подставляя (12) в (10) и приравнивая х нулю, получаем:

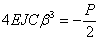и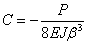

Теперь значения у и ее производных получают вид

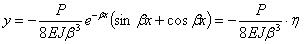
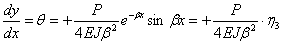
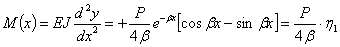
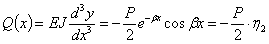
Таким образом, напряженное состояние и деформации балки на упругом основании всецело определяются нагрузкой и коэффициентом 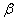, зависящим от соотношения жесткостей балки и упругого основания.

Лекция № 32. Энергетические методы расчета деформаций.

Постановка задачи.

Кроме рассмотренных способов вычисления прогибов и углов поворота сечений балок существует более общий метод, пригодный для определения деформаций любых упругих конструкций. Он основан на применении закона сохранения энергии.

При статическом растяжении или сжатии упругого стержня происходит превращение потенциальной энергии из одного вида в другой; часть потенциальной энергии действующего на стержень груза полностью переходит в потенциальную энергию деформации стержня. Действительно, если мы будем нагружать стержень путем постепенного подвешивания к его нижнему концу очень малых грузов dP, то при добавлении каждого такого груза подвешенная уже часть нагрузки опустится и ее потенциальная энергия уменьшится, а потенциальная энергия деформации стержня соответственно увеличится.

Это явление имеет место при любом виде деформации всякой упругой конструкции при статической нагрузке; такую конструкцию можно рассматривать как своеобразную машину, преобразующую один вид потенциальной энергии в другой.

Мы условились называть «статической» такую нагрузку, которая возрастает постепенно и таким образом, что ускорениями элементов конструкции можно пренебречь; передача давлений (сил) от одной части конструкции на другую не меняет характера движения, этих частей, т. е. их скорость остается постоянной и ускорение отсутствует.

При этих условиях деформация конструкции не будет сопровождаться изменением кинетической энергии системы, и будет иметь место лишь преобразование потенциальной энергии из одного вида в другой. При этом мы пренебрегаем магнитными, электрическими и тепловыми явлениями, сопровождающими упругие статические деформации тела лишь в очень слабой мере.

Так как характер движения всех элементов конструкции с течением времени не меняется, то в каждый момент времени будет иметь место равновесие как для каждой части конструкции в целом под действием внешних сил и реакций, так и для каждого элемента этой части под действием внешних сил и напряжений, приложенных к этому элементу. Деформации конструкции, напряжения в ее частях и реакции, передающиеся от одной части на другую, успевают следовать за ростом нагрузки.

Таким образом, можно сказать, что полное преобразование одного вида потенциальной энергии в другой имеет место, если деформация происходит без нарушения равновесия системы. Мерой энергии, превратившейся в другой вид, является величина работы, произведенной силами, действующими на конструкцию.

Обозначим величину накопленной потенциальной энергии деформации через U, а уменьшение потенциальной энергии внешних нагрузок 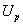. Тогда величина 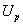измеряется положительной работой этих нагрузок 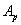, с другой стороны, накоплению потенциальной энергии деформации U соответствует отрицательная работа внутренних, междучастичных сил А, так как перемещения точек тела при деформации происходят в обратном по отношению к внутренним силам направлении.

Закон сохранения энергии при деформациях упругих систем принимает вид:

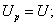
заменяя в этой формуле величины 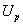и U численно равными им значениями работ 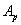и —А, получаем иную формулировку этого закона:

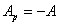или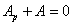

Эта формулировка закона сохранения энергии совпадает с так зазываемым «началом» возможных перемещений в применении к упругим системам. Последнее равенство выражает, что при перемещениях без нарушения равновесия сумма работ всех сил, приложенных к точкам тела, равна нулю.

Таким образом, начало возможных перемещений в применении к упругим системам является следствием закона сохранения энергии.

Таким образом, потенциальная энергия деформации 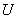численно равна работе внешних сил 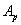, проделанной ими этой деформации: