МКЭ – инженерный подход
До сих пор мы знакомились с МКЭ как с проекционным методом со специальными координатными функциями. Полезно, особенно с практической, алгоритмической стороны и для понимания сути метода, познакомиться с подходом инженеров. Широкое использование при этом матричного формализма удобно при проведении конкретных вычислений.
Для иллюстрации инженерного подхода рассмотрим пример задачи о растяжении – сжатии стержня постоянного поперечного сечения под действием сил собственного веса (рис.7). Чтобы не вводить краевых задач с новыми краевыми условиями, будем считать, что концы стержня закреплены (В. П. Суслов и др. Строительная механика корабля и теория упругости. Л.: Изд. ЛКИ, 1972).
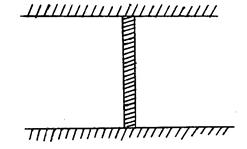
Рис.7. Стержень с закрепленными концами
Математически эта задача формулируется в виде краевой задачи (1.4), (1.5) при 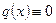 ,
, 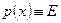 ,
, 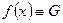 :
:
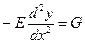 ,
, 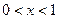 ,
,
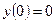 ,
, 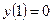 ,
,
где 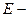 модуль Юнга,
модуль Юнга, 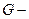 приведенная объемная сила. Эквивалентная задача о минимуме квадратичного функционала представляет собой формулировку принципа минимума потенциальной энергии.
приведенная объемная сила. Эквивалентная задача о минимуме квадратичного функционала представляет собой формулировку принципа минимума потенциальной энергии.
Будем решать эту задачу приближенно. Разобьем стержень точками 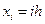 на
на 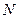 конечных элементов равной длины
конечных элементов равной длины 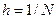 и будем считать, что на каждом элементе
и будем считать, что на каждом элементе 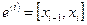 приближенное решение представляется линейной функцией. Поэтому для определения приближенного решения на
приближенное решение представляется линейной функцией. Поэтому для определения приближенного решения на 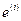 его достаточно знать в двух точках. Пусть эти точки – концы элемента, т.е. узлы
его достаточно знать в двух точках. Пусть эти точки – концы элемента, т.е. узлы 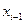 ,
, 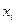 . Обозначим приближенное решение через
. Обозначим приближенное решение через 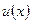 , его значения на концах – через
, его значения на концах – через 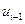 и
и 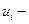 узловые значения.
узловые значения.
Очевидно, что
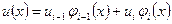 ,
, 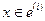 , (1.38)
, (1.38)
где
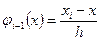 ,
, 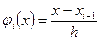 ,
,
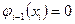 ,
, 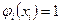 ,
,
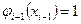 ,
, 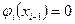 ;
;
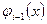 ,
, 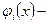 называются функциями формы конечного элемента.
называются функциями формы конечного элемента.
Пусть
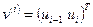 ,
, 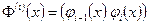
соответственно матрица-столбец и матрица-строка. Тогда соотношение (1.38) может быть записано в виде
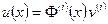 ,
, 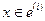 . (1.39)
. (1.39)
Подставим приближенное решение 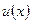 в функционал удвоенной потенциальной энергии
в функционал удвоенной потенциальной энергии
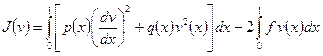 .
.
Для этого представим его сначала в виде суммы функционалов, каждый из которых определен на своем элементе. Тогда
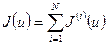 . (1.40)
. (1.40)
С учетом того, что 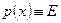 ,
, 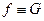 ,
,
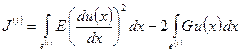 . (1.41)
. (1.41)
Учитывая (1.38), (1.39), продольную деформацию 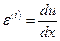 и нормальное напряжение
и нормальное напряжение 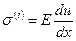 представим в виде
представим в виде
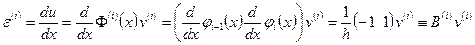 ,
,
где
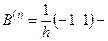 матрица строка,
матрица строка, 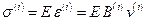 .
.
Введем в рассмотрение 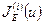 :
:
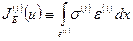 .
.
Тогда
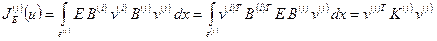 ,
,
где
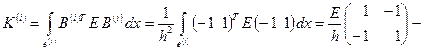 матрица жесткости элемента.
матрица жесткости элемента.
Далее, так как
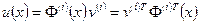 ,
,
то
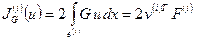 ,
,
где 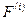 определяется следующим образом:
определяется следующим образом:
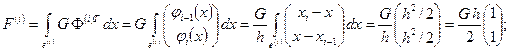
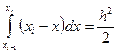 ;
;
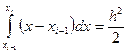 .
.
Вектор 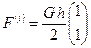 называется вектором узловых сил элемента.
называется вектором узловых сил элемента.
Таким образом, удвоенная потенциальная энергия элемента записывается в виде
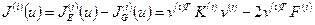 . (1.42)
. (1.42)
Она представляет собой квадратичную форму узловых значений элемента.
Подставим (1.42) в (1.40), получим
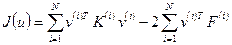 . (1.43)
. (1.43)
Очевидно, что правая часть равенства (1.43) представляет собой квадратичную форму совокупности всех узловых значений на промежутке  .
.
Между полным вектором неизвестных
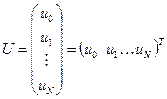 ,
,
и вектором неизвестных 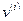 на элементе
на элементе 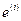 имеется вполне очевидная связь:
имеется вполне очевидная связь:
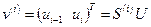 , (1.44)
, (1.44)
где 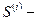 матрица порядка
матрица порядка 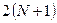 следующего вида:
следующего вида:
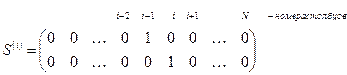
Справедливость этого равенства проверяется непосредственно. Матрица 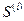 называется матрицей кинематических связей.
называется матрицей кинематических связей.
Используя (1.44), перепишем (1.43) следующим образом:
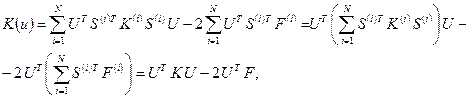
где через 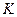 и
и 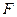 обозначены:
обозначены:
- глобальная матрица жесткости
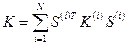 , (1.45)
, (1.45)
- глобальный вектор нагрузки
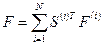 . (1.46)
. (1.46)
Таким образом, удвоенная потенциальная энергия стержня на приближенном решении записывается в виде
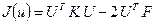 . (1.47)
. (1.47)
Отсюда следует, что на приближенном решении значение потенциальной энергии есть функция 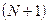 переменной
переменной 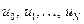 , условием минимума которой является обращение в нуль производных первого порядка по переменным
, условием минимума которой является обращение в нуль производных первого порядка по переменным 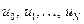 .
.
Проведя дифференцирование и приравняв полученные выражения для производных к нулю после сокращения на множитель 2, получим систему уравнений
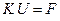 . (1.48)
. (1.48)
Действительно, пусть
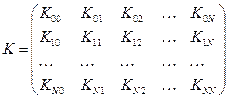 ,
,  .
.
Тогда
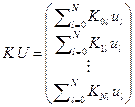 ,
,
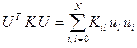 ,
,
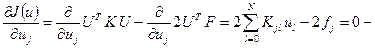
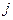 -строка системы (1.48), умноженная на 2.
-строка системы (1.48), умноженная на 2.
Здесь следует сделать важную оговорку. Система (1.48) не дает приближенное решение нашей задачи. Дело в том, что во всех рассуждениях мы считали все узлы равноправными, поэтому оказались не учтенными условия закрепления на концах промежутка (стержня). Чтобы их учесть, нужно положить 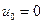 ,
, 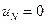 и заменить этими уравнениями первое и последние уравнения системы (1.48). Эти два уравнения системы (1.48) представляют собой условия свободного конца – естественные условия по нашей терминологии. После такой замены получаем искомую систему уравнений.
и заменить этими уравнениями первое и последние уравнения системы (1.48). Эти два уравнения системы (1.48) представляют собой условия свободного конца – естественные условия по нашей терминологии. После такой замены получаем искомую систему уравнений.
Можно вообще исключить 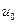 и
и 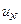 из системы, после чего получим систему относительно
из системы, после чего получим систему относительно 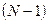 неизвестных значений с симметричной матрицей. Обозначим ее
неизвестных значений с симметричной матрицей. Обозначим ее 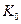 и пусть
и пусть
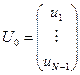 ,
, 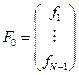 .
.
Тогда система запишется в виде
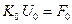 . (1.49)
. (1.49)
Следует отметить, что система (1.49) совпадает с системой (1.25) при 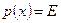 ,
, 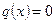 ,
, 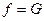 , которая ранее в матричной форме была записана в виде
, которая ранее в матричной форме была записана в виде
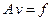 .
.
Отметим также, что
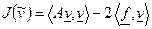 .
.
Таким образом, мы изложили два подхода к построению одной и той же системы сеточных уравнений МКЭ.
Второй, инженерный подход важен при реальных вычислениях в алгоритмическом отношении. При этом следует отметить, что на практике при вычислении глобальных матриц жесткости 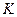 и вектора нагрузки
и вектора нагрузки 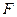 вовсе не обязательно выполнять перемножения матриц и умножения матриц на векторы, которые предписываются формулами (1.45) и (1.46).
вовсе не обязательно выполнять перемножения матриц и умножения матриц на векторы, которые предписываются формулами (1.45) и (1.46).
Это объясняется простотой структуры матрицы 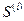 . Проиллюстрируем процесс вычисления
. Проиллюстрируем процесс вычисления 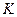 и
и 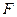 на примере при
на примере при 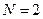 .
.
Имеем
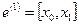 ,
, 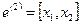 ,
,
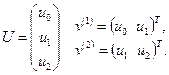
Матрицы кинематических связей, сопоставляющие вектору 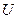 векторы
векторы 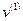 и
и 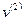 , очевидно имеют вид
, очевидно имеют вид
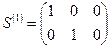 ,
, 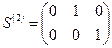 .
.
Таким образом:
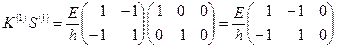 ;
;
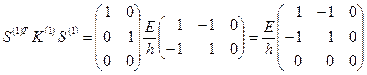 ;
;
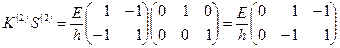 ;
;
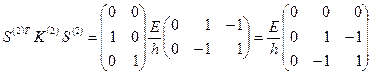 ;
;
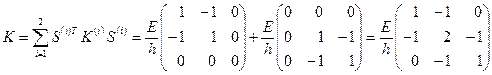 ;
;
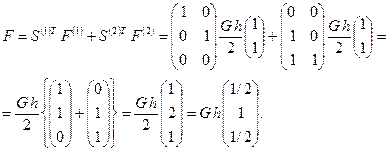
Из приведенных формул следует, что умножение 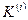 на
на 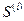 и
и 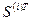 сводится к соответствующему окаймлению нулевыми строками и столбцами с сохранением симметрии. Соответственно изменяется вектор
сводится к соответствующему окаймлению нулевыми строками и столбцами с сохранением симметрии. Соответственно изменяется вектор 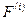 при умножении слева на матрицу
при умножении слева на матрицу 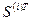 . Эти наблюдения и позволяют осуществлять сборку матриц
. Эти наблюдения и позволяют осуществлять сборку матриц 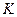 и
и 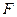 . Именно так она осуществляется при реализации соответствующих алгоритмов.
. Именно так она осуществляется при реализации соответствующих алгоритмов.
Сходимость МКЭ
Весьма важной характеристикой для вычислительной практики любого приближенного метода является скорость стремления к нулю погрешности метода. Поясним подробнее.
Пусть 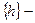 семейство шагов сетки и пусть
семейство шагов сетки и пусть 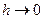 . Например, при
. Например, при 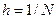 ,
, 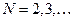 мы будем иметь последовательность шагов сетки. Пусть каждому значению
мы будем иметь последовательность шагов сетки. Пусть каждому значению 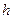 соответствует сеточное решение, полученное методом сеток или МКЭ. Обычно в методе сеток под погрешностью метода имеют в виду величину
соответствует сеточное решение, полученное методом сеток или МКЭ. Обычно в методе сеток под погрешностью метода имеют в виду величину 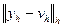 , где
, где 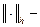 некоторая сеточная норма;
некоторая сеточная норма; 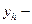 сеточная функция, построенная по точному решению
сеточная функция, построенная по точному решению 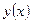 ;
; 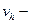 приближенное решение, построенное методом сеток. Обычно
приближенное решение, построенное методом сеток. Обычно 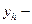 это значения точного решения в узлах сетки.
это значения точного решения в узлах сетки.
Говорят, что метод сеток сходится, если
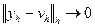 при
при 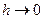 .
.
Приведем примеры сеточных норм. Сеточная норма
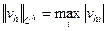
является аналогом нормы пространства непрерывных функций, сеточная норма
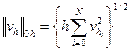
является аналогом нормы в пространстве 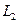 .
.
Если для всех 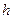 , меньших некоторого
, меньших некоторого 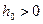 ,
, 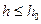 , выполняется неравенство
, выполняется неравенство
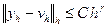 ,
, 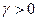 ,
,
где постоянная 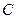 не зависит от
не зависит от 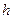 , то говорят, что метод сеток сходится со скоростью
, то говорят, что метод сеток сходится со скоростью 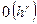 .
.
Под сходимостью методов Ритца и Галеркина, а следовательно, и МКЭ, естественно понимать тот факт, что последовательность приближенных решений – функций 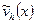 – сходится к точному решению в некоторой норме при
– сходится к точному решению в некоторой норме при 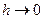 , т.е. что погрешность
, т.е. что погрешность
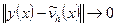 при
при 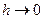 .
.
Если при всех 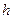 , меньших некоторого
, меньших некоторого 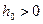 , имеет место неравенство
, имеет место неравенство
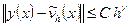 ,
, 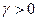 ,
,
где постоянная 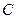 не зависит от
не зависит от 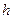 , то говорят, что МКЭ сходится со скоростью
, то говорят, что МКЭ сходится со скоростью 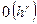 .
.
Отличие в подходе к вопросу о сходимости метода сеток и МКЭ связано с тем, что в методе сеток искомой является сеточная функция, тогда как в МКЭ приближенное решение – это функция, имеющая ту же область задания, что и точное решение.
Обратимся вновь к краевой задаче (1.4), (1.5). Докажем, что приближенное решение 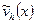 , построенное МКЭ, сходится к точному.
, построенное МКЭ, сходится к точному.
Приближенное решение является решением следующей вариационной задачи:
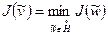 ;
;
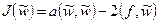 .
.
Путем интегрирования по частям легко показать, что
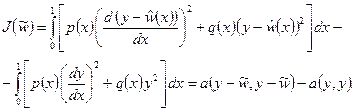
Так как  не зависит от
не зависит от  , то
, то 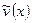 будет еще и решением такой задачи на минимум:
будет еще и решением такой задачи на минимум:
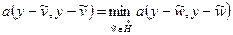 . (1.50)
. (1.50)
Это очень важное соотношение. Используя введенную ранее в параграфе 1.5 энергетическую норму
|| 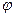 ||
|| 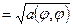 ,
,
перепишем (1.50) в виде
|| 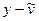 ||
|| 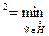 ||
|| 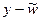 ||
|| 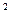 . (1.51)
. (1.51)
Равенство (1.51) означает, что приближенное решение является наилучшей в смысле энергетической нормы аппроксимацией точного решения функциями из 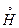 , т.е. кусочно-линейными функциями. Тем самым оценка погрешности в МКЭ, так же как в других проекционных методах, сводится к классической задаче аппроксимации функций. Следствием (1.51) является неравенство
, т.е. кусочно-линейными функциями. Тем самым оценка погрешности в МКЭ, так же как в других проекционных методах, сводится к классической задаче аппроксимации функций. Следствием (1.51) является неравенство
|| 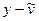 ||
|| 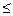 ||
|| 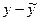 ||, (1.52)
||, (1.52)
где 
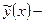 кусочно-линейная функция из
кусочно-линейная функция из 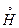 , построенная по значениям
, построенная по значениям 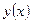 в узлах сетки, т.е. кусочно-линейная интерполяция
в узлах сетки, т.е. кусочно-линейная интерполяция 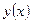 . Таким образом, вопросы сходимости метода и оценка скорости сходимости сведены к выяснению поведения величины ||
. Таким образом, вопросы сходимости метода и оценка скорости сходимости сведены к выяснению поведения величины || 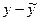 ||.
||.
Оценки аппроксимации
Оценим величину || 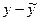 || в предположении, что
|| в предположении, что 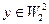 . Прежде всего
. Прежде всего
|| 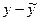 ||
|| 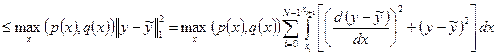 .
.
Проведем оценки на 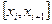 . Имеем
. Имеем
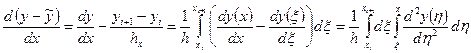 .
.
Возведем равенство в квадрат и проинтегрируем по промежутку  . Получим
. Получим
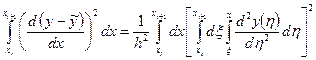 .
.
Оценим выражение в квадратных скобках, расширив промежуток интегрирования:
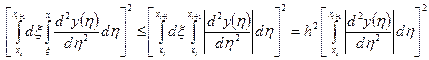 .
.
Применяя к последнему интегралу неравенство Кони – Буняковского, получим
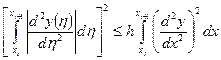 .
.
В итоге на каждом интервале 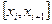 имеем
имеем
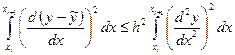 . (1.53)
. (1.53)
Суммируя эти оценки, получим неравенство
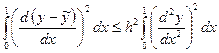 .
.
Оценим теперь 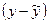 . На каждом интервале справедливо представление
. На каждом интервале справедливо представление
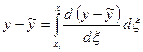 ,
,
так как 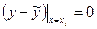 . Используя это представление, а также оценку (1.53), получим сначала для промежутка
. Используя это представление, а также оценку (1.53), получим сначала для промежутка 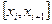 , а затем для всего интервала
, а затем для всего интервала 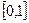 оценку
оценку
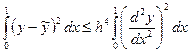 .
.
Таким образом, доказаны аппроксимационные неравенства
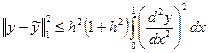 , (1.54)
, (1.54)
|| 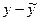 ||
|| 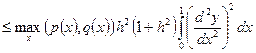 .
.
Из (1.52) и (1.54) следует, что
|| 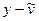 ||
|| 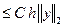 . (1.55)
. (1.55)
Таким образом, показано, что МКЭ сходится со скоростью 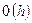 в энергетической норме. В силу эквивалентности
в энергетической норме. В силу эквивалентности 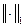 и ||
и ||  || имеет место сходимость и в норме пространства
|| имеет место сходимость и в норме пространства 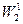 .
.
