Расчет числителей простых дробей
Метод неопределенных коэффициентов (системы уравнений). Универсальный, хотя и громоздкий, метод, пригодный для любых корней характеристического полинома.
Левую и правую часть разложения на простые дроби приводят к общему знаменателю, который отбрасывается. Приравнивая коэффициенты при одинаковых степенях s левой и правой частей равенства, составляют систему линейных алгебраических уравнений и решают ее любым известным методом.
Пример. Изображение 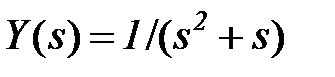 разлагается на две дроби
разлагается на две дроби
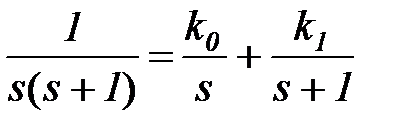
в соответствии с полюсами s1 = 0; s2 = -1. Приводим левую и правую части к общему знаменателю, отбрасывая его, группируем коэффициенты, приравниваем коэффициенты при одинаковых степенях s слева и справа
1=k0s +k0 + k1s = (k0 + k1)s + k0
| при s0 → при s1 → | 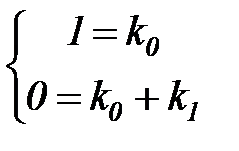 | откуда | k0 = 1 k1 = -1 |
Подставляем значения коэффициентов числителей
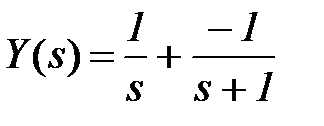
и переходим по таблице соответствия от изображений к оригиналам
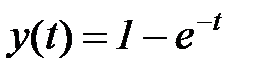 .
.
Метод подстановки полюсов (пригоден только для простых полюсов или дроби с полюсом максимальной кратности).
Формула: 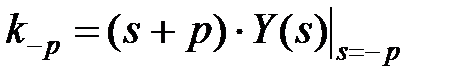
Пример: возьмем ту же функцию 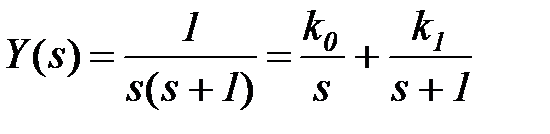 .
.
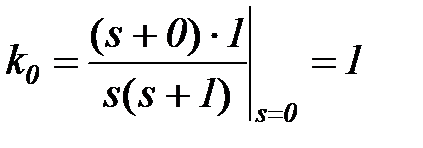 ;
; 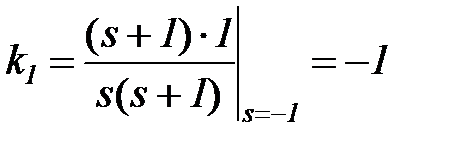 ,
,
получили аналогичный результат. Действия сводятся к тому, что в знаменателе левой части равенства исключают полином с соответствующим полюсом, а в оставшуюся часть подставляют его значение.
Метод вычисления производной (для простых полюсов).
Формула: 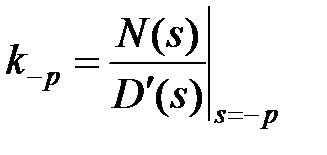 .
.
Пример: возьмем ту же функцию 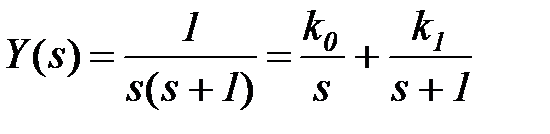 .
.
От знаменателя изображения D(s) = s2 + s вычисляем производную 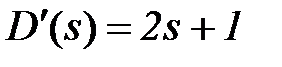 и находим коэффициенты
и находим коэффициенты
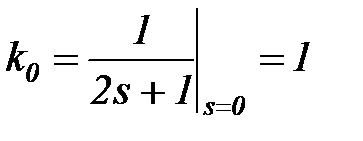 ;
; 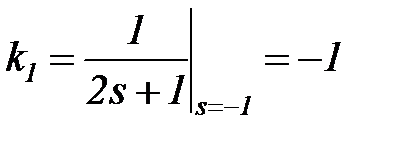 .
.
Метод вычисления производной (для кратных полюсов). Исходное изображение необходимо разделить на две части – часть, содержащую кратные корни, и оставшуюся часть F(s). Кратные корни в правой части выражения записывают по убыванию кратности (степени s). Пусть разложение функции имеет вид, где 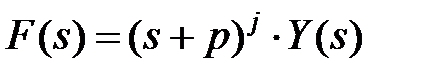
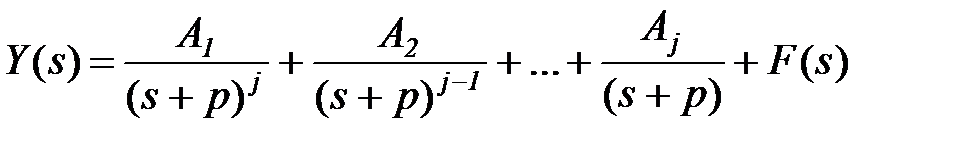 ,
,
тогда формула для вычисления коэффициента числителя Ar (1< r ≤ j) дроби с кратным корнем
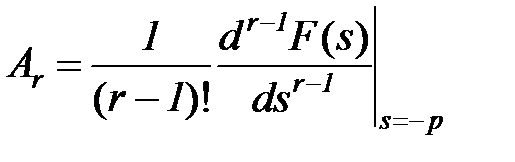 .
.
Пример: дана функция с простым корнем s = -1 и корнем s = 0 с кратностью 3
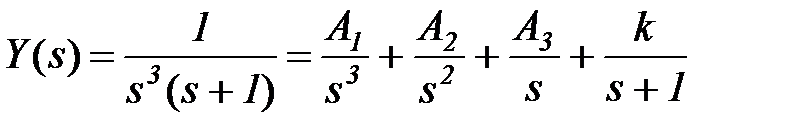 .
.
Остаток после удаления кратных корней равен F(s) = 1/(s+1) = (s+1)-1. Коэффициенты А1 и k определяем другим способом, например, подстановкой полюсов
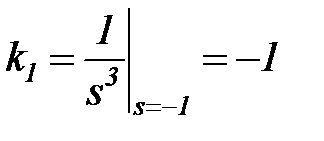 ;
; 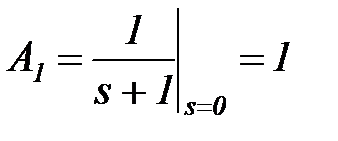 .
.
Остальные коэффициенты
r = 2 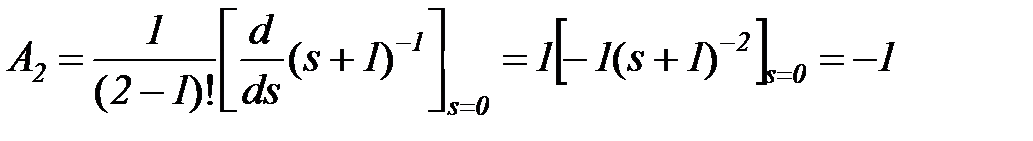 ,
,
r = 3 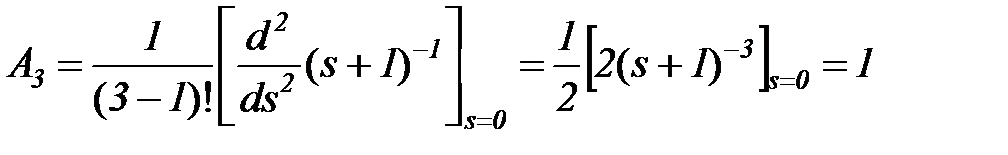
и реакция в целом
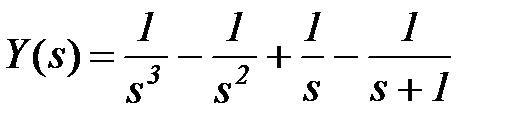 (изображение),
(изображение),
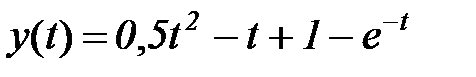 (оригинал).
(оригинал).
Метод вычитания найденной дроби (для кратных полюсов). Пример: дана функция с простым корнем s = -1 и корнем s = 0 с кратностью 3
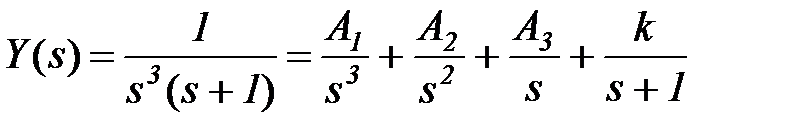 .
.
Находим сразу А1 = 1 любым методом, например, подстановкой полюсов. Вычитаем найденную дробь из левой части
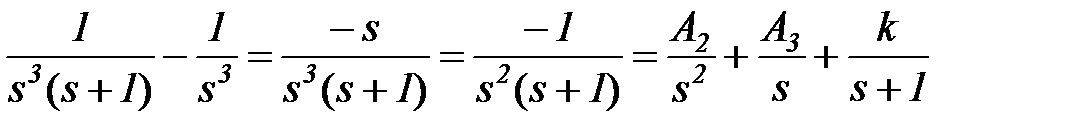
и определяем А2 каким-либо методом, например, подстановкой полюсов
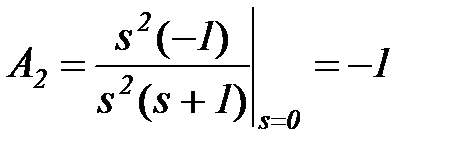 .
.
Снова вычитаем найденную дробь
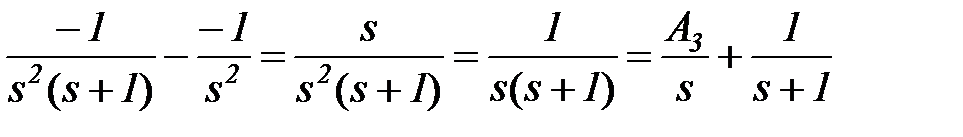 .
.
Осталось найти методом подстановки полюсов А3 = 1 и k = -1, т.е. получены те же результаты, что и в предыдущем примере.
Контрольные вопросы и задачи
1. Сравните характеристики дифференцирующего и реально дифференцирующего звеньев. Что в них общего, и чем они отличаются?
2. Сравните характеристики интегрирующего звена и интегрирующего звена с запаздыванием. Что в них общего, и чем они отличаются?
Практическая работа № 4
«Основные правила составления и преобразования структурных схем и определение передаточных функций систем»
Цель работы:
Ознакомление с правилами эквивалентных преобразований структурных схем систем автоматического управления и представлении математической модели САУ с помощью ориентированных графов (орграфов).
Общие сведения
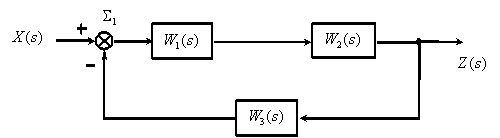
САУ представляет собой систему, состоящую из функциональных элементов, каждый из которых может быть представлен в виде динамического звена. То есть САУ можно представить в виде совокупности динамических звеньев с известными математическими моделями. Рассмотрим структуру типичной САУ представленной на рисунке 4.1.
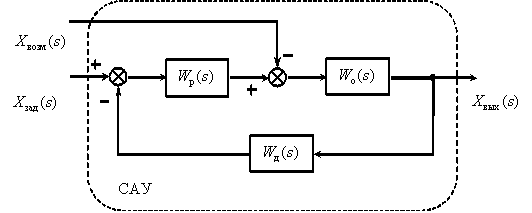
Рисунок 4.1 Структурная схема системы автоматического управления
где 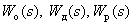 – передаточные функции соответственно объекта, датчика и регулятора,
– передаточные функции соответственно объекта, датчика и регулятора, 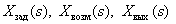 – изображения задающего, возмущающего и выходного сигналов.
– изображения задающего, возмущающего и выходного сигналов.
В процессе анализа и синтеза САУ необходимо получать передаточные функции САУ, которые связывают выходную переменную с заданием и возмущением в САУ, по известным структурной схеме и передаточным функциям динамических звеньев, входящих в состав САУ.
Аналогичная задача возникает в том случае, когда известны частотные характеристики динамических звеньев, а необходимо определить частотные характеристики САУ, характеризующие связи между выходом и входом САУ.
Эта задача решается путем преобразования (сворачивания) структурной схемы к одному динамическому звену с искомой передаточной функцией на основе использования правил эквивалентных преобразований структурных схем и принципа суперпозиции (наложения).
Правила эквивалентных преобразований позволяют найти необходимую передаточную функцию САУ, свернув структурную схему к одному динамическому звену с искомой передаточной функцией.
Рассмотрим правила эквивалентных преобразований, не изменяющих свойств систем и необходимых для нахождения передаточной функции:
1. Последовательное соединение динамических звеньев.
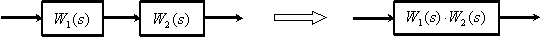
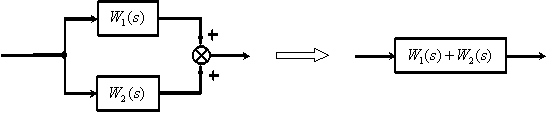
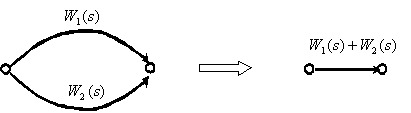
2. Параллельное соединение динамических звеньев.
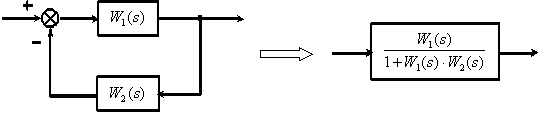
3. Замкнутый контур с отрицательной обратной связью.
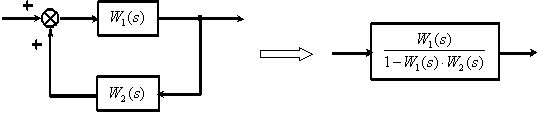
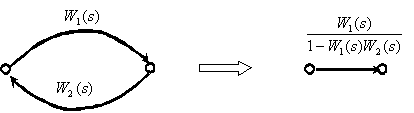
4. Замкнутый контур с положительной обратной связью.
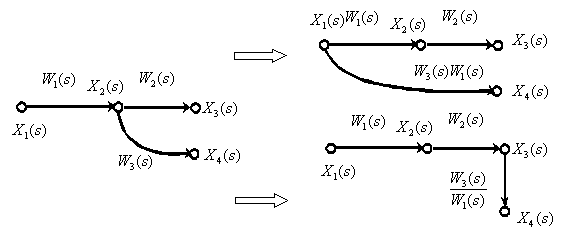
5. Перенос точки ветвления через динамическое звено.
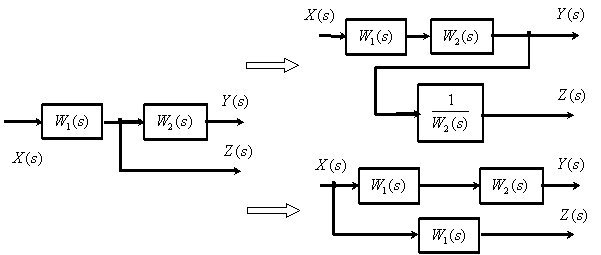
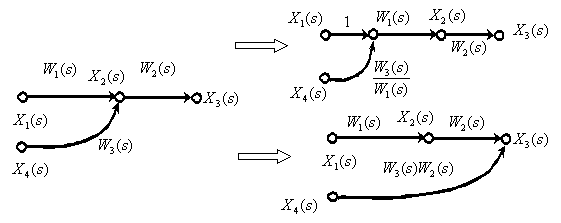
6. Перенос суммирующего звена через динамическое звено.
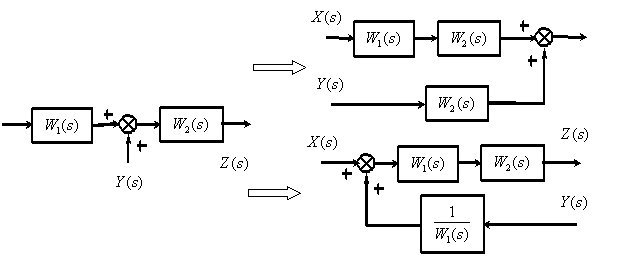
7. Перестановка суммирующих звеньев.
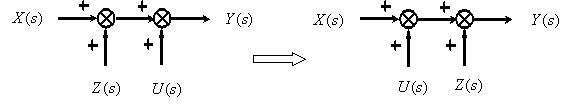
8. Перенос точки ветвления с выхода на вход суммирующего звена.
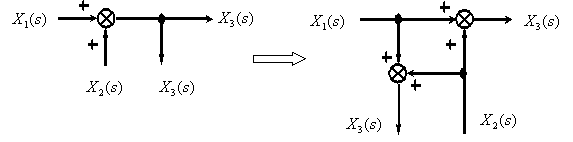
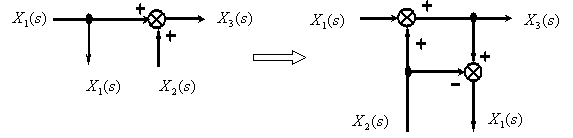
9. Перенос точки ветвления с входа на выход суммирующего звена.
Математическую модель САУ можно наглядно представить с помощью ориентированных графов (орграфов).
Орграфы используются в сложных САУ, особенно при управлении и автоматизации технологических процессов в промышленности, когда описание в виде структурных схем становится громоздким и сложным для восприятия. Рассмотрим простейший орграф динамического звена САУ рисунок 4.2
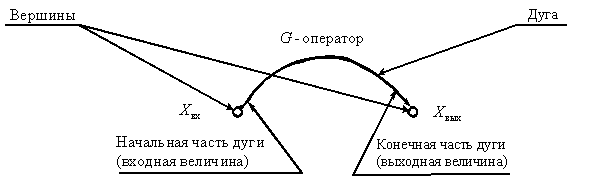
Рисунок 4.2
Орграфом САУ является графическое представление САУ в виде совокупности вершин, соответствующих переменным, и дуг, соединяющих вершины.
Рассмотрим основные свойства орграфа:
1. Каждая дуга со стрелкой, указывающей направление распространения сигнала, изображает звено и характеризуется оператором изображаемого звена (передаточной функцией);
2. Каждой вершине, отмеченной кружком, ставится в соответствие одна из переменных САУ (изображение переменной по Лапласу);
3. Входная величина дуги равна переменной вершины, из которой эта дуга исходит;
4. Выходная величина дуги получается как результат преобразования оператором входной величины;
5. Если к вершине подходят несколько дуг, то соответствующая вершине переменная равна сумме выходных величин этих дуг (аналог суммирующего звена структурных схем);
6. Если из вершины исходит несколько дуг, то входные величины всех этих дуг одинаковы (аналог точки ветвления в структурных схемах).
Ориентированный граф (орграф) можно построить по структурной схеме и наоборот. При построении орграфа по структурной схеме необходимо придерживаться следующих правил:
1. Модифицируют структурную схему так, чтобы в сумматорах все переменные складывались с положительным знаком, отрицательные знаки вносятся в передаточные функции соответствующих звеньев;
2. Каждый сумматор структурной схемы заменяется вершиной, которой ставится в соответствие выходная переменная сумматора;
3. Каждое динамическое звено заменяется дугой с оператором, равным передаточной функции звена;
4. Каждой переменной, включая и входные воздействия, соответствует своя вершина.
Указания по выполнению работы:
1)Определить замкнутую и разомкнутую передаточные функции относительно выходного воздействия – у по входному воздействию – х для системы автоматического управления со следующей структурной схемой
Решение
Предварительно заполните таблицу, подобрав к каждому алгоритму конкретное соответствие из данного задания.
| № п/п | Алгоритм | Краткое соответствие данной ситуации предложенному алгоритму |
| Определить позиционное расположение сумматоров и узлов и тип соединения элементарных звеньев в схеме. | Структурная схема состоит из пяти элементарных звеньев, в ней два узла и два сумматора. Тип соединения звеньев – последовательное, параллельное и с отрицательной обратной связью. | |
| Определить элементарные звенья, входящие в прямую цепь и в цепь обратной связи и пользуясь правилами записи передаточной функции для нескольких звеньев , записать общую передаточную функцию прямой цепи и обратной связи | В прямую цепь входят звенья 1,2,3,4, в цепь обратной связи входит звено 5. Передаточная функция прямой цепи Передаточная функция цепи обратной связи | |
| Осуществить условный разрыв главной обратной связи перед сумматором и, пользуясь правилами записи передаточной функции для нескольких звеньев , записать общую передаточную функцию разомкнутой цепи. | Условно разрываемая цепь обратной связи перед сумматором ( в точке А). Передаточная функция разомкнутой цепи определяется как произведение ранее полученных передаточных функций: | |
| Пользуясь правилами записи передаточной функции для группы звеньев ,соединенных по схеме с обратной связью , записать общую передаточную функцию замкнутой цепи. | Передаточная функция замкнутой цепи ( или собственно системы автоматического управления) определяется следующим образом: |
2) Найти передаточные функции замкнутой системы автоматического управления относительно выходного воздействия по входному и возмущающему воздействиям для следующей структурной схемы (x – входное, y – выходное, f – возмущающее воздействия):
Решение
Предварительно заполните таблицу, подобрав к каждому алгоритму конкретное соответствие из данного задания.
Решение
Предварительно заполните таблицу, подобрав к каждому алгоритму конкретное соответствие из данного задания.
| № п/п | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| Произвести анализ структурной схемы САУ и определить пути необходимых преобразований. | В структурной схеме САУ 4 сумматора (1,2,3,4) и 3 узла (а,б,в). Необходимо избавиться от перекрестных связей и выделить отдельную цепь для возмущающего воздействия. | |
| Осуществить преобразование структурной схемы в соответствии с принципом суперпозиции и правилами переноса узла и сумматора. | Перенесем узел «а» через звено W3 по направлению действия сигнала и с учетом принципа суперпозиции выделим отдельную цепь для возмущающего воздействия. Получится следующая структурная схема: |
| № п/п | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| Записать передаточную функцию САУ по преобразованной структурной схеме. | Применяя умение №1, определяем передаточную функцию по входному сигналу: 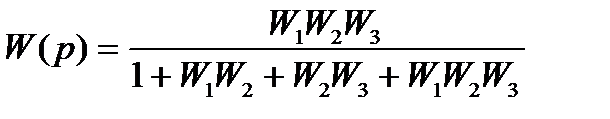 и передаточную функцию по возмущению: и передаточную функцию по возмущению: 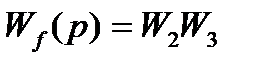 |
Как правило, по структурной схеме при известных функциях передачи отдельных звеньев требуется найти эквивалентную передаточную функцию (ПФ) некоторого объединения звеньев (объекта, регулятора), либо всей системы в целом. Для этого используют правила преобразования последовательного, параллельного и встречно-параллельного (с обратной связью) соединений.
Эквивалентная передаточная функция последовательно соединенных звеньев равна произведению передаточных функций этих звеньев. Считают, что перестановка последовательно включенных по пути сигнала звеньев не влияет на результат, т. е. W1W2 = W2W1.
Эквивалентная передаточная функция параллельно соединенных звеньев равна сумме передаточных функций этих звеньев (с учетом знака входа сумматора на пути сигнала).
Путь от входа к выходу системы называется прямой связью, от выхода ко входу – обратной связью. Если сигнал на пути меняет знак (обычно на инвертирующем входе сумматора), обратная связь называется отрицательной (ООС), если не меняет знак – положительной (ПОС). Замкнутый путь называется контуром, например, замкнутый контур обратной связи (ЗКОС). Эквивалентная передаточная функция соединения с обратной связью равна дроби, в числителе которой записана ПФ звена на прямом пути, а в знаменателе – единица минус произведение ПФ звеньев по замкнутому контуру обратной связи. Величина 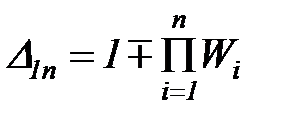 называется определителем ЗКОС.
называется определителем ЗКОС.
Особенности этого вида соединения звеньев:
- если в системе есть хоть одна обратная связь, передаточная функция системы будет всегда представлять собой дробь;
- знак перед произведением ПФ звеньев в знаменателе (в определителе ЗКОС) обычно противоположен знаку обратной связи.
Для систем с перекрещивающимися (мостиковыми) связями применяют правило переноса: в переносимую ветвь вводят фиктивное звено с передаточной функцией, равной ПФ потерянного, либо обратной ПФ появившегося при переносе элемента.
По Мейсону структурная схема может быть описана целиком, без деления на звенья. Передаточная функция многоконтурной системы образует дробь, числитель которой равен сумме произведений передаточных функций прямых путей на совокупные определители ЗКОС, не касающихся этих путей, а знаменатель – единица минус сумма произведений определителей несоприкасающихся ЗКОС и передаточных функций общих ЗКОС. Следует внимательно относиться к ветвям, которые заходят извне в контур ОС, т.к. они могут образовывать неявные прямые пути по цепям обратных связей.
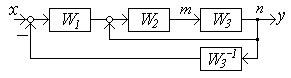
Пример 1. Определить передаточную функцию схемы (рисунок 4.3, а).
 |  |
а б
Рисунок 4.3
Видно, что без преобразований нельзя начинать сворачивать схему, в частности, нельзя объединить звенья W2 и W3, как последовательно включенные, из-за связи в точке m. Перенесем ветвь из узла m в узел n (рисунок 4.3, б).
В исходной схеме на пути от точки m к входному сумматору не было звеньев, преобразующих сигнал, а в новой схеме на пути между теми же точками появляется звено с передаточной функцией W3. Следовательно, в цепь переносимого воздействия нужно ввести фиктивное звено с обратной передаточной функцией, т. е. 1/W3 или W3-1.
После переноса начнем свертывание схемы, заменяя каждый раз несколько звеньев одним эквивалентным на основе правил 1-3 и увеличивая границы преобразуемого участка. Промежуточные (вспомогательные) ПФ обычно индексируют римскими цифрами, их используют временно и обязательно заменяют в итоге на ПФ с реально существующими индексами.
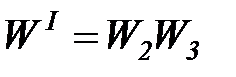 ;
; 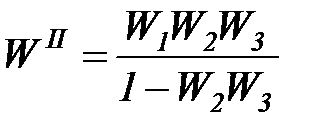 ;
;
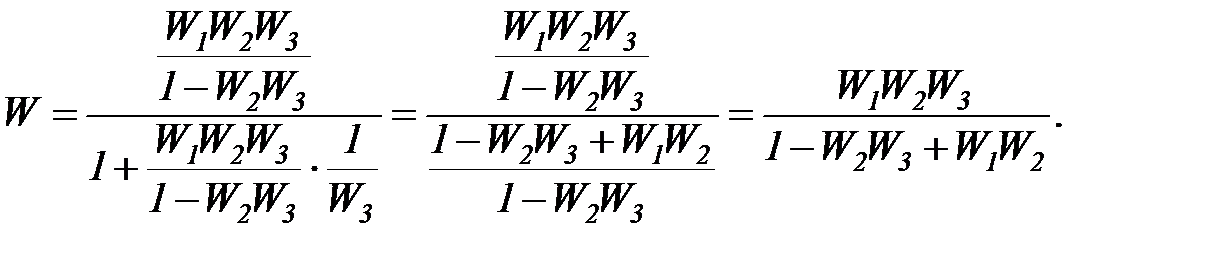
Конечный результат всегда представляется в виде простой рациональной дроби и выражается только через исходные передаточные функции. Сигнал не может пройти через одну и ту же точку дважды, поэтому появление в выражении кратных величин вида 2Wi или Wi2 и т. п. является признаком допущенной при преобразованиях ошибки.
Пример 2. Определить передаточную функцию схемы (рисунок 4.4).
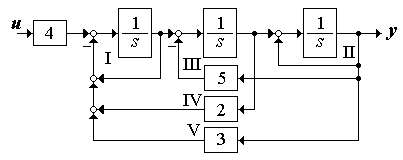
Рисунок 4.4
Применим правило Мейсона. В системе имеются обратные связи, поэтому ПФ представляет собой дробь. Прямой путь от входа u к выходу y только один, его касаются все пять ЗКОС, поэтому в числителе ПФ пишем просто произведение 4/s3. Знаменатель начинаем описывать с несоприкасающихся контуров – контур I не имеет общих точек с контуром III и вложенным в него контуром II, поэтому записываем сначала произведение их определителей. Контур IV соприкасается с контурами I и III, поэтому просто добавляем произведение звеньев по нему 2/s2, но умножаем его на определитель контура II, так как этот ЗКОС не имеет общих точек с IV. И в конце просто добавляем произведение звеньев 3/s3 контура V, поскольку он соприкасается со всеми остальными ЗКОС
Пример 3. Рассмотрим сначала многоконтурную САР без перекрещивающихся связей (рис. 4.5). Передаточные функции всех звеньев  системы известны. Надо найти передаточную функцию разомкнутой Wраз(р) и замкнутой
системы известны. Надо найти передаточную функцию разомкнутой Wраз(р) и замкнутой  систем.
систем.
Рис. 4.5. Структурная схема многоструктурной замкнутой САР без перекрещивающихся связей.
Решение.
Применяя правила структурных преобразований, преобразуем структурную схему рис. 4.5 к более простой эквивалентной одноконтурной замкнутой структурной схеме рис. 4.6.
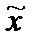 |
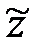 |
| W*(p) |
W 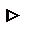 (p) (p) |
| W9(p) |
| Рис. 4.6. Одноконтурная замкнутая структурная схема САР. |
 |
На этом рисунке звено W*(p) заменяет три параллельно соединенных звена, поэтому
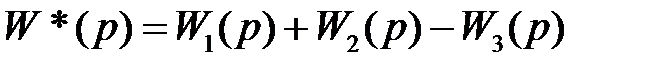 .
.
Звено W 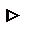 (p) есть эквивалент звена W4(p), охваченного положительной обратной связью W5(p), следовательно
(p) есть эквивалент звена W4(p), охваченного положительной обратной связью W5(p), следовательно
W 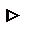 (p)
(p) 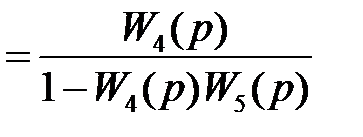 .
.
Звено 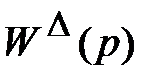 представляет собой звено W6(р), охваченное в обратной связи параллельным соединением звеньев W7(p) и W8(p), значит
представляет собой звено W6(р), охваченное в обратной связи параллельным соединением звеньев W7(p) и W8(p), значит
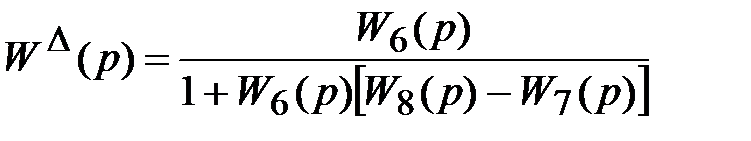
 .
.
Теперь, опираясь на рис.4.6, найдем
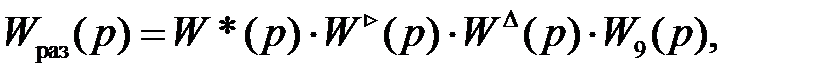
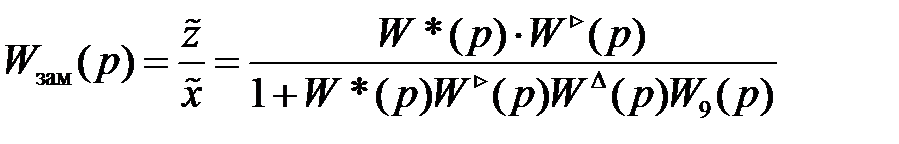 .
.
Подставив сюда найденные значения W*(p), W 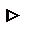 (p) и
(p) и 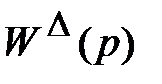 , получим Wраз(р) и Wзамз(р) через заданные передаточные функции звеньев
, получим Wраз(р) и Wзамз(р) через заданные передаточные функции звеньев 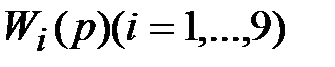 .
.
Пример 4. Дана структурная схема многоконтурной САР с перекрещивающимися связями. Передаточные функции 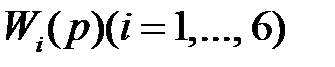 звеньев, входящих в САР, заданы. Требуется найти передаточные функции разомкнутой Wраз(р) и замкнутой
звеньев, входящих в САР, заданы. Требуется найти передаточные функции разомкнутой Wраз(р) и замкнутой 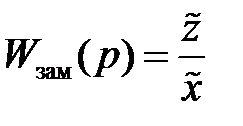 систем.
систем.
Рис. 4.7. Структурная схема многоконтурной замкнутой САР с перекрещивающими связями.
Решение.
Попытаемся освободиться от перекрещивающихся связей. Для этого узел А против хода сигнала перенесем через звено W2(р) в т. Б, узел В тоже против хода перенесём через звенo W5(р) в т. Г. Одновременно для удобства сумматор 1 разобьем на два сумматора 1 и 2. В результате получим следующую структурную схему
Рис. 4.8. Результат первого преобразования
структурной схемы многоконтурной САР.
После первого преобразования САР осталась многоконтурной с перекрещивающимися связями (звено W3(р) принадлежит двум контурам одновременно). От перекрестных связей можно было бы освободиться и в процессе первого преобразования, но пришлось бы ряд операций проводить в уме, что повышает вероятность ошибки.
Чтобы освободиться от оставшейся перекрестной связи, перенесем сумматор 3 против хода сигнала через звено W3(р) и, поменяв его затем местами с сумматором 2, объединим сумматоры 1 и 3 в один. В результате получим структурную схему, изображённую на рис. 4.9.
Теперь используя правила структурных преобразований, преобразуем эту многоконтурную САР без перекрестных связей в одноконтурную замкнутую САР (рис.4.10).
Рис. 4.9. Результат второго преобразования
структурной схемы многоконтурной САР.
Отсюда можно найти
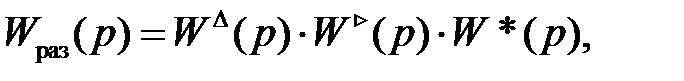
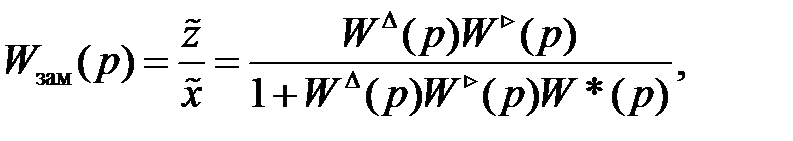
имея в виду, что
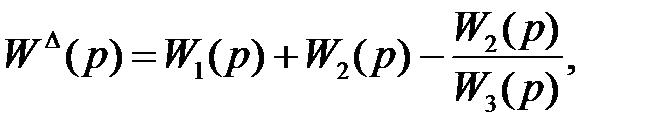
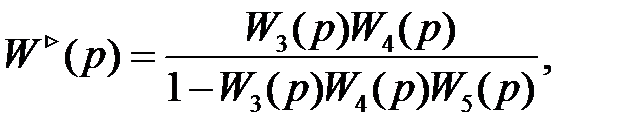
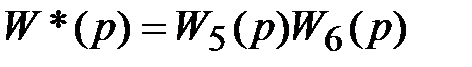 .
.
Пример 5. Пусть задана следующая структурная схема системы (рис. 4.11.):
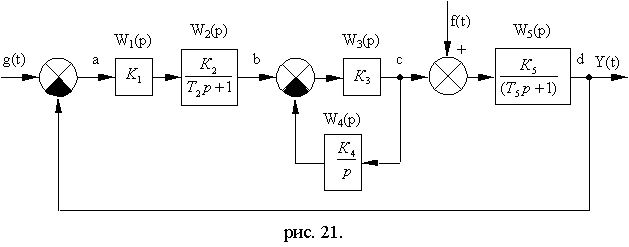
Рис. 4.11
1.Используя правила преобразования структурных схем, определим эквивалентную передаточную функцию между точками “b” и “c”:
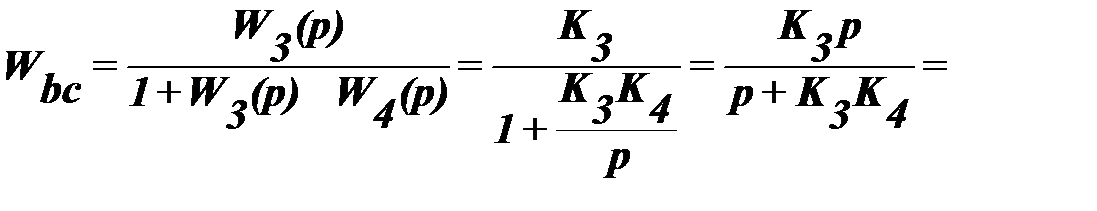
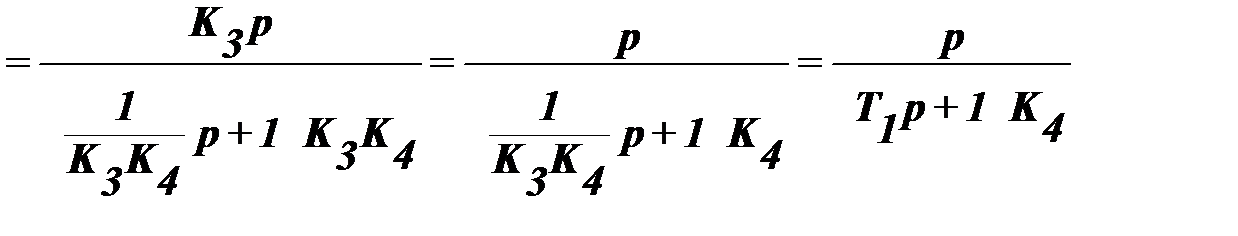 , где T1=
, где T1= 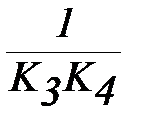 .
.
2. Передаточная функция системы разомкнутой на главной обратной связи
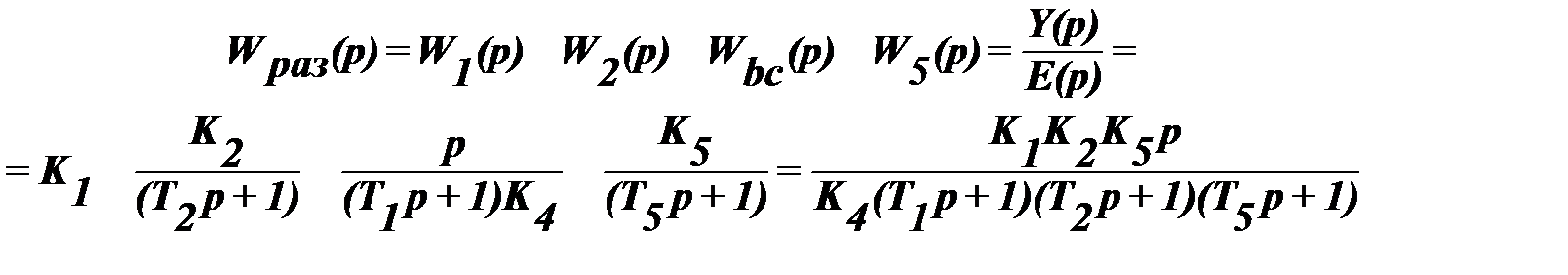
3. Эквивалентная функция системы в замкнутом состоянии.
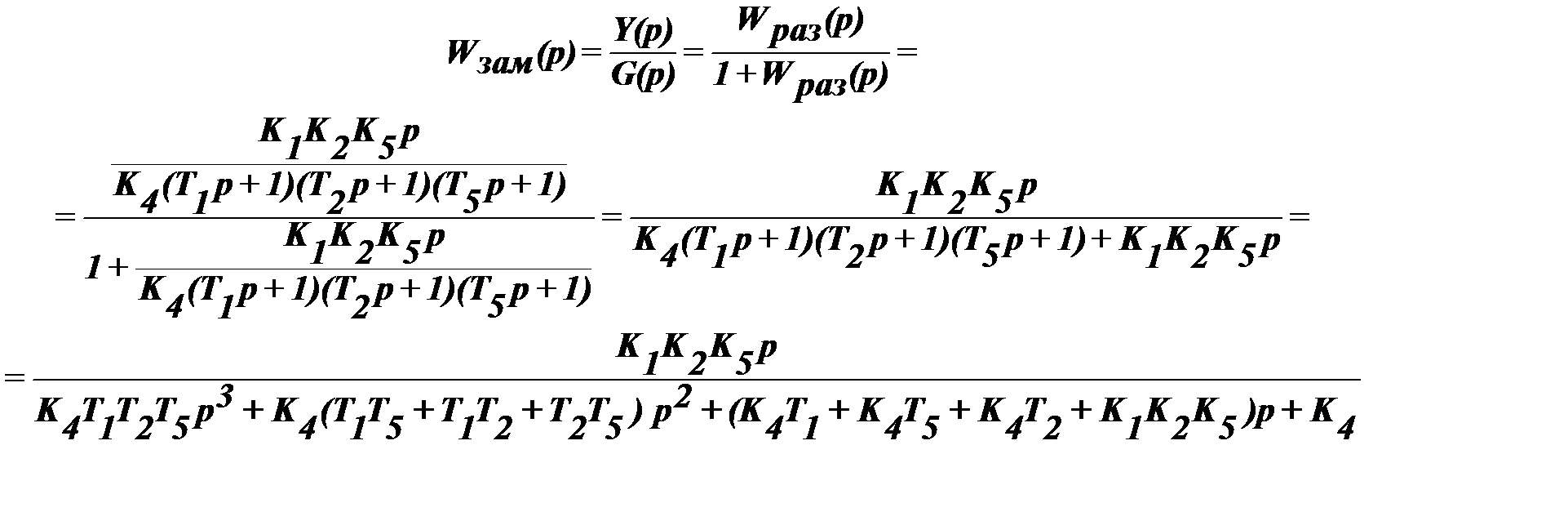
4. Передаточная функция ошибки относительно задающего воздействия:
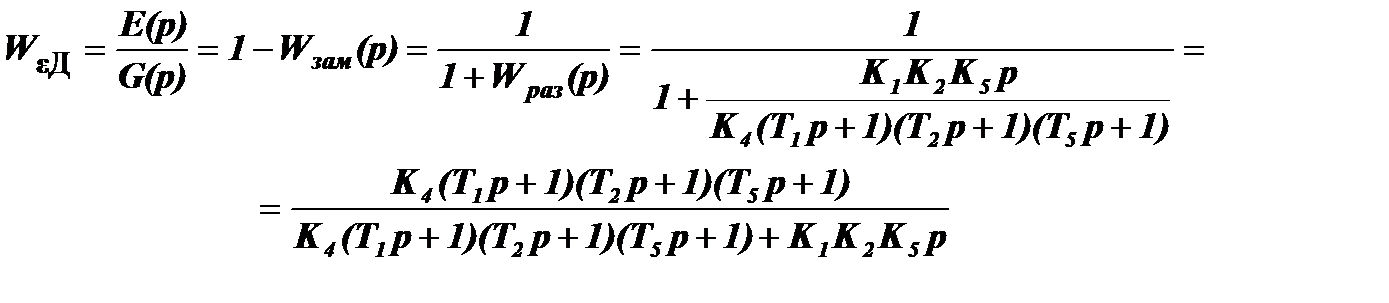
5. Передаточная функция системы относительно возмущения f(t) (точка приложения возмущения – вход)
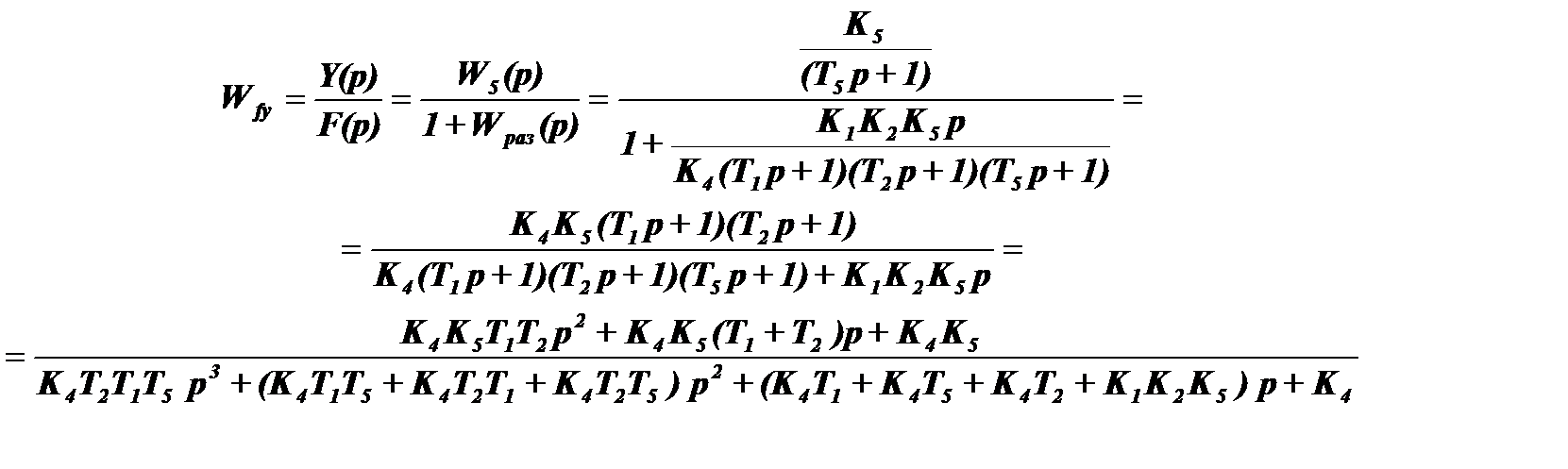
6. Изображение выходного сигнала: Y(p) = G(p) Wзам (p) + F(p) Wfy (p).
7. Уравнение системы в изображениях
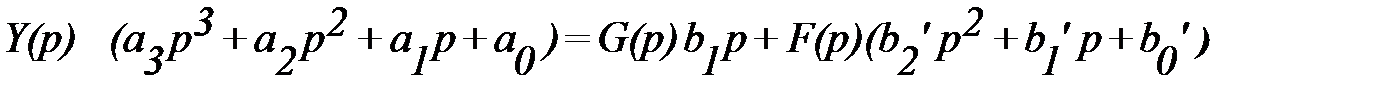 ,
,
где 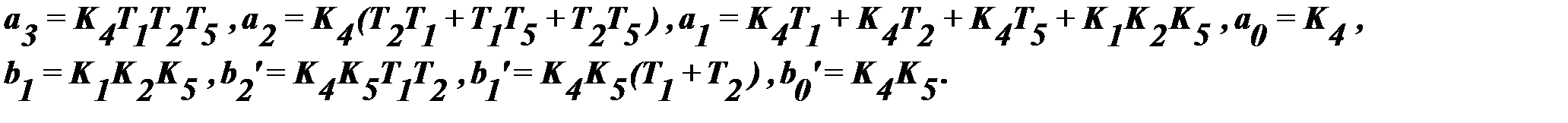
8. Уравнение движения системы в дифференциальной форме
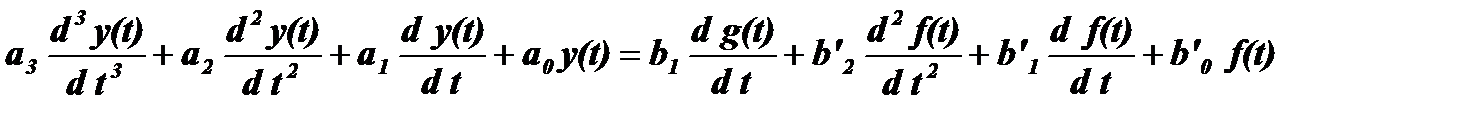 .
.
Принцип суперпозиции (наложения)
Применим рассмотренные правила для упрощения структурной схемы представленной на рисунке 4.12
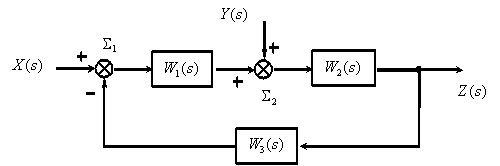
Рисунок 4.12
Процесс преобразования, который часто называют свертыванием структурной схемы, выглядит следующим образом.
1. Перенесем суммирующее звено  через динамическое звено
через динамическое звено  .
.
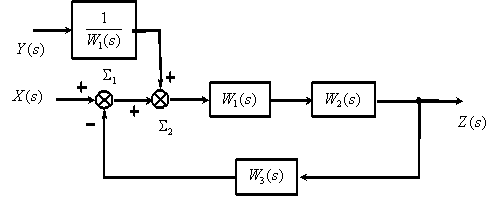
2. Поменяем местами суммирующие звенья  и
и  .
.
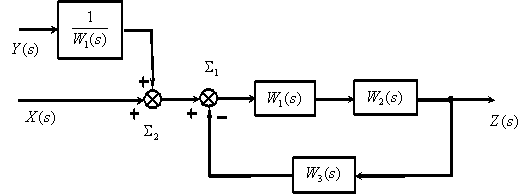
3. Преобразуем последовательно включенные динамические звенья 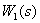 и
и 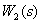 .
.
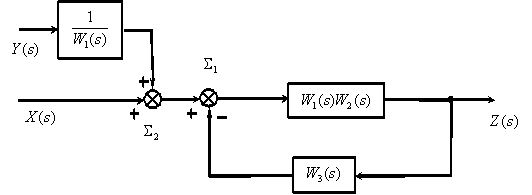
4. Преобразуем замкнутый контур с отрицательной обратной связью ( 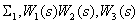 ).
).
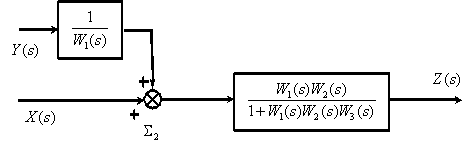
5. Перенесем суммирующее звено  вправо.
вправо.
6. Преобразуем последовательно включенные звенья..
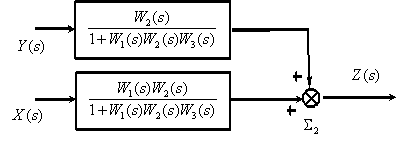
В соответствии с полученной структурной схемой запишем операторное уравнение –
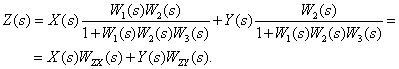 | (4.1) |
Уравнение показывает, что 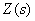 является линейной комбинацией изображений входных сигналов, взятых с коэффициентами
является линейной комбинацией изображений входных сигналов, взятых с коэффициентами 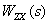 и
и 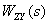 . Выясним смысл этих коэффициентов на примере коэффициента
. Выясним смысл этих коэффициентов на примере коэффициента 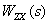 . Для этого положим в (4.1)
. Для этого положим в (4.1) 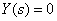 , тогда получим –
, тогда получим –
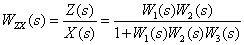 | (4.2) |
Таким образом, из (4.2) следует, 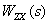 – это передаточная функция динамического звена, к которому свернута структурная схема в предположении, что изображения всех входных сигналов, кроме
– это передаточная функция динамического звена, к которому свернута структурная схема в предположении, что изображения всех входных сигналов, кроме 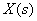 , равны нулю.
, равны нулю.
Смысл операторного уравнения (4.1), описывающего систему заключается в том, что реакция линейной системы на совместно действующие входные сигналы может быть определена в виде суммы частичных реакций, каждая из которых вычисляется в предположении, что на систему действует только один входной сигнал, а остальные равны нулю.
По сути – это формулировка фундаментального принципа, который называют принципом наложения или суперпозиции. Этот принцип можно рассматривать как дополнение к правилам эквивалентных преобразований структурных схем и активно использовать на практике.
Практически принцип суперпозиции для нахождения конкретной передаточной функции используют следующим образом. Полагают равными нулю все входные сигналы, кроме необходимого сигнала, а затем выполняют преобразование структурной схемы в одно динамическое звено.
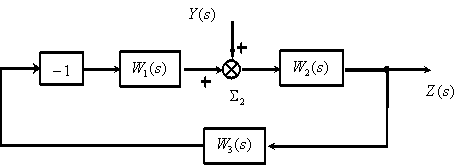
Рассмотрим использование принципа суперпозиции на примере показанной на рисунке 3 структурной схемы.
1. Полагаем  и изобразим соответствующую этому случаю структурную схему.
и изобразим соответствующую этому случаю структурную схему.
Используя эквивалентные преобразования, получим –
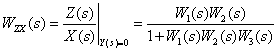 .
.
2. Полагаем 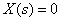 и изобразим соответствующую этому случаю структурную схему.
и изобразим соответствующую этому случаю структурную схему.
Используя эквивалентные преобразования, получим –
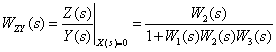 .
.
3. Имея 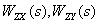 , в соответствии с принципом суперпозиции получим "свернутую" структурную схему САУ.
, в соответствии с принципом суперпозиции получим "свернутую" структурную схему САУ.
2) Ориентированные графы систем автоматического управления:
Рассмотрим пример. На рисунке 4.13 показана структурная исходная схема, на рисунке 4.14 показан полученный орграф САУ.
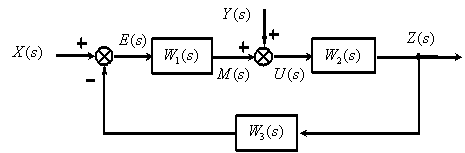
Рисунок 4.13
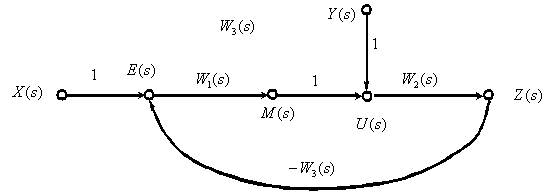
Рисунок 4.14
Преобразовать орграф САУ можно, как и структурную схему, используя правила эквивалентных преобразований для орграфов, которые легко могут быть получены по аналогичным правилам для структурных схем.
1. Последовательное соединение динамических звеньев.

2. Параллельное соединение динамических звеньев.
3. Замкнутый контур с отрицательной обратной связью.
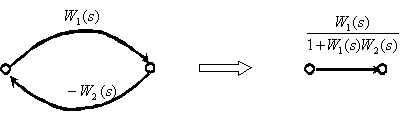
4. Замкнутый контур с положительной обратной связью.
5. Перенос точки ветвления через динамическое звено.
6. Перенос суммирующего звена через динамическое звено.
Использование формулы Мейсона для преобразования структурных схем и ориентированных графов
Когда структурная схема преобразована в орграф, для нахождения необходимой передаточной функции можно использовать формулу Мейсона (правило некасающихся контуров), которая позволяет получить передаточную функцию, связывающую переменные в сложных, многоконтурных САУ.
Рассмотрим общий вид формулы и поясним ее компоненты:
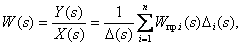 | (4.3) |
где 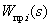 - передаточная функция
- передаточная функция 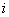 -го отдельного прямого пути от
-го отдельного прямого пути от 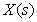 до
до 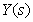 , вычисленная как произведение передаточных функций дуг, входящих в этот путь;
, вычисленная как произведение передаточных функций дуг, входящих в этот путь;
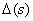 - определитель орграфа.
- определитель орграфа.
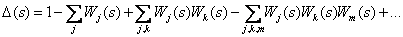 | (4.4) |
где 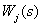 - передаточная функция
- передаточная функция 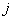 -го замкнутого контура, вычисленная как произведение передаточных функций дуг, входящих в этот контур;
-го замкнутого контура, вычисленная как произведение передаточных функций дуг, входящих в этот контур;
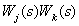 - произведение передаточных функций пары (
- произведение передаточных функций пары ( 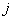 -го и
-го и 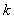 -го) замкнутых контуров, не касающихся ни дугами, ни вершинами, суммирование осуществляется по всем парам некасающихся контуров;
-го) замкнутых контуров, не касающихся ни дугами, ни вершинами, суммирование осуществляется по всем парам некасающихся контуров;
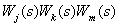 - произведение тройки (
- произведение тройки ( 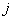 -го,
-го, 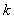 -го и
-го и 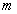 -го) некасающихся контуров, суммирование производится по всем тройкам не касающихся контуров.
-го) некасающихся контуров, суммирование производится по всем тройкам не касающихся контуров.
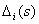 - определитель орграфа, полученного при удалении дуг и вершин
- определитель орграфа, полученного при удалении дуг и вершин 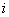 -го отдельного прямого пути, определяется по формуле (4.4).
-го отдельного прямого пути, определяется по формуле (4.4).
Поясним использование формулы Мейсона.
В начале выявляются все отдельные прямые пути между входной и выходной переменными, для которых необходимо определить передаточную функцию. Отдельным прямым путем считается такая последовательность дуг и вершин, которая соединяет вершины, соответствующие входному и выходному сигналам. При этом отдельный прямой путь не должен пересекать в вершинах сам себя.
Далее выявляются все замкнутые контуры в орграфе САУ. Замкнутым считается такой контур, когда между двумя вершинами имеется как прямая, так и обратная связь. Передаточная функция замкнутого контура определяется как произведение передаточных функций всех дуг, входящих в контур с учетом знаков.
После того как выявлены все замкнутые контуры орграфа, необходимо проанализировать – есть ли контуры, которые не касаются ни дугами, ни вершинами, есть ли пары, тройки и т. д. таких контуров.
На основании полученного формируется определитель орграфа по формуле (4.2).
