НЕ НАДО) Как следует из примера удобно

НЕ НАДО) ЭВМ работает с двоичными

ЭВМ работает с двоичными числами, человеку проще воспринимать числа в десятичной системе счисления, а шестнадцатеричная форма записи наиболее компактна. Поэтому повсеместно требуется переводить числа из одной системы счисления в другую. Здесь необходимо отметить, что перевод некоторого числа из системы с основанием N₁ в систему с основанием N₂ производится одинаково для всех систем счисления, однако правила перевода целых и дробных чисел различаются. Есть некоторые нюансы при переводе дробного числа. Дело в том, что в результате перевода число может оказаться иррациональным с бесконечным числом разрядов в дробной части. Во всех ЭВМ существует ограничение на количество разрядов, с которыми она работает. Поэтому какое-то количество разрядов просто отбрасывают, т.е. производят округление числа. Естественно, в этом случае появляется разница между переводимым числом (C) и результатом его перевода (R), которая называется ошибкой округления. Рассчитать относительную ошибку перевода (ζ_%) можно по следующей простой формуле:

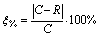(2.3)

Для того чтобы перевести целое число С_N1 в систему счисления с основанием N₂ необходимо последовательно делить его на N₂, выписывая остатки от деления, до тех пор, пока остаток от деления станет не больше N₂. Приведем пример.

Пример 2.3. Перевод числа С₁₀=41 в двоичную, восьмеричную и шестнадцатеричную системы счисления.

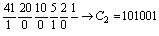
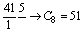
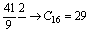
назад далее

НЕ НАДО) Как следует из примера удобно

Как следует из примера 2.3 удобно представлять процесс деления в виде последовательности цифр, разделенных чертой. Рассмотрим подробно перевод числа 41 в двоичную систему счисления. На первом шаге 41 делится на 2, частное от деления равное 20 записывается над чертой справа от делимого, а остаток от деления равный 1 под делимым. На втором шаге 20 делится на 2, частное от деления равное10 записывается над чертой справа от делимого, а остаток от деления равный 0 под делимым. Так продолжается до тех пор, пока полученное на очередном шаге делимое не станет ≤1. И, наконец, полученные остатки от деления и последнее частное записываются в порядке обратном направлению деления.

Для того чтобы перевести дробное число С_N1 в систему счисления с основанием N₂ необходимо последовательно умножать его на N₂, выписывая целые части, полученные в результате умножения, до тех пор, пока количество разрядов полученного числа не достигнет заданного. Приведем пример.

Пример 2.4. Перевод числа С₁₀=0,375 в двоичную, восьмеричную и шестнадцатеричную системы счисления

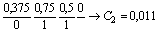
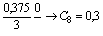
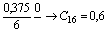
Перевод дробного числа, также удобно представлять в виде последовательности цифр, разделенных чертой. Рассмотрим подробно перевод числа 0,375 в двоичную систему счисления. На первом шаге0,375 умножается на 2, полученное множимое равное 0,75 записывается над чертой справа от 0,375, а целая часть равная 0 под множимым0,375. На втором шаге 0,75 умножается на 2, полученное множимое равное 0,5 записывается над чертой справа от 0,75, а целая часть равная 1 под множимым 0,75. Так продолжается до тех пор, пока полученное на очередном шаге множимое не станет равно 0, или не заполняться все разряды, отведенные для этого числа. И, наконец, полученные целые части записываются в прямом порядке.

3. ЛЕРА! Пример Обратный перевод чисел

Пример 2.5. Обратный перевод чисел из системы с основанием N₂ в систему с основанием N₁

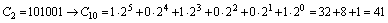
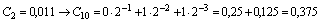
Так как двоичная, восьмеричная и шестнадцатеричная системы счисления связаны между собой через степени числа 2, то прямое и обратное преобразования между этими системами можно производить гораздо проще. Давайте, обратим внимание на таблицу 2.1.

Для перевода целого числа из двоичной системы счисления в восьмеричную (шестнадцатеричную) необходимо разбить число справа от младшего разряда на триады (тетрады), т.е. группы, состоящие из трех (четырех) цифр. Если в последней триаде (тетраде) остается менее трех (четырех) цифр, то вместо недостающих цифр слева записываются нули.

Заменив каждую триаду (тетраду) соответствующей восьмеричной (шестнадцатеричной) цифрой, получают число, записанное в восьмеричной (шестнадцатеричной) системе счисления.

Пример 2.6. Упрощенный перевод целого числа из двоичной системы счисления в восьмеричную (шестнадцатеричную)

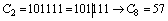
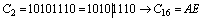
Для перевода дробного числа из двоичной системы счисления в восьмеричную (шестнадцатеричную) необходимо разбить число слева от старшего разряда на триады (тетрады). Если в последней триаде (тетраде) остается менее трех (четырех) цифр, то вместо недостающих цифр слева записываются нули. Заменив каждую триаду (тетраду) соответствующей восьмеричной (шестнадцатеричной) цифрой, получают число, записанное в восьмеричной (шестнадцатеричной) системе счисления.

Пример 2.7. Упрощенный перевод дробного числа из двоичной системы счисления в восьмеричную (шестнадцатеричную)

назад далее

Обратный перевод

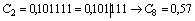
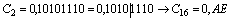
Обратный перевод осуществляется аналогично, т.е. восьмеричные (шестнадцатеричные) числа заменяются триадами (тетрадами) двоичных чисел.

назад далее

5. (Асель!) В ЭВМ используется два вида

В ЭВМ используется два вида представления чисел: с фиксированной точкой или естественная форма и с плавающей точкой илинормальная форма. Точка определяет границу раздела целой и дробной частей числа. Любая программа в ЭВМ реализуется в виде простых операций, выполняемых центральным процессором (ЦП). Одной из важнейших характеристик любого процессора является егоразрядность, т.е. количество разрядов, используемых для представления чисел. Эта величина в силу определенных причин ограничена. При использовании формы с фиксированной точкой для изображения некоторого числа, точка имеет строго определенное место для всех чисел.

Пример 2.8. Естественная форма десятичного числа

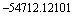
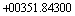
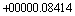
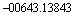
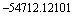
Каждое из чисел записанных в примере 2.8 имеет конечное число разрядов - 10. Пять разрядов отведены для целой части (до точки) и столько же для дробной (после точки).

Вычислительная машина, которая использовала форму представления чисел с фиксированной точкой, является «Минск-1»(точнее ее первые модели).

В ЭВМ у двоичных чисел с фиксированной точкой для точки выделяют место либо в начале (дробное число), либо в конце (целое число). Для изображения знака числа отводится специальный знаковый разряд в начале числа, в который записывает 1, если число отрицательное и 0, если число положительное.

Другой формой представления чисел в ЭВМ является нормальная форма (числа с плавающей точкой). Для организации научно-технических расчетов при моделировании, поиске экстремумов и т.п. обрабатываемые числа имеют очень большой диапазон измерений, т.е. существует необходимость в перемещении точкой для более эффективного использования имеющегося количества разрядов. В современных процессорах (CPU – Central Processing Unit) имеются дополнительные блоки выполнения арифметических операций и вычисления основных математических функций, их еще называют блоками чисел с плавающей точкой FPU (Floating Point Unit) или NPX (Numeric Processor eXtension – числовое расширение процессора). Ранее в предыдущих процессорах этот блок устанавливался дополнительно в виде математического сопроцессора. Сопроцессор поддерживает 16-, 32- и 64-битные целые числа, 32-, 64-, 80-битные числа с плавающей точкой (FP) и 18-значные числа в двоично-десятичном формате (BCD).

назад далее

6. (Женя!) Для представления чисел

Для представления чисел в форме с плавающей точкой в ЭВМ используется две группы цифр - мантисса M и порядок P. В общем виде это представление может быть выражено, как:

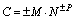(2.4)

где С – представляемое число, а N – основание системы счисления.

Пример 2.9. Представление десятичных чисел с плавающей точкой

Числа, указанные в примере 2.8 могут быть представлены в следующем виде.

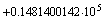
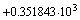
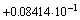
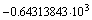
Пример показывает, что представление с помощью мантиссы и порядка, позволяет отображать огромные диапазоны чисел. Ответ на вопрос, какой же диапазон значащих чисел D можно отобразить с помощью m разрядной мантиссы и p разрядного порядка в системе счисления с основанием N дает следующее выражение:

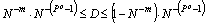(2.5)

Очень красноречивым является пример, приведенный, где при N=2, m=22 иp=10 диапазон чисел примерно простирается от 10^-300 до 10³⁰⁰. Для сравнения количество секунд, которые прошли с момента образования планеты Земля, составляет всего около 10¹⁸ секунд.

Если 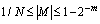, то старший разряд представляемого числа отличен от нуля, такое число называется нормализованным. Именно нормализованные числа хранятся в ЭВМ. В примере 2.9 все числа, кроме второго – нормализованные.

назад далее

7. (Маша!) При рассмотрении систем

При рассмотрении систем счисления в п. 2.1 следовало бы привести еще и двоично-десятичную систему счисления (BCD). Однако в большинстве учебников ее выделяют в качестве обособленной формы представления информации в ЭВМ, поэтому мы сделаем тоже самое. Особенность BCD состоит в том, что десятичные числа записываются двоичными тетрадами. При обработке больших объемов информации, например, при анализе статистических и экономических данных в ЭВМ приходиться производить огромное количество преобразований из двоичного представления в десятичное и обратно. Для этой цели, как уже отмечалось, применяются специальные блоки FPU или NPX. Точка в BCD представлении числа, обычно имеет фиксированное место. Значение знака числа отмечается двоичным кодом (тетрадой), отличным от используемых в BCD. Например, знак «+» имеет значение тетрады «1100», а «-» - «1101».

Пример 2.10. Двоично-десятичное представление чисел.

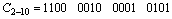
МАШАААА!!!! ЗДЕСЬ НЕТ ОДНОЙ ФОРМУЛЫ. У МЕНЯ НЕ ОТКРЫВАЕТСЯ. ПОСМОТРЕТЬ В: http://marshal-group.com/pri-rassmotrenii-sistem.html

назад далее