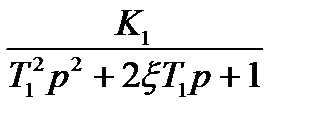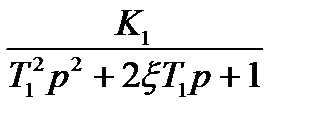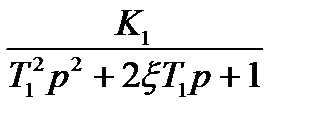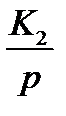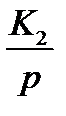В этом случае характеристическое уравнение разомкнутой системы имеет 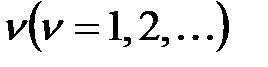 нулевых корней, а сама система является астатической
нулевых корней, а сама система является астатической 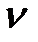 -го порядка.
-го порядка.
Передаточная функция такой системы выглядит следующим образом
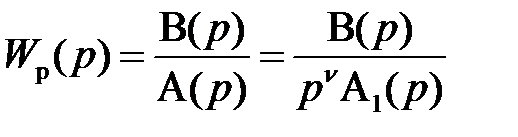 . (10.6)
. (10.6)
Здесь характеристический полином 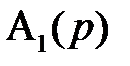 имеет порядок
имеет порядок 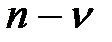 , что обеспечивается равенством нулю последних
, что обеспечивается равенством нулю последних 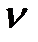 коэффициентов полинома А(р):
коэффициентов полинома А(р):
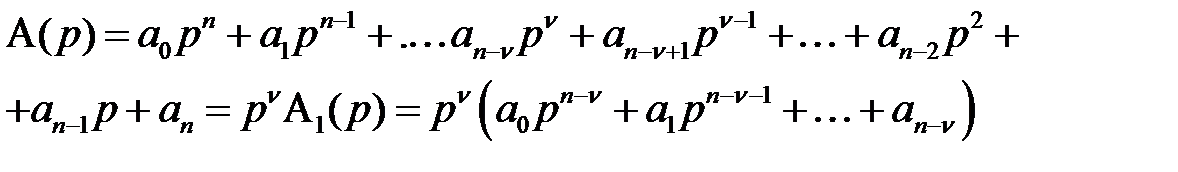
К примеру, для n = 5 при а4 = а5 = 0 т.е. 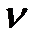 = 2 получим
= 2 получим
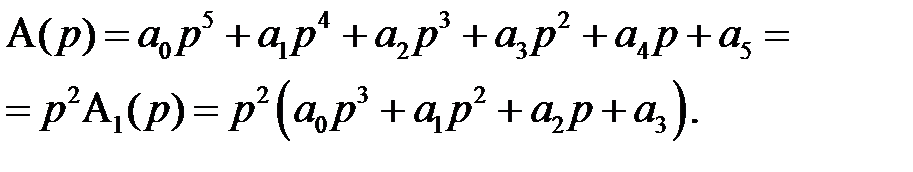 для неустойчивой разомкнутой САР. оси.
для неустойчивой разомкнутой САР. оси.
е!)тельных и 1 системы.тельных преходов
Если в (10.6) подставить 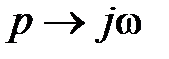 , то из получившегося выражения можно усмотреть, что при
, то из получившегося выражения можно усмотреть, что при 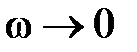 АФХ разомкнутой системы Wp
АФХ разомкнутой системы Wp 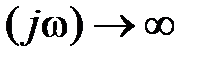 . Следовательно, критерий Найквиста, требующий, чтобы Wp
. Следовательно, критерий Найквиста, требующий, чтобы Wp 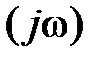 начиналась на действительной оси, для разомкнутой системы, находящейся на границе устойчивости, в обычном, вышеприведенном, виде применять нельзя. Поэтому, (без доказательства) воспользуемся следующим приемом. АФХ разомкнутой САР Wp
начиналась на действительной оси, для разомкнутой системы, находящейся на границе устойчивости, в обычном, вышеприведенном, виде применять нельзя. Поэтому, (без доказательства) воспользуемся следующим приемом. АФХ разомкнутой САР Wp 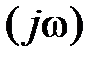 дополним дугой бесконечно большого радиуса с угловым размером
дополним дугой бесконечно большого радиуса с угловым размером 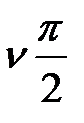 (тем самым «сажая» начало Wp
(тем самым «сажая» начало Wp 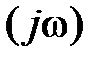 на действительную ось) и уже к этой кривой применим критерий Найквиста. При этом следует иметь в виду, что определять устойчивость или неустойчивость разомкнутой САР надо будет по расположению корней относительно мнимой оси не характеристического уравнения А(р) = 0, а уравнения А1(р) = 0. Например, если уравнение А1(р) = 0 имеет m правых корней, т.е. разомкнутая САР неустойчива, то в замкнутом состоянии САР будет устойчива, если при изменении частоты
на действительную ось) и уже к этой кривой применим критерий Найквиста. При этом следует иметь в виду, что определять устойчивость или неустойчивость разомкнутой САР надо будет по расположению корней относительно мнимой оси не характеристического уравнения А(р) = 0, а уравнения А1(р) = 0. Например, если уравнение А1(р) = 0 имеет m правых корней, т.е. разомкнутая САР неустойчива, то в замкнутом состоянии САР будет устойчива, если при изменении частоты 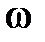 от 0 до ∞ АФХ разомкнутой САР Wp
от 0 до ∞ АФХ разомкнутой САР Wp 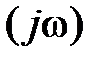 , дополненная дугой
, дополненная дугой 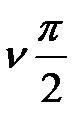 бесконечно большого радиуса, охватывает точку (1; j0) в положительном направлении
бесконечно большого радиуса, охватывает точку (1; j0) в положительном направлении 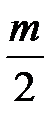 раз.
раз.
Заметим, что и здесь критерий Найквиста можно применять в формулировке Я. З. Ципкина.
На рис. 10.7 приведены Wp 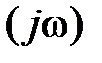 трех различных систем с порядком астатизма
трех различных систем с порядком астатизма 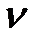 =1,
=1, 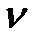 =2 и
=2 и 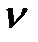 =3. Пусть во всех трех случаях разомкнутые системы устойчивы, т.е. их характеристические уравнения А1(р) = 0 содержат только левые корни.
=3. Пусть во всех трех случаях разомкнутые системы устойчивы, т.е. их характеристические уравнения А1(р) = 0 содержат только левые корни.
Определим устойчивость этих систем в замкнутом состоянии.
Из рис. 10.7 видно, что при 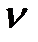 =1
=1 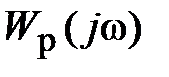 с дополнительной дугой
с дополнительной дугой
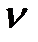 =2 =2 |
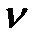 =1 =1 |
Wp(j 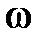 ) ) |
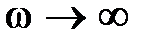 = = |
Wp(j 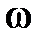 ) ) |
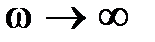 = = |
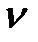 =3 =3 |
Wp(j 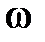 ) ) |
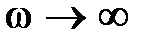 = = |
Рис.10.7. Wp 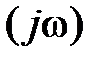 , дополненные дугами бесконечно
, дополненные дугами бесконечно
большого радиуса 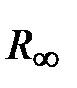 для трех различных систем.
для трех различных систем.
углового размера 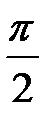 , начинаясь на действительной оси, с ростом частоты не охватывает точку (1, j0). Следовательно, при устойчивой разомкнутой САР система в замкнутом состоянии устойчива.
, начинаясь на действительной оси, с ростом частоты не охватывает точку (1, j0). Следовательно, при устойчивой разомкнутой САР система в замкнутом состоянии устойчива.
При 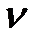 =2
=2 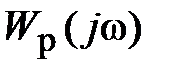 с дополнительной дугой углового размера
с дополнительной дугой углового размера 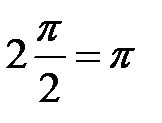 и радиуса
и радиуса 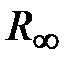 охватывает точку (-1, j0), что приводит к неустойчивости системы в замкнутом состоянии.
охватывает точку (-1, j0), что приводит к неустойчивости системы в замкнутом состоянии.
При 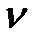 =3 видно, что Wp
=3 видно, что Wp 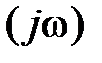 с дополнительной дугой углового размера
с дополнительной дугой углового размера 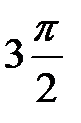 и радиуса
и радиуса 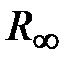 имеет по Цыпкину одним положительной и один отрицательный переходы, это означает устойчивость замкнутой САР при устойчивой разомкнутой системе.
имеет по Цыпкину одним положительной и один отрицательный переходы, это означает устойчивость замкнутой САР при устойчивой разомкнутой системе.
АФЧХ замкнутой САУ и АФЧХ ее разомкнутого контура связаны зависимостью
(10.7)
Отсюда следует, что передаточная функция разомкнутого контура и характеристический полином D(jω) замкнутой передаточной функции связаны между собой соотношением
(10.8)
Главной отличительной особенностью критерия Найквиста является возможность исследования устойчивости замкнутой САУ по виду амплитудно-фазовой частотной характеристики ее разомкнутого контура, которую строить гораздо проще. Кроме того, этот критерий позволяет определять устойчивость по экспериментально снятым частотным характеристикам.
Существует две формулировки критерия Найквиста в зависимости от того, устойчива или неустойчива САУ в разомкнутом состоянии:
1. Если в разомкнутом состоянии САУ устойчива, то для того чтобы она была устойчива в замкнутом состоянии, необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика ее разомкнутого контура не охватывала точку с координатами (–1;j0).
2. Неустойчивая в разомкнутом состоянии САУ в замкнутом состоянии является устойчивой, если число пересечений амплитудно-фазовой частотной характеристики отрицательной вещественной полуоси левее точки (–1;j0) сверху вниз будет на m/2 больше, чем число пересечений снизу вверх (m – число корней характеристического уравнения разомкнутой САУ, расположенных в правой полуплоскости).
На рисунке 10.8а,б изображены АФЧХ устойчивых САУ в замкнутом состоянии для первой и второй формулировок критерия соответственно.
Рисунок 10.8
Критерий Найквиста позволяет судить об устойчивости замкнутой САУ по АФЧХ разомкнутой системы W(jw). Годограф W(jw) получают аналитически или экспериментально. В зависимости от свойств разомкнутой САУ годограф может иметь различный вид. В связи с этим при анализе устойчивости замкнутой САУ различают три типовых случая состояния (устойчивости) разомкнутой САУ.
Первый случай охватывает САУ, устойчивые в разомкнутом состоянии. Таким свойством обладают статические САУ, а годограф W(jw) совместно с осью вещественных чисел образует замкнутый контур (см. рисунки 10.9 и 10.10). Начинается (w = 0) годограф на вещественной положительной полуоси в точке с координатами (K, j0), где K – коэффициент передачи (усиления) разомкнутой САУ, а заканчивается в начале координат (w = ¥).
В первом случае для устойчивости замкнутой САУ необходимо и достаточно, чтобы годограф разомкнутой САУ не охватывал точку с координатами (-1; 0j), которую называют критической. Годограф 1 на рисунке 10.9 принадлежит устойчивой САУ, 2 – неустойчивой, 3 – САУ, находящейся на границе устойчивости. На рисунке 10.10 показан годограф W(jw) устойчивой САУ, имеющий вид клювообразной кривой. Этот годограф пересекает отрицательную действительную полуось левее критической точки. При этом количество положительных (сверху вниз) переходов годографа через полуось левее критической точки равно количеству отрицательных (снизу вверх) переходов. Это означает, что годограф действительно не охватывает критическую точку. На рисунке 10.10 отрицательный и положительный переходы отмечены знаками "-" и "+".
Второй случай охватывает нейтральные САУ, т.е. находящиеся в разомкнутом состоянии на границе устойчивости. Таким свойством обладают астатические САУ, а годограф W(jw) не может образовать замкнутого контура ни с одной из осей, так как начинается (w = 0) в бесконечности. Эту особенность называют разрывом годографа.
Во втором случае критерий Найквиста формулируется следующим образом: для устойчивости замкнутой САУ необходимо и достаточно, чтобы годограф разомкнутой САУ, дополненный на участке разрыва дугой бесконечно большого радиуса, не охватывал критическую точку.
На рисунке 10.11 показаны годографы 1 и 2 САУ с астатизмом первого порядка (v = 1). Годограф 1 принадлежит устойчивой, а годограф 2 – неустойчивой системе.
Клювообразный годограф на рисунке10.5 принадлежит устойчивой САУ с астатизмом второго порядка (v = 2).
Третий случай охватывает САУ, неустойчивые в разомкнутом состоянии. Характеристический полином таких систем A(s) имеет l "правых" корней, т.е. корней с положительной вещественной частью.
В третьем случае, наиболее общем, критерий Найквиста формулируется следующим образом: для устойчивости замкнутой САУ необходимо и достаточно, чтобы годограф разомкнутой САУ охватывал критическую точку l/2 раз в положительном направлении (против часовой стрелки).
Анализ устойчивости САУ с годографом сложной формы, например изображенным на рисунке 10.12, упрощается при использовании правила переходов. Критерий Найквиста формулируется при этом следующим образом: замкнутая САУ устойчива, если разность между количеством положительных и отрицательных переходов годографа разомкнутой системы W(jw) через отрезок вещественной оси от -¥ до критической точки равна l/2. Годограф может начинаться на указанном отрезке при w = 0 (рисунок 10.12) или заканчиваться при w = ¥. В этом случае считают, что годограф совершает полперехода. Так, например, годограф, изображенный на рисунке, совершает один положительный переход, отмеченный знаком "+", и половину отрицательного перехода, отмеченного знаком "-". Разность названных переходов равна +1/2. Замкнутая САУ будет устойчивой, если l/2 = 1/2.
Если характеристический полином разомкнутой системы A(s) кроме корней с вещественной частью имеет нулевые и чисто мнимые корни, то на участках разрыва годограф W(jw) должен быть дополнен дугой бесконечно большого радиуса.
В данной работе необходимо:
Оценить устойчивости линейной системы автоматического управления по критерию Найквиста и выполнить расчеты задания № 1
Задание №1
1. Определить устойчивость автоматической системы с помощью критерия Найквиста, для системы со следующей структурной схемой
| Вариант | к1 | к2 | к3 | к4 | Т1 | Т2 | Т3 | Т4 |
| | | 0,58 | | | 0,1 | 0,5 | | 4,7 |
| | | 0,34 | | 1,5 | 0,1 | 0,6 | | 1,5 |
| | | 0,69 | | 7,6 | 0,1 | 0,7 | | 6,4 |
| | | 0,33 | | 8,6 | 0,1 | | 0,5 | 3,8 |
| | | 0,10 | | 4,5 | 0,1 | 1,0 | | |
2. Определить устойчивость системы автоматического управления с помощью критерия Найквиста со следующей структурной схемой
К1= 120 Т1= 0,25 ξ=0,05
3. Определить устойчивость системы автоматического управления с помощью критерия Найквиста со следующей структурной схемой
К1= 48 Т1= 0,47 ξ=0,5 К2=10
4. Определить устойчивость системы автоматического управления с помощью критерия Найквиста со следующей структурной схемой
| Вариант | к1 | к2 | Т1 | Т2 | ξ |
| | | | 0,1 | 2,56 | 0,5 |
| | | | 0,23 | 5,63 | 0,6 |
| | | | 0,14 | 4,5 | 0,7 |
| | | | 0,19 | 4,7 | |
| | | | 0,42 | 1,28 | 1,0 |
5. Определить устойчивость системы автоматического управления с помощью критерия Найквиста со следующей структурной схемой
| Вариант | к1 | к2 | к3 | Т1 | Т2 | ξ |
| | | | 0,0021 | 0,1 | 2,56 | 0,5 |
| | | | 0,008 | 0,23 | 5,63 | 0,6 |
| | | | 0,004 | 0,14 | 4,5 | 0,7 |
| | | | 0,4 | 0,19 | 4,7 | |
| | | | 0,18 | 0,42 | 1,28 | 1,0 |
6. Определить устойчивость системы автоматического управления с помощью критерия Найквиста со следующей структурной схемой
| Вариант | к1 | к2 | к3 | к4 | Т3 |
| | | | 0,0021 | | 2,56 |
| | | | 0,008 | | 5,63 |
| | | | 0,004 | | 4,5 |
| | | | 0,4 | | 4,7 |
| | | | 0,18 | | 1,28 |
7. Определить устойчивость системы автоматического управления с помощью критерия Найквиста со следующей структурной схемой
| Вариант | к1 | к2 | Т1 | Т2 |
| | | | 0,8 | 2,0 |
| | | | 0,7 | 5,63 |
| | | | 0,15 | 4,5 |
| | | | 1,2 | 4,7 |
| | | | | 1,28 |
8. Определить устойчивость системы автоматического управления с помощью критерия Найквиста со следующей структурной схемой
| Вариант | к1 | к2 | к3 | К4 | Т4 | Т1 | ξ |
| | | | 0,21 | 11,02 | 0,1 | 2,56 | 0,5 |
| | | | 0,08 | 0,98 | 0,23 | 5,63 | 0,6 |
| | | | 0,54 | 4,23 | 0,14 | 4,5 | 0,7 |
| | | | 0,14 | 4,3 | 0,19 | 4,7 | |
| | | | 0,38 | 4,1 | 0,42 | 1,28 | 1,0 |
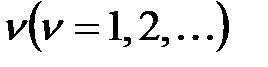 нулевых корней, а сама система является астатической
нулевых корней, а сама система является астатической 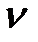 -го порядка.
-го порядка.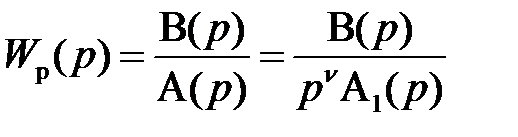 . (10.6)
. (10.6)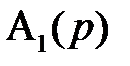 имеет порядок
имеет порядок 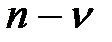 , что обеспечивается равенством нулю последних
, что обеспечивается равенством нулю последних 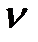 коэффициентов полинома А(р):
коэффициентов полинома А(р):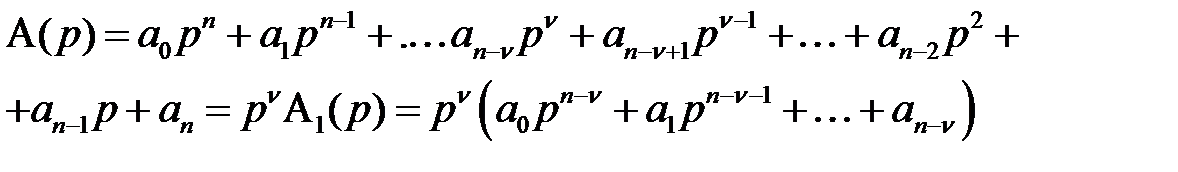
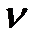 = 2 получим
= 2 получим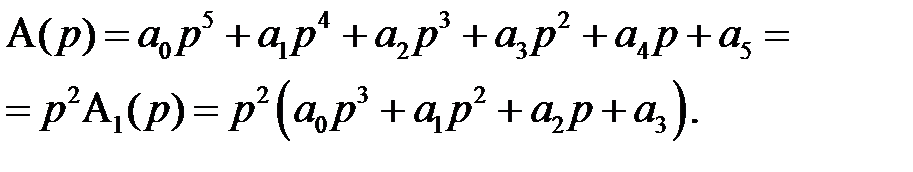 для неустойчивой разомкнутой САР. оси.
для неустойчивой разомкнутой САР. оси.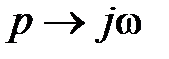 , то из получившегося выражения можно усмотреть, что при
, то из получившегося выражения можно усмотреть, что при 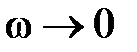 АФХ разомкнутой системы Wp
АФХ разомкнутой системы Wp 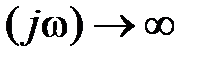 . Следовательно, критерий Найквиста, требующий, чтобы Wp
. Следовательно, критерий Найквиста, требующий, чтобы Wp 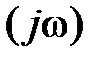 начиналась на действительной оси, для разомкнутой системы, находящейся на границе устойчивости, в обычном, вышеприведенном, виде применять нельзя. Поэтому, (без доказательства) воспользуемся следующим приемом. АФХ разомкнутой САР Wp
начиналась на действительной оси, для разомкнутой системы, находящейся на границе устойчивости, в обычном, вышеприведенном, виде применять нельзя. Поэтому, (без доказательства) воспользуемся следующим приемом. АФХ разомкнутой САР Wp 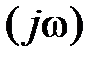 дополним дугой бесконечно большого радиуса с угловым размером
дополним дугой бесконечно большого радиуса с угловым размером 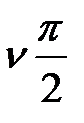 (тем самым «сажая» начало Wp
(тем самым «сажая» начало Wp 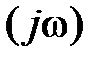 на действительную ось) и уже к этой кривой применим критерий Найквиста. При этом следует иметь в виду, что определять устойчивость или неустойчивость разомкнутой САР надо будет по расположению корней относительно мнимой оси не характеристического уравнения А(р) = 0, а уравнения А1(р) = 0. Например, если уравнение А1(р) = 0 имеет m правых корней, т.е. разомкнутая САР неустойчива, то в замкнутом состоянии САР будет устойчива, если при изменении частоты
на действительную ось) и уже к этой кривой применим критерий Найквиста. При этом следует иметь в виду, что определять устойчивость или неустойчивость разомкнутой САР надо будет по расположению корней относительно мнимой оси не характеристического уравнения А(р) = 0, а уравнения А1(р) = 0. Например, если уравнение А1(р) = 0 имеет m правых корней, т.е. разомкнутая САР неустойчива, то в замкнутом состоянии САР будет устойчива, если при изменении частоты 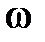 от 0 до ∞ АФХ разомкнутой САР Wp
от 0 до ∞ АФХ разомкнутой САР Wp 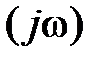 , дополненная дугой
, дополненная дугой 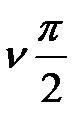 бесконечно большого радиуса, охватывает точку (1; j0) в положительном направлении
бесконечно большого радиуса, охватывает точку (1; j0) в положительном направлении 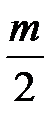 раз.
раз.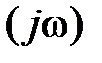 трех различных систем с порядком астатизма
трех различных систем с порядком астатизма 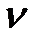 =1,
=1, 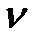 =2 и
=2 и 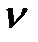 =3. Пусть во всех трех случаях разомкнутые системы устойчивы, т.е. их характеристические уравнения А1(р) = 0 содержат только левые корни.
=3. Пусть во всех трех случаях разомкнутые системы устойчивы, т.е. их характеристические уравнения А1(р) = 0 содержат только левые корни.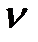 =1
=1 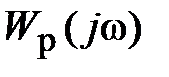 с дополнительной дугой
с дополнительной дугой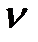 =2
=2 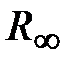
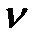 =1
=1 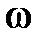 )
) 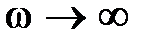 =
= 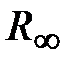
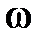 )
) 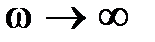 =
= 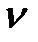 =3
=3 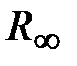
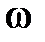 )
) 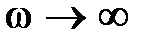 =
= 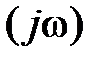 , дополненные дугами бесконечно
, дополненные дугами бесконечно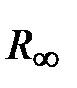 для трех различных систем.
для трех различных систем.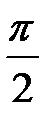 , начинаясь на действительной оси, с ростом частоты не охватывает точку (1, j0). Следовательно, при устойчивой разомкнутой САР система в замкнутом состоянии устойчива.
, начинаясь на действительной оси, с ростом частоты не охватывает точку (1, j0). Следовательно, при устойчивой разомкнутой САР система в замкнутом состоянии устойчива.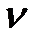 =2
=2 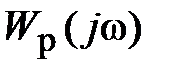 с дополнительной дугой углового размера
с дополнительной дугой углового размера 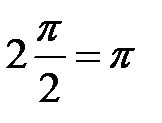 и радиуса
и радиуса 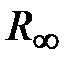 охватывает точку (-1, j0), что приводит к неустойчивости системы в замкнутом состоянии.
охватывает точку (-1, j0), что приводит к неустойчивости системы в замкнутом состоянии.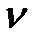 =3 видно, что Wp
=3 видно, что Wp 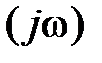 с дополнительной дугой углового размера
с дополнительной дугой углового размера 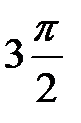 и радиуса
и радиуса 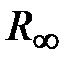 имеет по Цыпкину одним положительной и один отрицательный переходы, это означает устойчивость замкнутой САР при устойчивой разомкнутой системе.
имеет по Цыпкину одним положительной и один отрицательный переходы, это означает устойчивость замкнутой САР при устойчивой разомкнутой системе.