И методов обработки результатов эксперимента

Лабораторная работа №1

ИЗУЧЕНИЕ СТАТИСТИЧЕСКИХ ЗАКОНОМЕРНОСТЕЙ

И МЕТОДОВ ОБРАБОТКИ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА

ЦЕЛЬ РАБОТЫ

Моделирование нормального распределения случайной величи-ны на примере измерения сопротивлений резисторов. Освоение методики статистической обработки результатов прямых измере-ний случайной величины. Получение навыков составления статис-тических рядов и оценки достоверности результатов измерений.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

В данной работе продолжается рассмотрение случайных вели-чин. Случайной величиной здесь является результат измерения со-противления 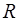одного из резисторов. Несмотря на то, что на мар-кировке резисторов указано одинаковое значение сопротивления (номинал), фактические сопротивления отличаются от указанного номинала.

Представим себе, что мы производим измерения сопротивления резисторов одного номинала, причем число таких измерений (т.е. число обмеренных резисторов) велико и равно 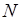. Обозначим ре-зультат одного измерения через ( ).

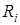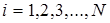Очевидно, что все результаты измерений заключены в пределах интервала от наименьшего значения 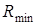до наибольшего :

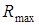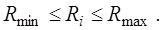(3.1.1)

Разобъем этот интервал на 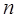равных интервалов , .

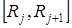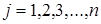Пусть при измерeнии сопротивлений определенное количество 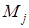результатов попали в интервал 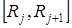. Это будем считать со-бытием. Поскольку количество опытов ограничено, то можем оп-ределить статистическую вероятность 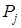такового события, поль-зуясь формулой (3.1.2):

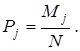(3.1.2)

Иными словами, 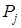представляет собой частоту попадания из-меряемой величины 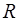в интервал значений 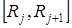. Предполага-ется, что при возрастании числа измерений 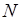величина 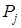стре-мится к определенному пределу. Мы будем считать, что значение 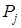существенно не изменится, если число измерений 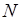удвоится или утроится.

Из определения вероятности следует, что вероятность принятия измеряемой величиной 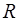какого–либо значения равна 1, поэтому сумма всех вероятностей:

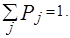(3.1.3)

Говорят, что вероятность нормирована на единицу.

Среднее значение измеряемой величины 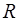определим как:

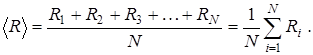(3.1.4)

Выделим внутри суммы 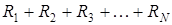слагаемые, попада-ющие в интервал 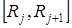, и найдем их сумму, которую обозначим 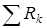. Пусть число слагаемых в этой сумме есть 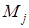, тогда, исполь-зуя определение (3.1.4) можно записать:

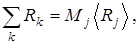(3.1.5)

где 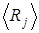– среднее значение величины на интервале .

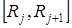Таким образом, выражение (3.1.4) приобретает вид:

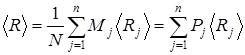. (3.1.6)

Если взять величину интервала 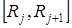достаточно малой, то средним значением 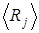на интервале можно считать середину интервала:

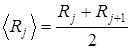. (3.1.7)

Равенство (3.1.6) выполняется тем точнее, чем меньше интер-вал.

Разброс значений случайной величины 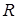около среднего значе-ния 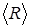характеризуется величиной, называемой дисперсией 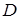. Дисперсия представляет собой средний квадрат отклонения слу-чайной величины 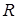от её среднего значения :

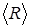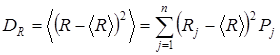. (3.1.8)

Квадратный корень из этой величины называется средним квад-ратичным отклонением :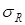

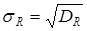. (3.1.9)

Измеряемая нами случайная величина 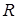может принимать лю-бое значение из интервала 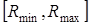, причем заранее нельзя про-считать ее возможные значения. Такую случайную величину назы-вают непрерывной.

Непрерывная случайная величина 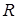определяется заданием ин-тервала 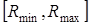, содержащего все возможные значения этой ве-личины, и функции 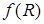, которая называется плотностью вероят-ностей случайной величины 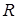(или плотностью распределения ).

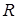Физический смысл 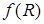следующий. Пусть 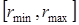– произ-вольный интервал, содержащийся в 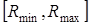. Тогда вероятность того, что 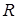окажется в интервале 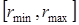, равна интегралу:

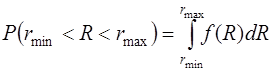. (3.1.10)

Плотность вероятностей 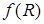должна удовлетворять двум усло-виям, вытекающим из ее свойств:

1.

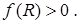
2. 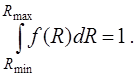(3.1.11)

Нормальной, или гауссовой случайной величиной называется случайная величина, определенная на всей оси 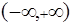и имеющая плотность вероятностей (получено на основе формулы (1.26)):

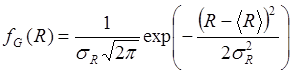, (3.1.12)

где 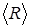– среднее значение, или математическое ожидание слу-чайной величины, 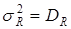- дисперсия, 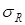- среднеквадратичная ошибка, или стандартное отклонение.

На рис.3.1.1 представлены две нормальные плотности, соответ-ствующие одному среднему 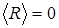и двум различным стандартным отклонениям 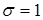и .

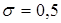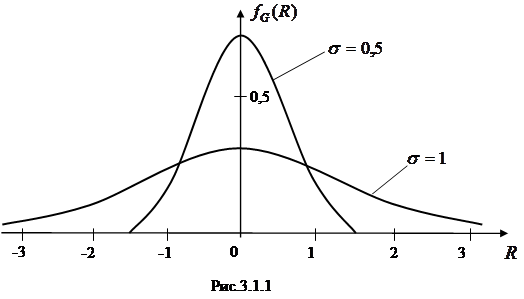График нормальной плотности симметричен относительно 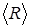. Это означает равновероятность отклонения результатов как вправо, так и влево относительно среднего значения. График достигает максимума при 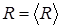, т.е. наиболее вероятным является среднее значение 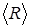. Малые отклонения от среднего более вероятны, чем большие.

Нормальные случайные величины очень часто встречаются при исследовании самых различных по своей природе вопросов. Напри-мер, ошибка измерения, как правило, представляет собой нормаль-ную случайную величину.

Нетрудно вычислить, что для нормального распределения всегда выполняется следующее равенство:

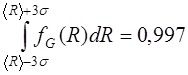. (3.1.13)

Вероятность 0,997 настолько близка к единице, что иногда вы-ражение (3.1.13) интерпретируют так. При одном испытании прак-тически невозможно получить значение случайной величины 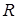, отличающееся от 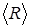более, чем на 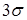– правило “трех сигм”. Дру-гими словами, практически все достоверные результаты помеща-ются в интервале 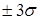от среднего значения (математического ожидания). Если полученный результат не находится в указанном интервале 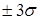, то, вероятнее всего, такой результат является промахом и в дальнейших расчетах не учитыватся.

Результаты измерений сопротивлений резисторов можно пред-ставить графически. Для этого разобьем интервал возможных значе-ний 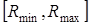на 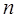равных малых конечных интервалов 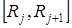. В прямоугольной системе координат составим диаграмму по следую-щему принципу: на оси абцисс отметим точки 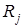и построим прямо-угольники с основанием, равным длине интервала 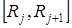и высо-той, равной числу результатов 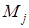, попадающих в этот интервал. Такая диаграмма называется гистограммой. Она имеет вид ступен-чатой фигуры, пример гистограммы приведен на рис. 3.1.2.

Очевидно, что высота отдельного прямоугольника из гистограм-мы пропорциональна вероятности обнаружить резистор из числа измеренных, сопротивление которого попадает в интервал значе-ний .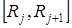

Если увеличить число измерений 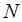и уменьшить ширину ин-тервала 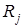, равную 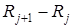, то огибающая гистограммы перейдет в плавную линию.Эта линия является графиком некоторой функции 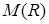, что также показано на рис.3.1.2.