Лекція 4. Задачі лінійної алгебри
4.1 Введение. Численные методы.
Линейная алгебра – раздел алгебры, изучающий объекты линейной природы (матрицы, векторы), системы линейных уравнений (СЛАУ). Лекция посвящена изложению методов решения СЛАУ. Задачи линейной алгебры основываются на работе с матрицами. Типичными задачами являются вычисление определителя матрицы, нахождение обратной матрицы, а также задачи, связанные с решением СЛАУ. Нахождение определителя и обратной матрицы при этом являются базовыми задачами.
С линейной алгеброй тесно связаны численные методы (вычислительные методы) – методы решения математических задач в численном виде.
Численные методы направлены на:
– решение СЛАУ;
– проведение интерполирования и аппроксимации;
– численное интегрирование;
– решение задач оптимизации;
– численное решение систем нелинейных уравнений;
– численное решение ОДУ.
Использование численных методов как правило связано с построением и исследованием математических моделей систем и процессов, сопряженной с использованием аппаратных возможностей современных ЭВМ.
Этапы численного решения задачи на ЭВМ:
1) постановка задачи;
2) разработка метода или алгоритма решения задачи;
3) реализация разработанного метода или алгоритма в виде компьютерной программы (получение компьютерной модели);
4) отладка (тестирование) программы;
5) проведение вычислений и анализ результатов.
Постановка задачи заключается в построении математической модели (в получении системы уравнений).
Когда задача не может быть решена аналитическим путем, возникает необходимость разработки численных методов решения, при которых производится лишь выполнение арифметических операций сложения, вычитания, умножения и деления. Например, вычисление интеграла сводится к вычислению суммы (площадей под кривой) и т.д. Разработанный метод может быть представлен в виде алгоритма – последовательности операций (шагов), позволяющих получить требуемый результат.
4.2 Погрешность в численных методах.
При использовании численных методов (различных итерационных их реализаций) возникает погрешность вычислений.
Выделяют 4 источника погрешности результата решения вычислительной задачи [6]:
1) погрешность математической модели;
2) погрешность исходных данных;
3) погрешность численного метода;
4) погрешность округления.
Погрешность мат. модели зависит от допущений, сделанных при построении модели. Например, замена реальной зависимости линейной зависимостью (путем разложения в ряд Тейлора). Погрешность мат. модели обуславливает адекватность модели системе – чем погрешность меньше, тем модель более адекватна (в большей степени соответствует действительности).
Погрешность исходных данных обуславливается неточностью измерений или невозможностью проведения достаточно точных измерений. Такая погрешность также возникает при невозможности представления значений замеров конечной десятичной дробью. В этом случае мы вынуждены прибегать к округлению. Погрешность исходных данных также называют неустранимой погрешностью.
Погрешность численных методов связана с заменой точных операторов приближенными: интеграла – суммой, функции – полиномом, бесконечного итерационного процесса – конечным числом итераций (обусловлено вычислительными возможностями или требованиями к точности). Большая погрешность снижает ценность и достоверность получаемого результата, малая погрешность – обуславливает экспоненциальный рост объема вычислений.
Погрешность, возникнув, распространяется в процессе вычислений. При этом как правило, происходит накопление различных погрешностей, что ставит под сомнений конечный результат вычислений (уменьшается его достоверность).
Выделяют такие погрешности вычислений:
– абсолютная погрешность:
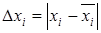, (4.1)
где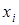 
– фактическое (точное) значение, 
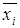– оценочное (приближенное) значение, а 
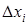– абсолютная погрешность приближенного значения.
– относительная погрешность – отношение абсолютной погрешности к приближенному значению:
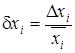. (4.2)
Существуют утверждения, что подавляющее большинство всех расчетных математических задач приходится на решение СЛАУ – по причине осуществления дискретизации и линеаризации исследуемых явлений, систем или процессов в моделях (математических).
Поскольку ранее было отмечено, что численные методы сводятся к выполнению арифметических операций, возникает необходимость в нахождении абсолютных и относительных погрешностей операций сложения, вычитания, умножения и деления.
Для этого введем следующие обозначения:
– 
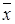и 
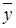– приближенные значения чисел 
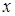и 
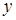, соответственно;
– 
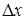и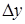 
– соответствующие абсолютные погрешности: 
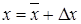, а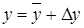 
;
– 
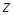– результат выполнения арифметической операции.
Получим выражения для вычисления абсолютных значений погрешностей при выполнении арифметических операций.
Для операции сложения абсолютная погрешность суммы равна сумме абсолютных погрешностей слагаемых:
;
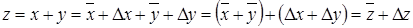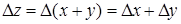. (4.3)
Для операции вычитания выражение абсолютной погрешности получают аналогичным образом:
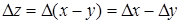. (4.4)
Для операции умножения:
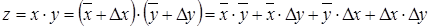, где выражением 
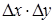обычно пренебрегают. Тогда для операции произведения получим следующее выражение абсолютной погрешности:
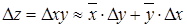. (4.5)
Для вычисления погрешности операции деления выполняют разложение функции в ряд Тейлора:
.
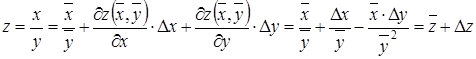Абсолютная погрешность деления:
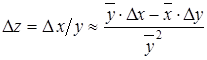. (4.6)
Для относительных погрешностей получим следующие выражения:
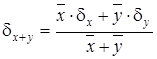. (4.7)
Для операции вычитания:
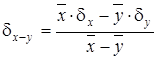. (4.8)
Для операции умножения:
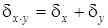. (4.9)
Для операции деления:
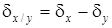. (4.10)
4.3 Численные методы решения СЛАУ.
Выделяют два класса методов решения СЛАУ – прямые и итерационные:
– прямые методы позволяют получить решение за конечное число арифметических операций (шагов); прямые методы также называют точными методами; распространенными прямыми методами являются метод Крамера, метод обратной матрицы и метод Гаусса;
– итерационные методы, позволяющие получить точное решение лишь за бесконечное число шагов (итераций), поэтому на практике получают приближенные решения, удовлетворяющие заданной погрешности; примеры методов – метод Якоби, метод Зейделя.
Существуют различные программные комплексы, позволяющие решать СЛАУ: MathCAD, MATLAB, Mathematica и др.
Чтобы успешно пользоваться на практике различными численными методами, важно ориентироваться в их специфике.
Решение СЛАУ есть решение систем вида
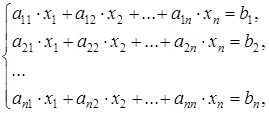(4.1)
которые также представляются векторно-матричными уравнениями вида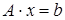 
, где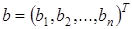 
– вектор свободных членов, 
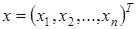– вектор неизвестных (вектор-решение) с вещественными координатами, а 
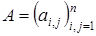– вещественная 
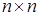-матрица коэффициентов системы. Эффективность различных методов решения СЛАУ во многом зависит от структуры матрицы: симметричности, заполненности, расположения ненулевых элементов.
Прямой метод Крамера – удобное средство аналитического решения СЛАУ небольшой размерности. Число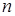 
(размерность системы) – причина, по которой метод Крамера неприемлем на практике при достаточно больших 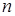. Асимптотика метода Крамера составляет 
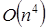. Такая же асимптотика и у метода обратной матрицы. Наилучшая асимптотика у метода Гаусса – 
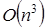, что обусловило распространенность его машинных реализаций.
4.3.1 Прямые методы. Метод Крамера.
Был создан швейцарским математиком Габриелем Крамером в 1750 г.
Для системы из 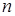линейных алгебраических уравнений с 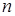неизвестными с определителем матрицы системы 
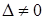решение записывается в виде
,
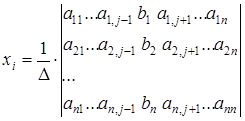где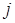 
-й столбец заменяется столбцом свободных членов.
Решение СЛАУ методом Крамера может быть представлено в виде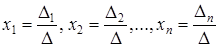 
. Таким образом, при решении СЛАУ методом Крамера необходимо высчитать 
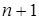определитель размерности .
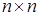Вычислительная сложность метода Крамера составляет 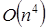, поскольку асимптотическая сложность вычисления определителя матрицы методом Гаусса составляет 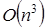. В связи с этим машинная реализация метода Крамера не пользуется широкой популярностью – поскольку альтернативный метод решения СЛАУ (метод Гаусса) имеет лучшую асимптотику – 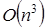. В 2010 г, однако, было показано, что метод Крамера может быть реализован с асимптотической сложностью 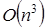, что ставит его в один ряд с методом Гаусса.
Пример решения СЛАУ методом Крамера.
Пусть имеем СЛАУ вида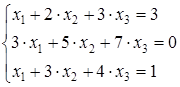 
.
1. Представим СЛАУ в матричном виде:
,
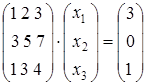где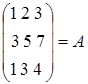 
– матрица коэффициентов при неизвестных, 
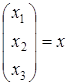и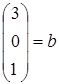 
– вектор неизвестных и вектор свободных членов, соответственно.
2. Посчитаем определитель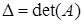 
для матрицы коэффициентов при неизвестных 
:
,
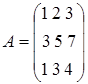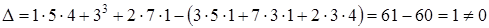что свидетельствует о согласованности системы и о существовании единственного ее решения.
3. Вычислим аналогичным образом также определители матриц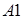 
, 
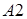и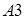 
, полученных путем замещения 1-го, 2-го и 3-го столбцов матрицы 
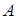, соответственно:
, 
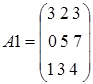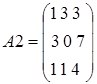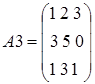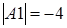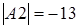и 
.
, 
и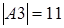 
.
4. Получим решение СЛАУ:
, 
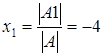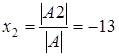и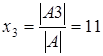 
.
Порядок решения СЛАУ методом Крамера в MathCAD следующий:
1) ввод матрицы коэффициентов 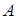при неизвестных;
2) ввод вектора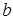 
свободных членов;
3) вычисление определителя матрицы: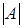 
;
4) ввод 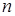матриц, полученных на основе матрицы 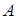, в которых 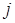-е столбцы ( 
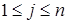) заменены вектором ;
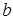5) ввод формул для вычисления элементов вектора неизвестных (корней):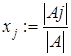 
;
6) вывод значений корней: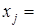 
.
4.3.2 Прямые методы. Метод Гаусса.
Суть метода Гаусса – последовательное исключение неизвестных.
Этот метод также называют методом Гаусса-Жордана.
Рассмотрим технологию получения вектора неизвестных 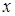из матрицы 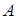и вектора свободных членов .
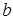Говорят также, что названный алгоритм приводит матрицу 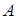к единичной матрице.
В алгоритме решения СЛАУ методом Гаусса выделяют 2 этапа (прямой ход и обратный ход):
– прямой ход – систему приводят к ступенчатому или треугольному виду: сначала (на 1-м шаге прямого хода) исключается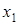 
из 2-го, 3-го,…, 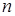-го уравнений системы; затем – 
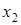– из 3-го, 4-го,…, 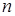-го уравнений системы, и т.д.;
– обратный ход – выражение базисных переменных через небазисные: начиная с последнего уравнения, выражают
Реализация соответствующего алгоритма заключается в последовательном приведении системы вида (4.1) к треугольному виду путем исключения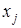 
.
Рассмотрим реализацию прямого хода:
– на первом шаге прямого хода модифицируем 2-е, 3-е,…, 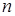-е уравнения системы путем вычитания из них первого уравнения, умноженного на коэффициент при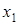 
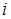-го уравнения и деленное на коэффициент при 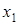1-го уравнения, где 
;
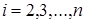– на втором шаге прямого хода вычтем из 3-го, 4-го,…, 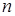-го уравнений системы второе (модифицированное на 1-м шаге) уравнение, умноженное на коэффициент при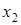 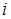-го уравнения и деленное на коэффициент при 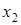2-го уравнения, где 
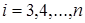, и т.д.
Таким образом, для реализации прямого хода метода Гаусса понадобится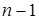 
итераций, в результате чего система будет приведена к треугольному (ступенчатому) виду.
Формализуем (поясним) сказанное:
– по выполнении первого шага прямого хода система (4.1) будет приведена к следующему виду:
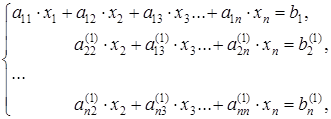, (4.2)
где верхний индекс (1) есть номер шага – порядковый номер модификации уравнения. Коэффициенты при неизвестных, а также элементы вектора 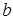при этом вычисляются по следующим формулам:
; 
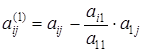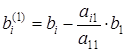, где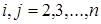 
;
– по выполнении 2-го шага прямого хода получим новую систему (4.3), модифицированную относительно (4.2):
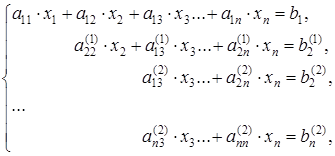, (4.3)
где коэффициенты при неизвестных и элементы вектора правых частей вычисляются следующим образом:
; 
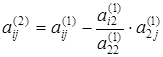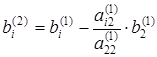, где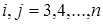 
.
Тогда на заключительном (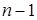 
-м) этапе прямого хода получим систему ступенчатого вида (4.4):
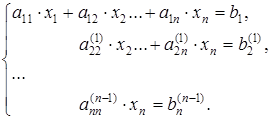, (4.4)
Таким образом, обобщенные формулы вычисления коэффициентов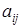 
и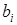 
будут иметь следующий вид:
; 
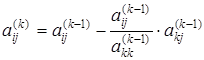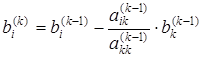, где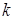 
– порядковый номер шага прямого хода алгоритма: 
.
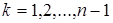Вычисление значений неизвестных произведем при обратном ходе метода Гаусса:
; 
; 
.
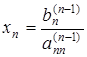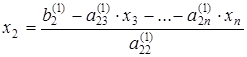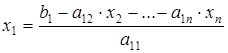Обобщенная формула для обратного хода метода Гаусса имеет следующий вид:
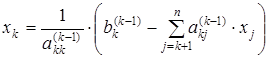, (4.5)
где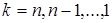 
.
Алгоритм решения СЛАУ методом Гаусса, представленный в виде псевдокода, имеет следующий вид [5]:
Листинг 4.1 – Псевдокод алгоритма решения СЛАУ методом Гаусса
// прямой ход:
1. для ,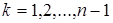
2. для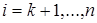 
:
3. 
, 
;
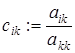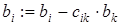4. для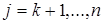 
:
5. 
.
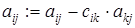// обратный ход:
6. 
;
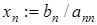7. для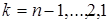 
:
8. 
.
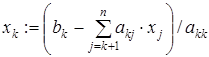Комментарии к приведенному алгоритму:
– на вход подаются квадратная матрица коэффициентов при неизвестных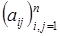 
, а также вектор свободных членов 
;
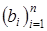– прямой ход алгоритма состоит в реализации шагов 1 – 5 алгоритма, а обратный ход – шагов 6 – 8, в результате выполнения которых получим вектор-решение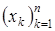 
.
Программная реализация рассмотренного алгоритма приведена в листинге 4.2.
Листинг 4.2 – Программный код реализации алгоритма
void g_solve(vector<vector<float> > &mx) {
int i,j,k;
float tmp; // to contain intermediate coefficient
// direct order
for(i=0; i<m; ++i) {
tmp = mx[i][i];
for(j=m; j>=i; j--) {
mx[i][j] /= tmp;
}
for(j=i+1; j<m; ++j) {
tmp = mx[j][i];
for(k=m; k>=i; k--) {
mx[j][k] -= tmp*mx[i][k];
}
}
}
// reverse order
x[m-1] = mx[m-1][m];
for(i=m-2; i>=0; i--) {
x[i] = mx[i][m];
for(j=i+1;j<m;++j) {
x[i] -= mx[i][j]*x[j];
}
}
}
На вход функции листинга 4.2 подается матрица размером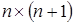 
.
Например, если на вход подать матрицу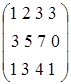 
, то в результате завершения прямого хода алгоритма решения СЛАУ методом Гаусса эта матрица будет преобразованная к ступенчатому виду: 
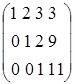. Стоит отметить, что три вложенных цикла алгоритма задают результирующую асимптотику 
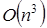. По завершении обратного хода алгоритма получим вектор решений 
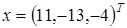. Асимптотика обратного хода при этом составляет 
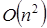– по причине 2-х вложенных циклов.
При оценке вычислительной асимптотической сложности алгоритмов обычно выполняют подсчет операций умножения и деления, поскольку они более ресурсоемки по сравнению с операциями сложения и вычитания. Для метода Гаусса такая оценка представляется выражением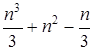 
[5].
Порядок решения СЛАУ методом Гаусса в MathCAD следующий:
1) формирование матрицы коэффициентов при неизвестных и вектора свободных членов:
; 
;
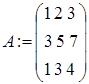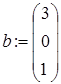2) вычисление определителя матрицы: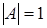 
;
3) использование функции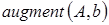 
для формирования расширенной матрицы – матрицы 
: 
;
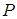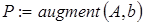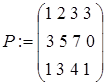
4) использование функции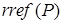 
– формирование ступенчатой матрицы: 
;
;
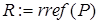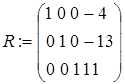5) получение вектора неизвестных: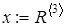 
; 
.
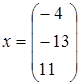4.3.3 Прямые методы. Вычисление определителя методом Гаусса.
Преобразования, выполняемые при прямом ходе алгоритма решения СЛАУ методом Гаусса, позволяют преобразовать матрицу 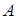системы к треугольному виду. При этом определитель матрицы не изменяется. Для результирующей треугольной матицы определитель равен произведению диагональных элементов:
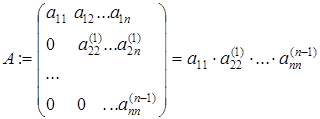. (4.6)
Модификация алгоритма для вычисления лишь определителя матрицы сводится к отбрасыванию строк 6 – 8 псевдокода листинга 4.1, удалению выражения из строки 3, а также к добавлению новой строки 6, в которой находится произведение диагональных элементов. Соответствующий псевдокод будет иметь следующий вид (листинг 4.3):
Листинг 4.3 – Псевдокод вычисления определителя матрицы методом Гаусса
1. для ,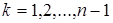
2. для :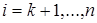
3. ;
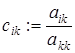4. для :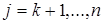
5. .
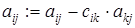6. 
.
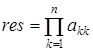4.3.4 Прямые методы. Метод обратной матрицы.
.
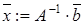4.3.5 Прямые методы. LU-разложение.
LU-разложение есть модификация метода Гаусса.
Пусть матрица коэффициентов при неизвестных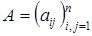 
размером 
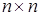является заданной. Для нее необходимо найти верхнюю и нижнюю треугольные матрицы 
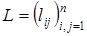и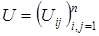 
, соответственно: 
:
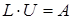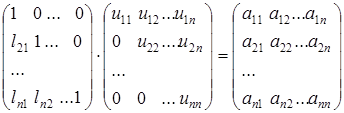. (4.7)
Если равенство (4.7) справедливо, то матричное представление СЛАУ вида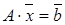 
можно представить эквивалентным выражением
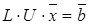. (4.8)
Путем ввода вектора вспомогательных переменных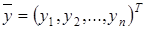 
выражение (4.8) может быть преобразовано к системе 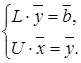(4.9):
(4.9)
Решение системы (4.9) сводится к последовательному решению 2-х систем с треугольными матрицами коэффициентов при неизвестных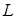 
и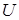 
.
Первый шаг алгоритма – вычисление элементов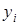 
вспомогательного вектора 
.
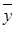Для этого запишем уравнение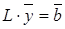 
в развернутом виде:
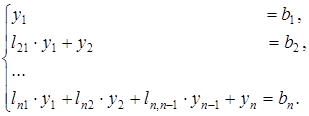(4.10)
Из выражения (4.10) видно, что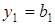 
.
Элементы 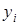вектора 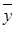для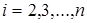 
последовательно вычисляются по формуле
.
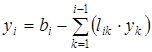После вычисления всех элементов вспомогательного вектора 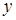развернем вторую систему 
:
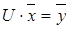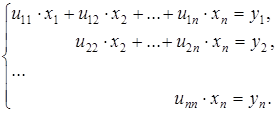(4.11)
На основе системы (4.11) элементы 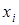вектора неизвестных 
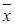находятся в обратном порядке:
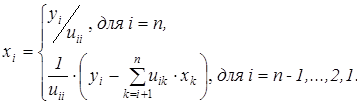
Рассмотрим алгоритм решения СЛАУ методом LU-разложения на примере:
– пусть имеем матрицу ;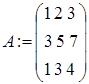
– алгоритм следующий:
1) создадим треугольные матрицы 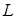и :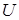
, 
.
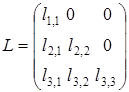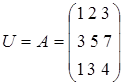Особенности LU-разложения матрицы:
– легко вычислить определитель матрицы:
;
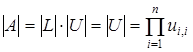– единожды выполнив LU-разложение матрицы А, имеем возможность асимптотически быстрее решать СЛАУ для новых векторов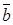 
;
– вычислительная асимптотическая сложность алгоритма решения СЛАУ методом LU-разложения составляет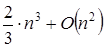 
;
– для последующих решений системы с уже вычисленным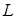и и 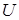матрицами асимптотика составляет 
.
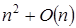Литература:
1. Прасолов В.В. Задачи и теоремы линейной алгебры / В.В. Прасолов. – [2-е изд.]. – М, 2008. – 536 с.
2. Хомицкий Д.В. Сборник задач по линейной алгебре: практикум / Д.В. Хомицкий, А.С. Гаревский, А.В. Тележников. – Нижний Новгород: ННГУ им. Н.И. Лобачевского, 2010. – 51 с.
3. Habgood K. Revisiting Cramer's rule for solving dense linear systems / K. Habgood, I. Arel // Proc. 2010 Spring Simulation Multiconference (USA, FL, Orlando, April 11 – 15, 2010).
4. Реализация численных методов в системе MathCAD. Решение уравнений: метод. указания к выполнению лабораторной работы / составитель Н.Н. Цыбина; под ред. Б.М. Суховилова. – Челябинск: Издательский центр ЮУрГУ, 2011. – 8 с.
5. Вержбицкий В.М. Основы численных методов: учебник для вузов / В.М. Вержбицкий. – М.: Высш. шк., 2002. – 840 с.
6. Муха В.С. Вычислительные методы и компьютерная алгебра: учебно-метод. пособие / В.С. Муха. – Мн.: БГУИР, 2006. – 127 с.
7. Метод Гаусса решения системы линейных уравнений [Электронный ресурс]. – Режим доступа: http://e-maxx.ru/algo/linear_systems_gauss. – Заголовок с экрана.
8. Решение СЛАУ методом JU-разложения [Электронный ресурс]. – Режим доступа: http://habrahabr.ru/sandbox/35982/. – Заголовок с экрана.