Постановка вариационной задачи расчета

РАСЧЕТ КОМПОЗИТНЫХ ПАНЕЛЕЙ ПРИ ПЛОСКОМ НАПРЯЖЕННОМ СОСТОЯНИИ В ПЕРЕМЕЩЕНИЯХ

Введение

Подкрепленные панели являются часто используемыми несущими элементами силовых конструкций, поэтому научить корректно строить аналитические расчетные модели является основной задачей монографии. Построение общего подхода к решению произвольной задачи часто приводит к необоснованным осложнениям. Панели могут иметь различные граничные условия закрепления, различные способы нагружения в ее плоскости как сосредоточенными, так и распределенными силами. Так как задачи решаются в линейной постановке, то любую сложную проблему можно разложить на простые, решать каждую из них отдельно и затем использовать принцип суперпозиции. Аналитические решения имеют преимущество перед современными разностными методами: позволяют получить прямую аналитическую связь между параметрами. Это преимущество удобно использовать в задачах проектирования, если аналитическое решение достаточно просто, но обладает необходимой степенью точности. Для определения напряженно-деформированного состояния в элементах панели, которое позволит оценить их прочность, используется вариационный метод В.З. Власов. Решение проводится в перемещениях, которые в соответствии с этим методом определяются с учетом условий нагружения и закрепления панелей. Такой подход к решению задач позволяет учесть способ и место приложения сил и определить концентрацию напряжений и области их расположения.

Постановка вариационной задачи расчета

Подкрепленная панель состоит из тонкой многослойной композиционной пластины, подкрепляющих эту пластину продольных и поперечных элементов, работающих на растяжение и изгиб, и узлов крепления. Для такой сложной конструкции можно получить разрешающие уравнения равновесия, используя вариационный подход, который позволяет в расчете объединить элементы в единую конструкцию [2]. Для построения расчетных моделей рассмотрим подкрепленную по контуру панель, показанную на рис.3.1, где приведены оси координат, геометрические параметры и один из способов точечного крепления конструкции. Запишем полную энергию представленной системы 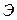в виде суммы потенциальной энергии 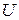и работы внешних сил 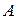в общем виде

.

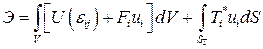Здесь 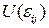- потенциальная энергия рассматриваемой конструкции, выраженная через деформацию 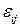; 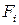- объемные нагрузки; 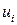- перемещения вдоль рассматриваемых координат; 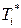- известные поверхностные силы; 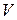- объем рассматриваемого объекта; 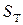- площадь поверхности тела, где действуют известные силы .

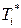Запишем составляющие энергии плоского напряженного состояния панели:

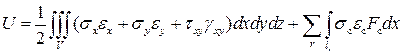; (3.1)

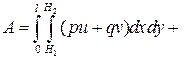
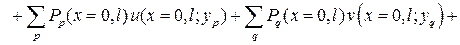
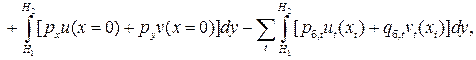(3.2)

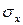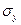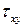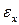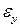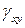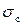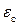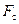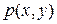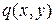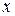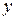где , – средние постоянные по толщине пластины нормальные и касательное напряжения , а , , – соответствующие деформации в панели; , , – напряжение, деформация и площадь поперечных сечений в продольных подкрепляющих элементах панели; и – поверхностные силы в обшивке, параллельные осям и соответственно; 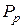и 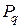– сосредоточенные силы; индексы 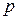и 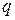– номера сил, прикладываемые в точках с соответствующими координатам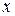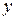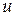и , ; и 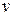– функции перемещений вдоль координат 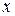и 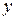соответственно; 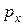и 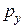– внешние распределенные силы, приложенные на поперечной границе панел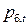и; и 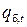– реакции изгиба и удлинения поперечных балок; 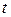– номер балки.

Тогда усилия в пластине будут равны 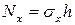; ; 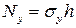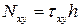, где 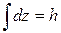– толщина многослойной пластины.

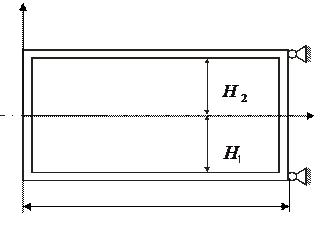
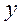
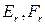
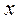
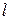
Рис. 3.1. Подкреплённая панель