Реализация матричной формы вычисления перемещений
Вычисление перемещений т. K будем проводить в матричной форме, для чего применим соответствующую формулу Мора:
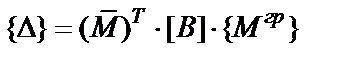 , | (2.5) |
где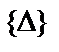 
– матрица-столбец искомых перемещений; 
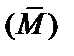– направляющая матрица, каждый столбец которой описывает одну направляющую эпюру, ссылаясь на ординаты контролируемых сечений (символ Т означает операцию транспонирования матрицы); 
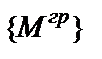– грузовая матрица-столбец, которая описывает грузовую эпюру; 
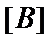– матрица податливости (квадратная), описывающая жесткостные свойства каждого участка расчетной схемы между контролируемыми сечениями.
4.1. Разработка схемы дискретизации.
Формированию матриц предшествует составление схемы дискретизации ЗРС, которая включает нумерацию контролируемых сечений и правило знаков ординат для каждого участка ЗРС (рис. 2.30).
Контролируемые сечения назначаются по данным грузовой эпюры M (рис. 2.11) и направляющих эпюр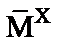 
(рис. 2.21), 
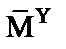(рис. 2.25) и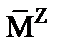 
| Рис. 2.30 |
На рис. 2.30 участки пронумерованы римскими цифрами, а контролируемые сечения – латинскими. Правило знаков принято так, чтобы большинство значений было положительным.
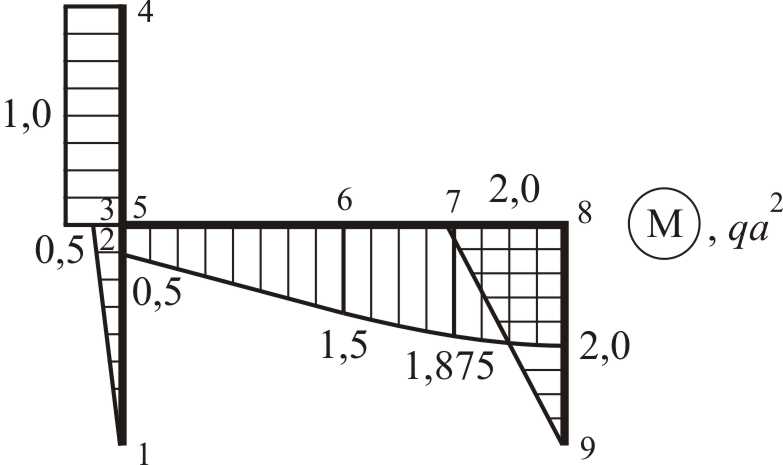
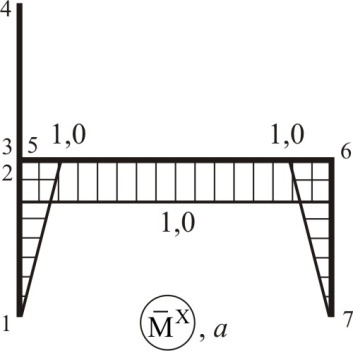
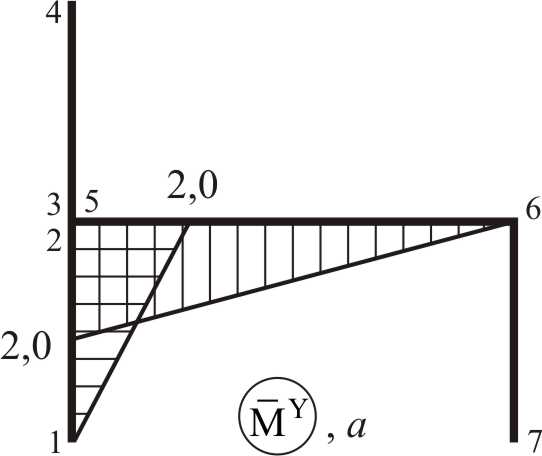
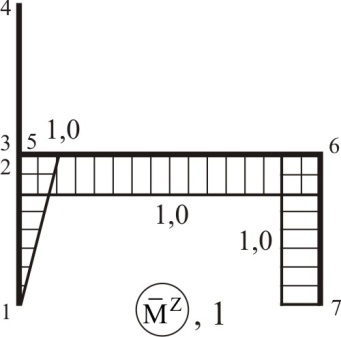
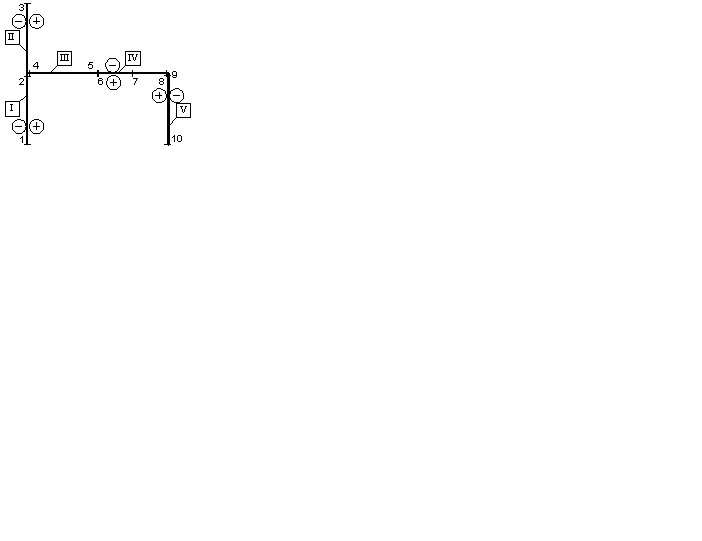
Рис. 2.30
4.2. Матричная форма представления направляющих и грузовой эпюр.
Элементами направляющей матрицы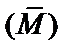 
являются ординаты на направляющих эпюрах изгибающих моментов. Причем первый столбец этой матрицы составляют ординаты, снятые с направляющей эпюры 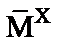(рис. 2.21), второй столбец – ординаты, снятые с направляющей эпюры 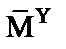(рис. 2.25) и, наконец, третий столбец – ординаты, снятые с направляющей эпюры 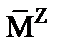(рис. 2.29). Количество строк в матрице соответствует числу контролируемых сечений на схеме дискретизации. Таким образом, размер направляющей матрицы равен 10×3
(10 строк и 3 столбца).
Грузовая матрица формируется по тем же правилам, но ее элементы являются ординатами на грузовой эпюре изгибающих моментов. Размер этой матрицы 10×1.
; 
.
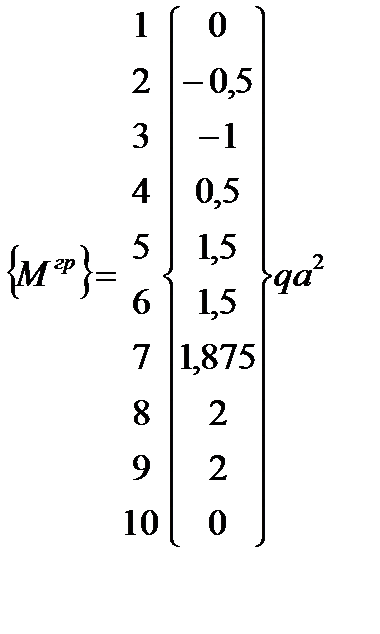4.3. Построение матрицы податливости.
Формирование матрицы податливости 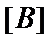осуществляется последовательностью чисто формальных приемов, поскольку для каждого участка на схеме дискретизации вид матрицы является предопределенным.
Формирование матрицы 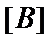включает следующие шаги:
1) Составление матрицы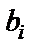 
для участка:
· с законом изменения изгибающего момента M=const по формуле
;
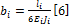· с линейным законом изменения изгибающего момента по формуле
;
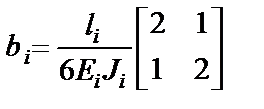· с параболическим законом изменения изгибающего момента по формуле
,
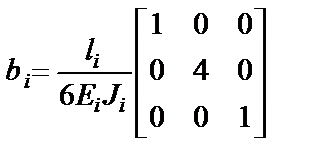где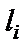 
– длина участка; 
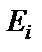– модуль упругости материала (будем считать его одинаковым для всех участков, 
); 
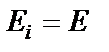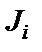– момент инерции сечения.
ü В рассматриваемом примере выполнение этого шага дает следующие выражения для матриц участков:
; 
; 
;
; 
.
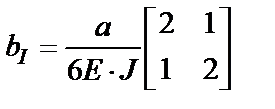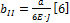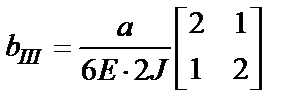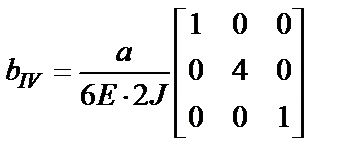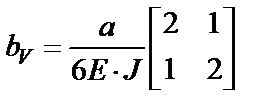2) Определение наибольшего общего знаменателя для всех составленных матриц 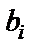и приведение их к этому знаменателю.
ü В данном примере наибольшим общим знаменателем является значение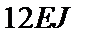 
, соответствующее матрицам 
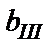и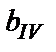 
, составленным для горизонтальных участков ЗРС, на которых момент инерции равен 
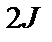(см. рис. 2.5).
Результат приведения всех матриц 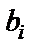к наибольшему общему знаменателю выглядит следующим образом:
; 
; 
;
; 
.
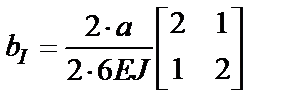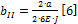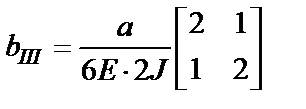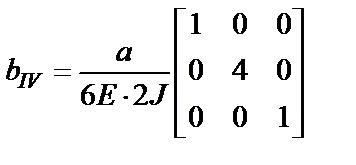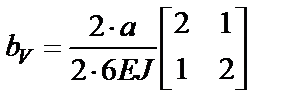3) Внесение коэффициента при а в числителе каждой матрицы 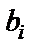под знак матрицы путем перемножения его с каждым элементом стандартной матрицы 
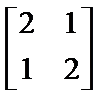– для линейного участка или 
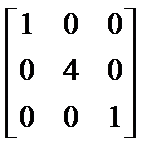– для параболического (эта операция соответствует правилу умножения матрицы на скалярный множитель).
ü В результате выполнения этого шага для задачи примера получаем следующие выражения:
; 
; 
;
; 
.
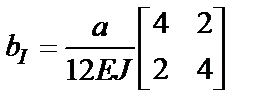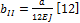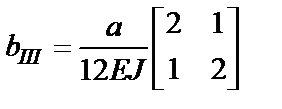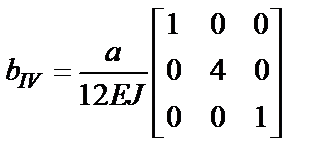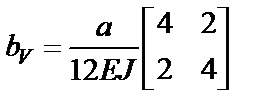Необходимо отметить, что получившиеся в итоге матрицы 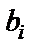имеют общий множитель 
.
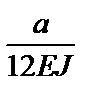4) Составление матрицы податливости .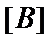
Полученные матрицы 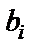по порядку располагают на диагонали матрицы 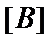, а общий для всех матриц 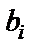множитель является множителем при матрице .
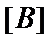ü Выполняя этот шаг, получаем матрицу податливости 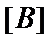размером 10×10. Слева и сверху дана нумерация контролируемых сечений. Отсутствующие элементы матрицы имеют нулевые значения.
4.4. Приемы минимизации размеров матриц.
4.4.1. Способ вычеркивания в матрицах нулевых строк.
Внимательное рассмотрение направляющей 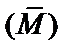и грузовой 
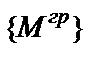матриц показывает, что строка с номером 1 одновременно в обеих матрицах имеет нулевые значения. В таком случае эту строку можно вычеркнуть из сравниваемых матриц, а из матрицы податливости 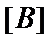вычеркнуть не только строку с этим номером, но и соответствующий столбец. Такая операция позволяет уменьшить размеры матриц до соответственно 10×3, 10×1 и 10×10. В результате получаем:
; 
;
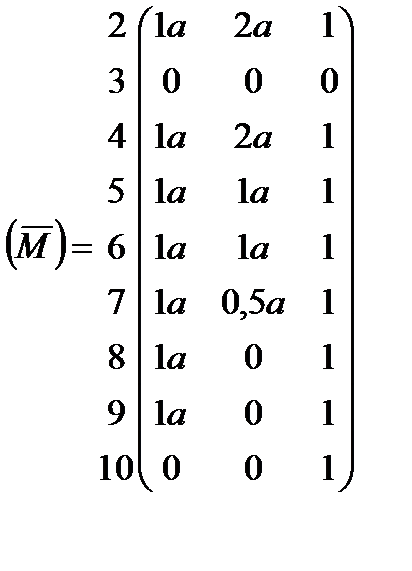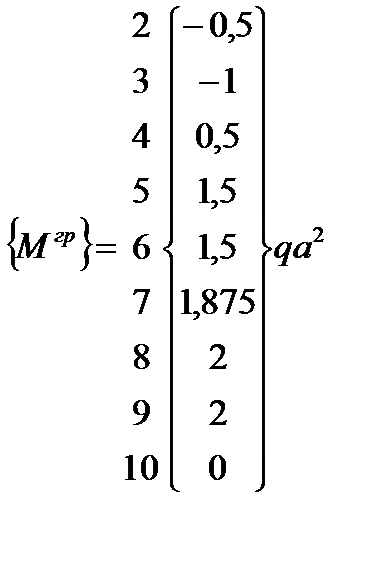4.4.2. Способ вычеркивания в матрицах одной из пары одинаковых строк.
Если продолжать сравнение строк направляющей 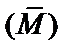и грузовой 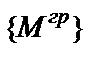матриц, то можно обратить внимание, что в этих матрицах имеются пары строк, состоящие из одинаковых элементов, причем эти строки должны соответствовать смежным сечениям в ЗРС. Такими строками являются пары 5–6 и 8–9. В каждой паре одну из строк (например, строки 6 и 9) можно вычеркнуть из обеих матриц.
Но эти строки (и столбцы) нельзя вычеркивать из матрицы 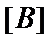! С этой матрицей поступают иначе: цифры, находящиеся на пересечении строк и столбцов с соответствующими номерами складывают, а результат размещают в строке с оставляемым номером (в примере – это 5 и 8), уменьшая тем самым размер и этой матрицы. На стр. 13 овалами выделены те элементы матрицы податливости, которые складываются при выполнении этой операции. Таким образом, минимальные размеры матриц становятся, соответственно 7×3, 7×1 и 7×7.
В результате уменьшения размеров матриц способом вычеркивания одной из пары одинаковых строк получаем:
; 
;
.
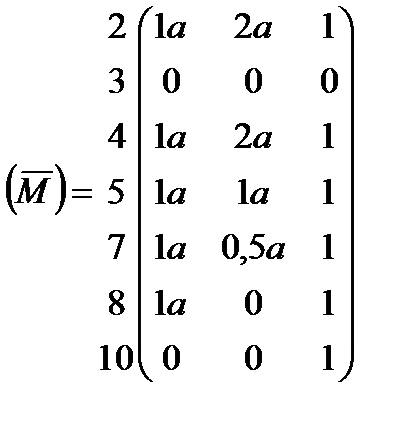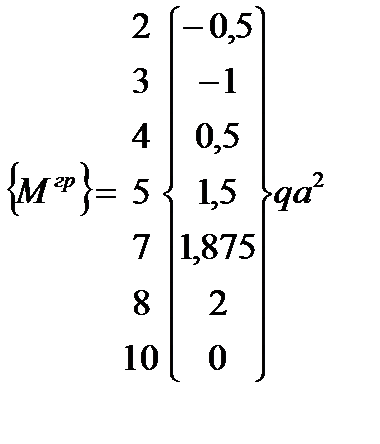4.5. Вычисление искомых перемещений точки K .
Формула (2.5) раскрывает матричную форму для вычисления искомых перемещений т. K. В соответствии с этой формулой для определения перемещений сечения K необходимо выполнить следующие шаги:
1) Записать направляющую матрицу 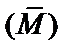в транспонированном виде 
.
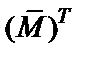Если элементы строк матрицы 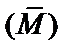расставлены в столбцы, а элементы столбцов расставлены в строки, то полученная матрицаназывается транспонированной к 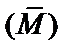и обозначается .
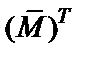2) Умножить транспонированную направляющую матрицу 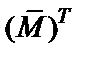на матрицу податливости .
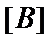3) Умножить полученную в предыдущем пункте матрицу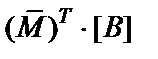 
на грузовую матрицу 
.
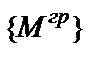4) Записать полученные значения перемещений т. K (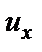 
, 
, 
).
; 
; 
.
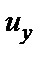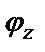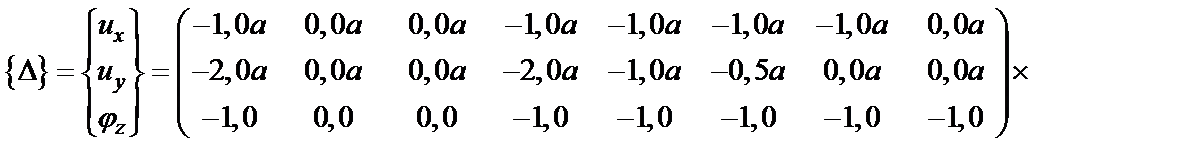
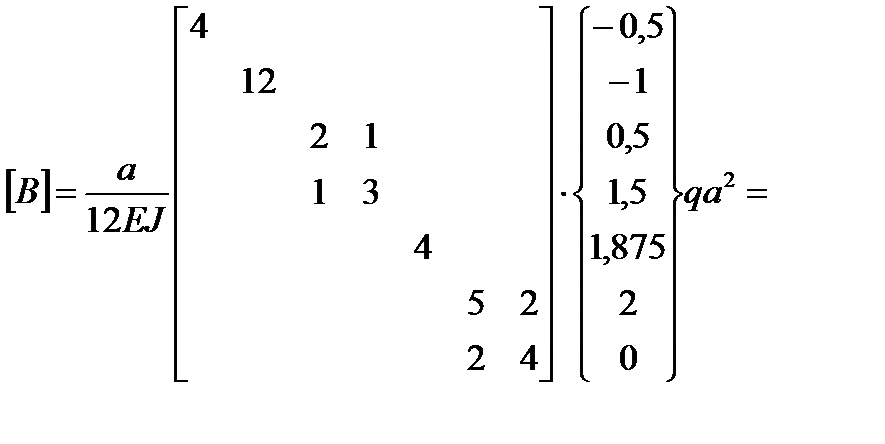
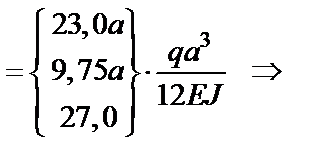
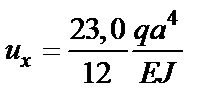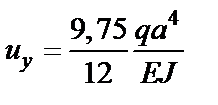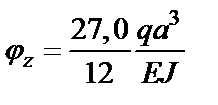1.9167 0.8125 2.25
Здесь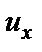 
– перемещение т.K вдоль оси X; 
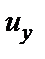– перемещение т.K вдоль оси Y;
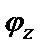– угол поворота т.K относительно оси Z.
Итак, основная задача примера решена – мы располагаем значениями перемещений т. K оси заданной расчетной схемы. Положительные значения полученных перемещений означают то, что, задавая направляющие нагрузки в виде единичных сил, мы «угадали» истинное направление перемещений.