Задачи для решения на занятии. Практическое занятие №1
Практическое занятие №1
Тема: Кинематика и динамика поступательного движения твердого тела.
Цель: обобщение и систематизация знаний, умений по данной теме; формирование практических навыков в решении задач; развитие познавательных возможностей, памяти, трудолюбия.
Краткие теоретические сведения
Таблица 1.1 - Основные законы и формулы
| Физические законы, переменные | Формулы |
Мгновенная скорость: где 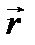 - радиус – вектор материальной точки, t – время; - радиус – вектор материальной точки, t – время; 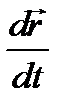 – производная радиус – вектора материальной точки. – производная радиус – вектора материальной точки. 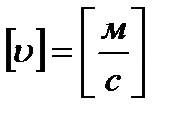 | 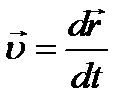 |
| Модуль вектора скорости: где S – путь | 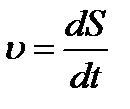 |
| Модуль средней скорости: | 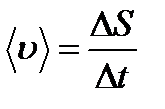 , , 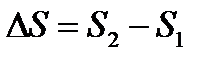 , , 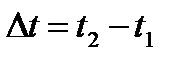 |
Мгновенное ускорение: 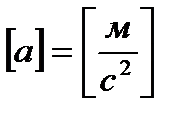 | 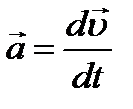 |
| Модуль вектора ускорения при прямолинейном движении: | 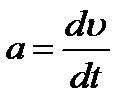 |
| Скорость и путь при движении: 1) равномерном,2) равнопеременном, υ0 – начальная скорость, а>0 при равноускоренном движении, а<0 при равнозамедленном движении. | 1) υ=const, 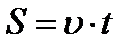 , 2) , 2) 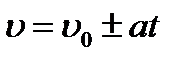 , , 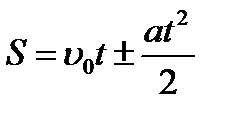 |
Основное уравнение динамики поступательного движения (II закон Ньютона), где 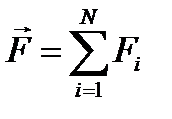 - результирующая сила. - результирующая сила. 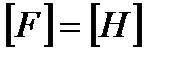 | 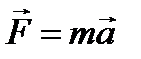 |
| Силы в природе: 1) сила притяжения, закон всемирного тяготения, где G = 6,67·10-11Н·м2/кг2, m1,m2 – массы тел, r- расстояние между ними. | 1) 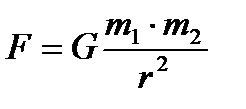 |
| 2) сила тяжести, где g =9,8 м/с2 – ускорение свободного падения, m – масса тела, 3) вес тела, если υ = const, если тело движется с ускорение вверх, если тело движется с ускорение вниз, 4) сила упругости, закон Гука: где k – коэффициент упругости (жесткость), Δх – абсолютное удлинение, 5) сила трения, где μ – коэффициент трения, N – сила реакции опоры. | 2) 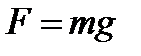 3) 3) 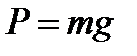 , , 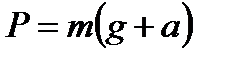 , , 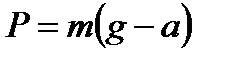 4) 4) 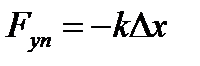 5) 5) 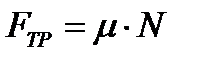 |
Примеры решения задач
1.Первую половину времени своего движения автомобиль двигался со скоростью 80км/ч, а вторую половину времени - со скоростью 60км/ч. Какова средняя скорость движения автомобиля в км/ч?
Дано:
υ1 = 80 км/ч,
υ2 = 60 км/ч,
t1=t2=t/2/
Найти:
υср – ?
Решение
Средняя скорость движения поезда
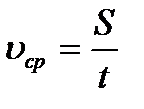 ,
,
где S – путь, t – время движения на всем участке пути.
Длина пути складывается из двух разных участков пути: на первом автомобиль движется со скоростью υ1 и длина участка пути
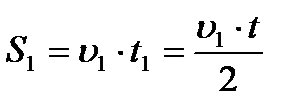 ,
,
на втором автомобиль движется со скоростью υ2 и длина этого участка пути
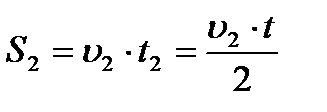 .
.
Тогда весь путь равен:
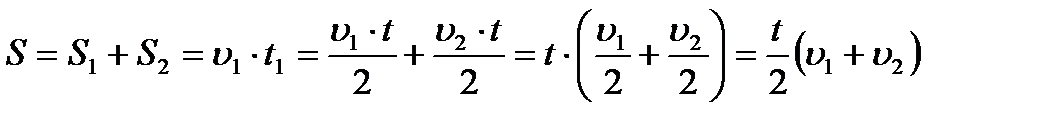 .
.
Найдем среднюю скорость движения:
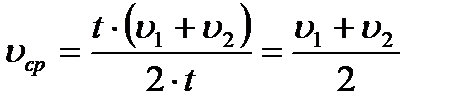 ,
,
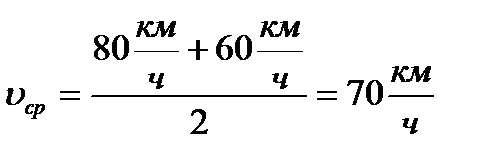 .
.
Ответ: 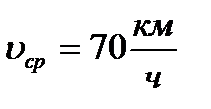 .
.
2.Уравнение движений двух велосипедистов заданы выражениями 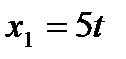 и
и 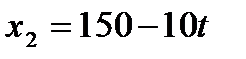 . Построить график
. Построить график 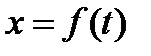 установить время и место их встречи.
установить время и место их встречи.
Дано:
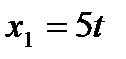
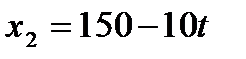
Найти:
х0=?
t0=?
Решение:
Определим время встречи, тогда 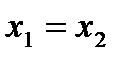
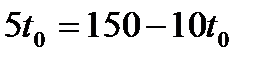
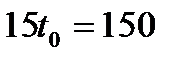
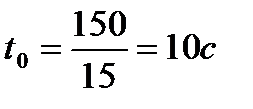
Место встречи
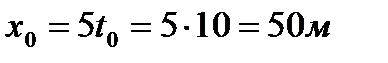
Построим графики движения
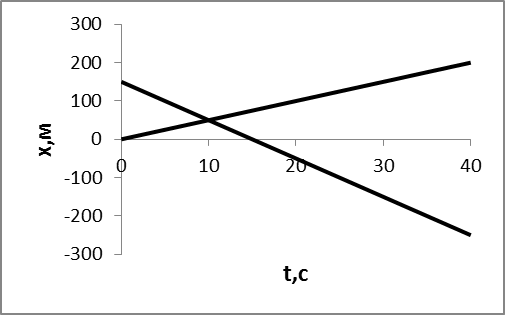
Рисунок 1.1
Ответ: 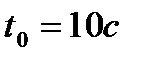 ,
, 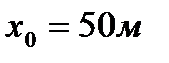
3.Вагон движется равнозамедленно с ускорением -0,5 м/с2. Начальная скорость вагона 54 км/ч. Через сколько времени вагон остановится и какой путь пройдет до остановки?
Дано:
а = -0,5 м/с2,
υ0 = 54 км/ч = 15 м/с,
υ=0.
Найти:
t– ?
S– ?
Решение
Скорость при равноускоренном движении описывается выражением:
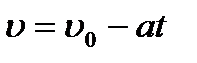 ,
,
так как υ = 0, по условию, то
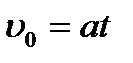 ,
,
отсюда
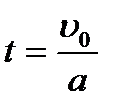
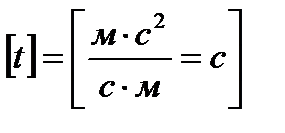 ,
,
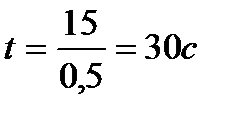
Путь при равнозамедленном движении вычисляется по формуле:
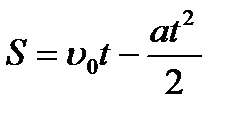 ,
,
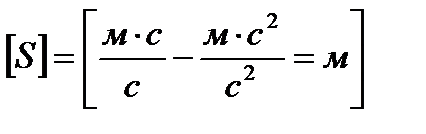 ,
,
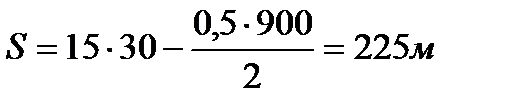 .
.
Ответ: 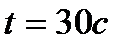 ,
, 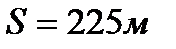 .
.
4.Лыжник спускается с горы длиной 100 м. Начальная скорость 10 м/с, ускорение 0,5 м/с2. Сколько времени длился спуск?
Дано:
S = 100 м,
υ0 = 10 м/с,
a = 0,5 м/с2.
Найти:
t– ?
Решение
Лыжник движется равноускорено. Перемещение лыжника можно определяется по формуле:
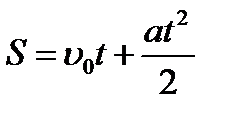 .
.
По условию задачи S = 100 м, υ0 = 10 м/с, a = 0,5 м/с2, тогда
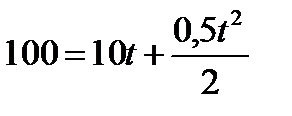 ,
,
или,
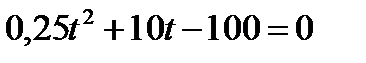
Решим квадратичное уравнение.
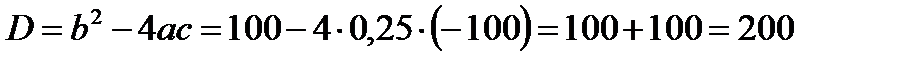
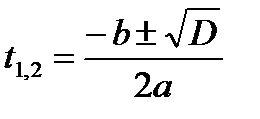 ,
,
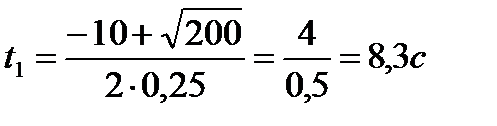 ,
,
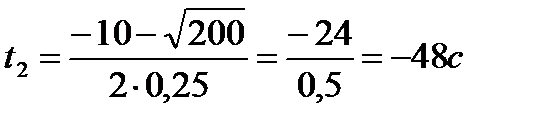 (не удовлетворяет условию задачи)
(не удовлетворяет условию задачи)
Ответ: 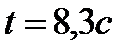
5.Зависимость пройденного телом прямолинейного пути от времени задается уравнением 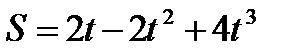 , м. Найти скорость и ускорение тела через 5 с после начала движения.
, м. Найти скорость и ускорение тела через 5 с после начала движения.
Дано:
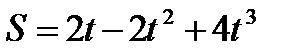 , м,
, м,
t = 5 c.
Найти:
υ – ?
а – ?
Решение
Скорость, первая производная от перемещения ко времени
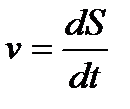 ,
,
тогда
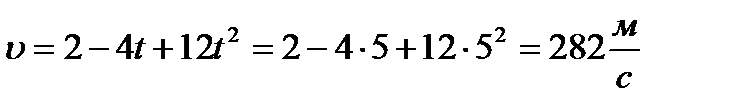
Ускорение, первая производная от скорости материальной точки, тогда
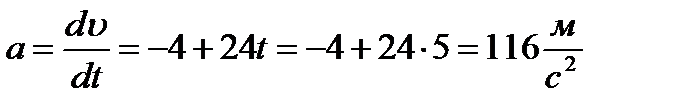 .
.
Ответ: 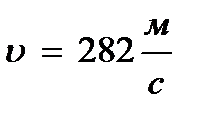 ,
, 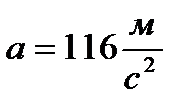 .
.
6.Автомобиль массой 1 т трогается с места и через 20 с достигает скорости 30 м/с. Найти силу тяги, если коэффициент сопротивления равен 0,05.
Дано:
m=1 т=103 кг,
t=20 c,
υ = 30 м/с,
υ0 = 0,
μ = 0,05.
Найти:
Fтяг - ?
Решение
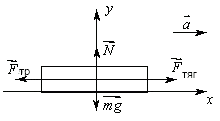
Рисунок 1.2
На автомобиль действуют четыре силы: сила тяжести 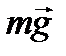 , сила реакции опоры
, сила реакции опоры 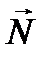 , сила тяги двигателя
, сила тяги двигателя 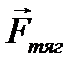 и сила трения
и сила трения 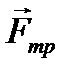 .За положительное направление оси х примем направление движения автомобиля, а ось у направим вертикально вверх. Так как движение равноускоренное, то вектор ускорения направлен в сторону движения и совпадает с направлением оси х. Для решения задачи воспользуемся вторым законом Ньютона и определением силы трения скольжения.
.За положительное направление оси х примем направление движения автомобиля, а ось у направим вертикально вверх. Так как движение равноускоренное, то вектор ускорения направлен в сторону движения и совпадает с направлением оси х. Для решения задачи воспользуемся вторым законом Ньютона и определением силы трения скольжения.
По второму закону Ньютона
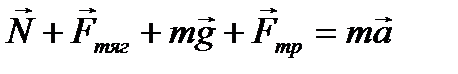 .
.
В проекциях на оси
ОХ: 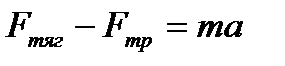 ,
,
ОУ: 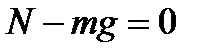 ,
,
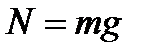
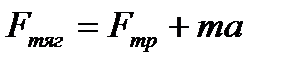
По определению 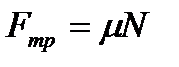 , так как
, так как 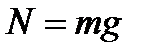 , то
, то 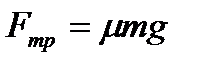 , тогда
, тогда
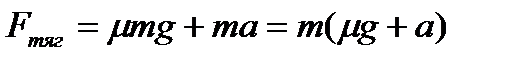 .
.
Ускорение тела
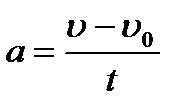 ,
,
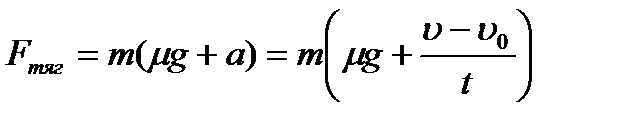 ,
,
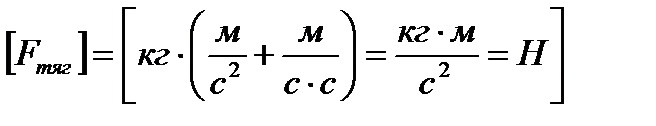 ,
,
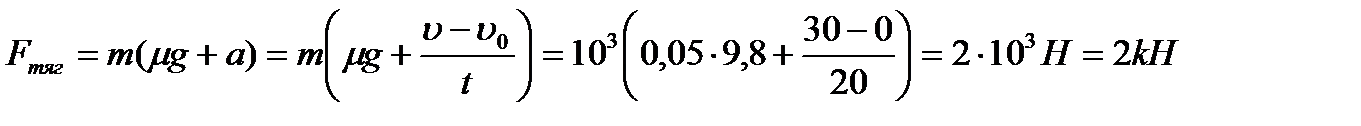
Ответ: Fтяг=2кН.
7. Через блок перекинута нить, на концах которой подвешены грузы общей массой 10 кг. После освобождения грузы приходят в движение с ускорением 1 м/с2 . Найти массу каждого груза.
Дано:
m1 +m2 =10 кг,
a = 1 м/с2.
Найти:
m1 – ?
m2 – ?
Решение
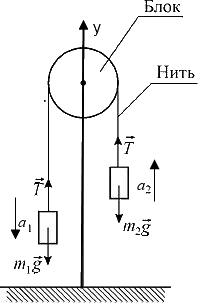
Рисунок 1.3
Предположим, что нить и блок невесомы и нет трения в оси блока. Тогда силы, действующие на грузы 1 и 2 со стороны нити, равны между собой (рис.) Из нерастяжимости нити следует равенство по модулю ускорений грузов 1 и 2. Запишем уравнение движение грузов. По второму закону Ньютона для каждого тела в проекции на вертикалью ось ОУ:
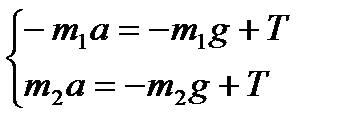 (1)
(1)
Из системы (1) получим
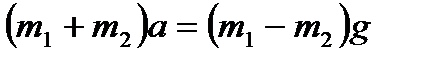 ,
,
так как 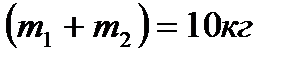 , то
, то
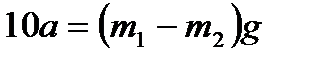 ,
,
отсюда
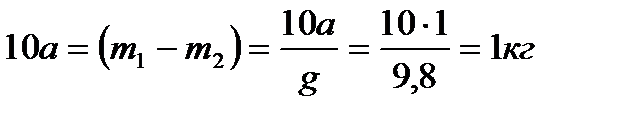 .
.
Таким образом
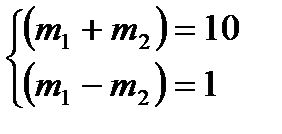 ,
,
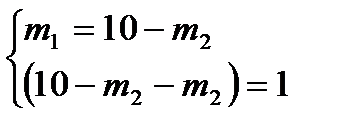 ,
,
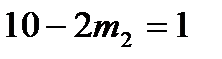 ,
,
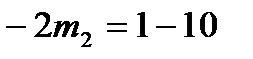 ,
,
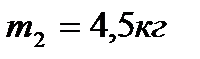 ,
,
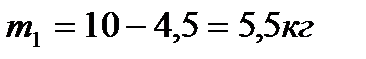
Ответ: 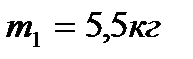
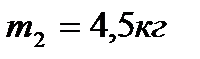 .
.
8. Два медных шарика ( с плотностями ρ = 8,6·103кг/м3) с диаметрами D1 =4 см и D2 = 6 см находятся в соприкосновении друг с другом. Найти силу гравитационного взаимодействия этой системы.
Дано:
ρ = 8,6·103кг/м3,
D1 =4 см = 0,04 м,
D2 = 6 см = 0,06 м
Найти:
F – ?
Решение
Из закона всемирного тяготения, сила притяжения шаров
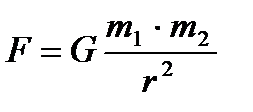 , (1)
, (1)
где G гравитационная постоянная, r – расстояние между центрами шаров, m1 и m2 - массы шариков
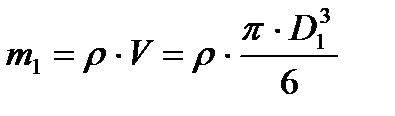 , (2)
, (2)
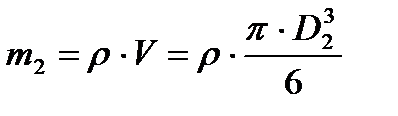 (3)
(3)
Расстояние между центрами шаров
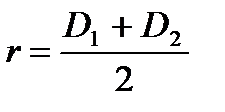 (4)
(4)
Подставляя (2-4) в (1) получим:
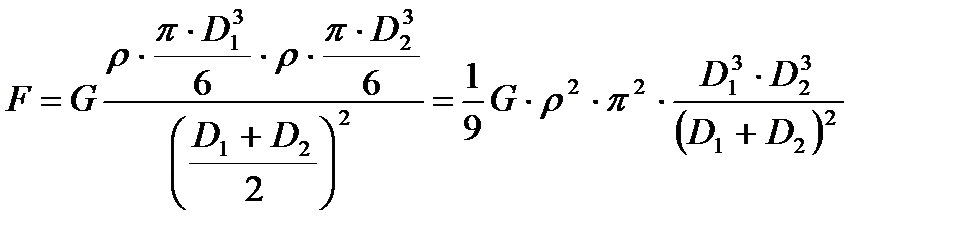 ,
,
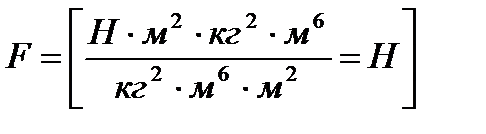 ,
,
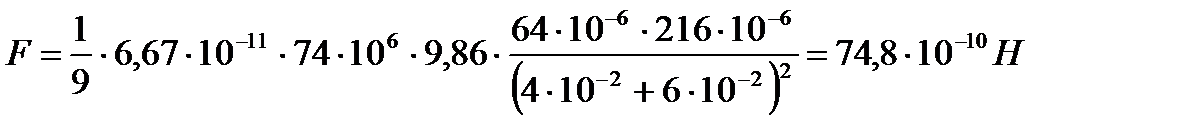 .
.
Ответ: 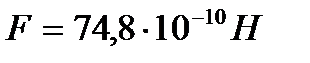
9.Студент подвесил на недеформированную вертикально расположенную пружину груз массой 300 г. Пружина удлинилась на 4 см. Какой массы груз следует добавить к первому грузу, чтобы удлинение пружины стало равным 6 см?
Дано:
m1 = 300 г = 0,3 кг,
Δx1 = 4 см = 0,04м,
Δx2 = 6 см = 0,06 м.
Найти:
Δm– ?
Решение
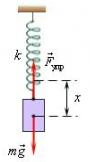
Рисунок 1.4
На груз, подвешенный на пружине, действуют силы: сила тяжести 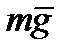 , направленная вниз, сила упругости
, направленная вниз, сила упругости 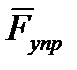 , направленная вверх.
, направленная вверх.
По закону Гука сила упругости
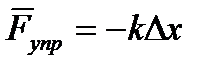 , (1)
, (1)
где k – жесткость пружины, Δх – удлинение. (знак «минус» говорит о том, что 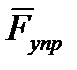 – возвращающая сила).
– возвращающая сила).
Так как груз находится в равновесии, то 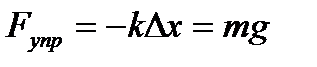 , отсюда коэффициент жесткости для груза:
, отсюда коэффициент жесткости для груза:
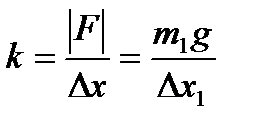 , (2)
, (2)
после добавления груза, массу обозначим m2, жесткость же пружины не изменилась, т.е
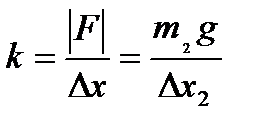 . (3)
. (3)
Приравнивая (2) и (3) получим:
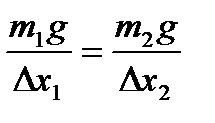 ,
,
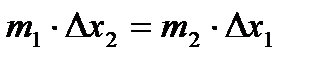 ,
,
отсюда
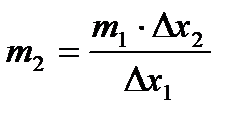 ,
,
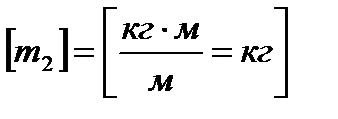 ,
,
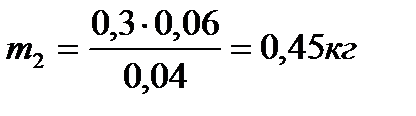 .
.
Таким образом, чтобы удлинение пружины стало равным 6 см, следует добавить, к первому грузу массу Δm
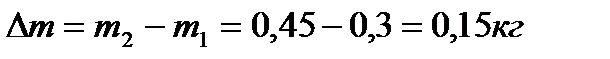 .
.
Ответ: 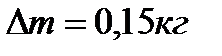 .
.
10.Камень массой 1,05 кг, скользящий по поверхности льда со скоростью 2,44 м/с, под действием силы трения останавливается через 10 с. Найти силу трения, считая ее постоянной.
Дано:
m = 1,05 кг,
υ0 = 2,44 м/с,
υ =0,
t = 10 с.
Найти:
Fтр– ?
Решение
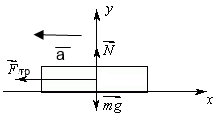
Рисунок 1.5
На камень действуют силы: сила тяжести 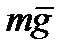 , направленная вниз, сила реакции опоры
, направленная вниз, сила реакции опоры 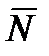 , направленная вверх, сила трения
, направленная вверх, сила трения 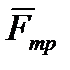 , направленная противоположно движению. По второму закону Ньютона
, направленная противоположно движению. По второму закону Ньютона
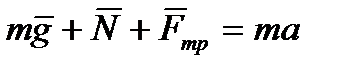 ,
,
в проекции на оси:
ОХ: 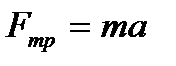 , (1)
, (1)
Ускорение тела
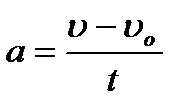 ,
,
так как υ =0, то
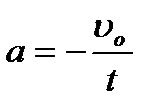 ,
,
тогда
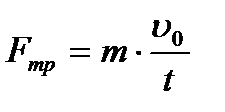 ,
,
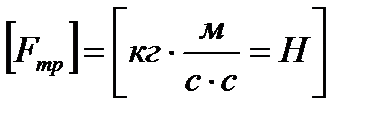 ,
,
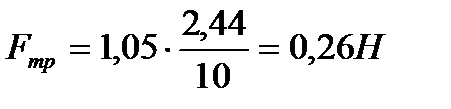
Ответ: 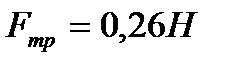 .
.
Задачи для решения на занятии
1.По графику зависимости скорости движения тела от времени определить характер движения тела, начальную скорость и ускорение на каждом участке
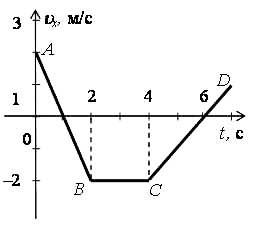
Рисунок 1.6
2.Найти место и время встречи двух тел 2 способами (графически и аналитически). (Ответ: t = 5 c, х = 45 м)
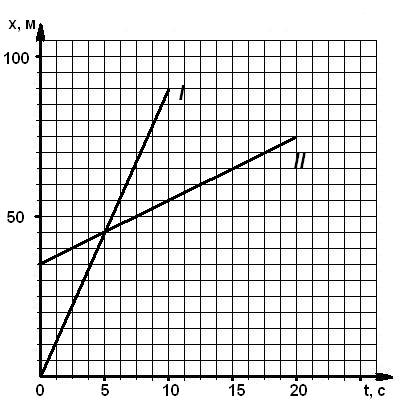
Рисунок 1.7
3.Зависимость пройденного телом пути от времени задается уравнением 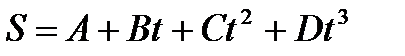 , где А =1 м, В = 1,5 м/с, С = 0,1 м/с2, D = 0,03 м/с3. Определить путь, пройденный телом за 10 с и скорость в этот момент времени. (Ответ: S = 56 м, υ = 12,5 м/с)
, где А =1 м, В = 1,5 м/с, С = 0,1 м/с2, D = 0,03 м/с3. Определить путь, пройденный телом за 10 с и скорость в этот момент времени. (Ответ: S = 56 м, υ = 12,5 м/с)
4. Движение двух тел описывается уравнением 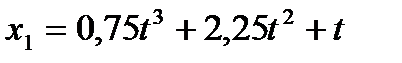 ,
, 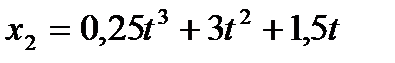 . Определить величину скоростей этих тел и момент времени, когда ускорения их будут одинаковы, а также значение ускорения в этот момент времени. (Ответ: υ1 = 3,81 м/с, υ2 = 4,69 м/с, а = 6,75 м/с2)
. Определить величину скоростей этих тел и момент времени, когда ускорения их будут одинаковы, а также значение ускорения в этот момент времени. (Ответ: υ1 = 3,81 м/с, υ2 = 4,69 м/с, а = 6,75 м/с2)
5. Под действием силы F=10 Н тело движется прямолинейно так, что зависимость пройденного телом пути от времени задается уравнением 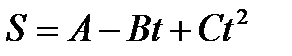 , где С=1 м/с2. Найти массу m тела. (Ответ: m = 5 кг)
, где С=1 м/с2. Найти массу m тела. (Ответ: m = 5 кг)
6.Тело движется вниз равноускоренно по наклонной плоскости, и зависимость пройденного пути от времени задается уравнением 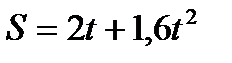 . Найти коэффициент трения μ тела о плоскость, если угол наклона плоскости к горизонту равен 300.(Ответ: μ = 0,2)
. Найти коэффициент трения μ тела о плоскость, если угол наклона плоскости к горизонту равен 300.(Ответ: μ = 0,2)
7.К нити подвешен груз массой m = 500 г. Определите силу натяжения нити, если нить с грузом: 1) поднимать с ускорением 2 м/с2; 2) опускать с ускорением 2 м/с2. (Ответ: 1) Т=5,9 Н; 2) Т = 3,9 Н).
8.По графику зависимости проекции силы упругости от удлинения (рис.1.8) найдите жесткость резинового шнура.(Ответ: k≈300 Н/м)
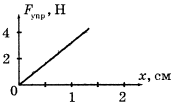
Рисунок 1.8.
9.Невесомый блок укреплен в вершине наклонной плоскости, составляющей с горизонтом угол α = 300. Гири 1 и 2 одинаковой массы m1 = m2 =1 кг соединены нитью и перекинуты через блок найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гири о наклонную плоскость и трением в блоке пренебречь.(Ответ: а=2,45 м/с2; Т= 7,35 Н)
10. Тело массой m = 2 кг падает в воздухе с ускорением а=9,3 м/с2. Определите силу сопротивления FС воздуха. (Ответ: FС =1Н).
Вопросы для самоконтроля
1. Дайте определения кинематических характеристик поступательного движения (перемещение, траектория, путь, скорость, ускорение).
2. Какое прямолинейное движение называют равноускоренным, равнозамедленным?
3. Чем отличаются понятия средних и мгновенных скоростей и ускорений?
4. Дайте определения динамических характеристик поступательного движения (сила, масса, импульс).
5. Какова задача динамики? Сформулируйте три закона Ньютона. В каких системах отсчета они справедливы?
6. Сформулируйте закон всемирного тяготения.
7. В чем заключается физический смысл гравитационной постоянной.
8. Дайте определение веса тела.
9. Какое состояние тела называют невесомостью?
10. Куда направлена сила трения скольжения и чему она равна?
11. Какие силы называют силами упругости?
12. Сформулируйте закон Гука.
