По переходной характеристике (кривой разгона)

Под параметрической идентификацией ОР понимают определение его математической модели по результатам экспериментальных исследований. При параметрической идентификации оператор модели полагают известным и задача сводится к определению параметров модели.

Для идентификации объекта регулирования – лабораторной ЭП, температура в которой контролируется датчиком ТПУ0304/М2 (см. рис. 4.2), используем инженерные методики определения параметров модели ОР по экспериментально полученной кривой разгона. Изменение температуры в ЭП может быть описано дифференциальным уравнением второго порядка, а в качестве модели ЭП может быть выбрано типовое динамическое звено 2-го порядка (апериодическое) с запаздыванием

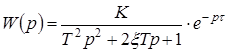. (4.1)

Для идентификации апериодического звена второго порядка метод Ормана есть наилучшим, поскольку он не требует определения точки перегиба на кривой разгона, которое возможно осуществить лишь приблизительно.

Тогда для идентификации ОР нужно определить четыре параметра: коэффициент передачи К, постоянную времени Т, коэффициент демпфирования ξ и время запаздывания τ.

Для построения математической модели объекта регулирования использовался метод восстановления параметров модели по эмпирическим данным. Для этого на лабораторной установке была получена экспериментальная кривая разгона процесса нагрева печи (рис. 4.3).

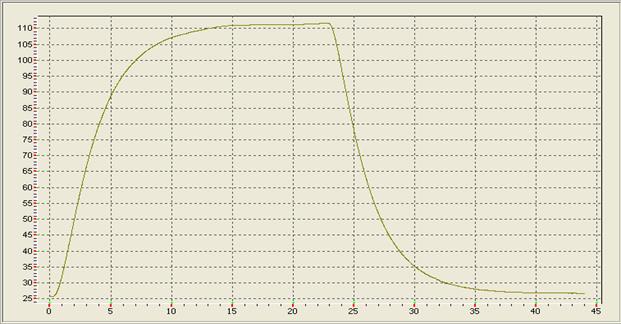
Рис. 4.3. Экспериментальная кривая разгона ЭП

Коэффициент передачи ОР равен отношению установившегося значения выхода к входному воздействию

.

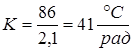Чистое запаздывание определяется временем, на протяжении которого после поступления входного сигнала, последний продолжает быть равным нулю. Таким образом, время запаздывания t = 20 с.

Для определения параметров Т и ξ рассматриваем переходной процесс без запаздывания, то есть принимаем за начало отсчета времени момент t₀ = τ = 20с.

При проведении исследований удобнее использовать график, начинающийся с нуля. Поэтому сместим ось ординат на величину, равную температуре окружающей среды (температуре в лаборатории кафедры АПП) Т_лаб = 26°С.

По кривой переходного процесса определяем момент времени t₇, в который

h (t₇) = 0,7h(∞) = 0,7×86 = 60,2°С,

при этом t₇ =265 с.

Далее находим t₃ =(t₇/3) и определяем h(t₃):

t₃ = 265/3 = 88 с,

h(t₃) =19°С.

Нормированное значение выхода h_н(t₃) при t = t₃ равно

h_н(t₃) = h(t₃)/К = 24/86 = 0,22.

Определяем коэффициент демпфирования ξ в зависимости от h_н(t₃) по табл. 4.1.

Таблица 4.1

Зависимость коэффициента демпфирования ξ от нормированного значения переходной характеристики h_н(t₃)

hн(t3)	ξ	hн(t3)	ξ	hн(t3)	ξ
0,196	1,0	0,263	1,5	0,298	2,0
0,212	1,1	0,273	1,6	0,302	2,1
0,227	1,2	0,280	1,7	0,306	2,2
0,241	1,3	0,287	1,8	0,308	2,3
0,263	1,4	0,293	1,9	0,310	2,4

С учетом линейной интерполяции, коэффициент демпфирования составит ξ = 1,15.

Постоянную времени Т определяем из соотношения

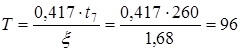с. (4.2)

В результате искомая передаточная функции с учетом запаздывания и действительного коэффициента передачи имеет вид

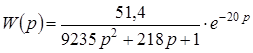. (4.3)

Рекомендуется использовать для аппроксимации (4.3) функцию передачи

Т,°С

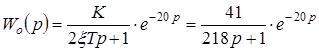. (4.4)

t, c

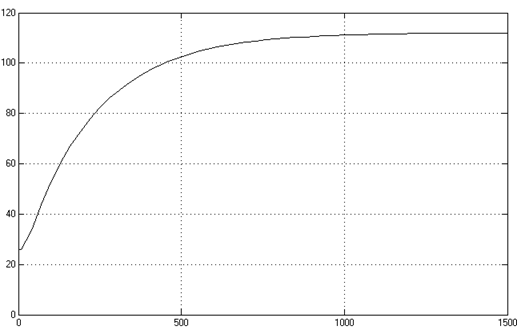
Рис. 4.4. Переходный процесс модели ЭП с учетом запаздывания и действительного коэффициента передачи

Сопоставим экспериментальную кривую с кривой искомой передаточной функции и вычислим ошибку идентификации, применив интегральный критерий

. (4.5)

Интегральная ошибка составила 0,25°С или 0,1% от максимального значения температуры, что подтверждает правильность идентификации параметров объекта регулирования.