Математическое и линейное программирование

Буравлева О.Ю.

Математические методы в коммерческой деятельности: Учеб.-метод. пособие.

Часть 1/О.Ю.Буравлева. Тамбов: Изд-во Тамб.гос. техн. ун-та, 2005. с.

Рассмотрены теоретические и практические вопросы раздела «Математическое и линейное программирование» в курсе «Математика в экономике».

Предназначено студентам специальности 080301 «Коммерция (торговое дело)» в качестве дополнительной литературы для самостоятельной работы при изучении курса «Математика в экономике».

УДК 330.83(07)

ББК У.в 611я73

© Буравлева О.Ю., 2005

© Тамбовский государственный

технический университет (ТГТУ), 2005

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ

1. МАТЕМАТИЧЕСКОЕ И ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ…………………5

2. СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ…………………………………………………………………..11

2.1 Нахождение начального опорного решения и переход к новому опорному решению………………………………………………………………………………………. 12

2.2 Преобразование целевой функции при переходе от одного опорного решения к другому……………………………………………………………………………………….. 14

2.3 Улучшение опорного решения………………………………………………………. 15

2.4 Алгоритм симплексного метода……………………………………………………... 16

3.МЕТОД ИСКУССТВЕННОГО БАЗИСА…………………………………………….....20

3.1 Особенности алгоритма метода искусственного базиса……………………………..22

4.ТЕОРИЯ ДВОЙСТВЕННОСТИ………………………………………………………….26

4.1 Виды математических моделей двойственных задач………………………………...26

4.2 Общие правила составления двойственных задач……………………………………28

5.ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ КАК ЧАСТНЫЙ СЛУЧАЙ ОБЩЕЙ РАСПРЕДЕЛИТЕЛЬНОЙ ЗАДАЧИ………………...31

5.1 Общая характеристика распределительной задачи………………………………….. 31

5.2 Транспортная задача…………………………………………………………………….32

5.3 Транспортная задача с ограничениями на пропускную способность……………….47

5.4 Транспортная задача по критерию времени…………………………………………. 52

ЛИТЕРАТУРА…………………………………………………………………………………55

ВВЕДЕНИЕ

Дисциплина «Математика в экономике» является региональной составляющей блока естественнонаучных дисциплин Государственного образовательного стандарта второго поколения подготовки специалистов коммерции по специальности 080301 – Коммерция (торговое дело).

Данное учебно-методическое пособие посвящено разделу «Математического и линейного программирования». В нем рассмотрены теоретические вопросы и на конкретных примерах показаны возможности использования математического и линейного программирования как инструмента для решения задач коммерции.

Пособие будет полезным для студентов при самостоятельной работе над конкретными заданиями по курсу «Математика в экономике».

МАТЕМАТИЧЕСКОЕ И ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ.

Математическое программирование – это раздел высшей математики, посвященный решению задач, связанных с нахождением экстремумов функций нескольких переменных при наличии ограничений на переменные. Методами математического программирования решаются задачи о распределении ресурсов, планировании выпуска продукции, ценообразовании, транспортные задачи и т.п.

Построение математической модели экономической задачи включает следующие этапы: 1) выбор переменных задачи; 2) составление системы ограничений; 3) выбор целевой функции.

Переменными задачиназываются величины 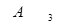, которые полностью характеризуют экономический процесс. Их обычно записывают в виде вектора A=( ).

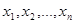Система ограниченийвключает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий.

Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи, и экстремум которой требуется найти.

Общая задача математического программирования формулируется следующим образом: найти экстремум целевой функции

Z (X)= +

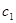
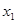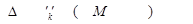
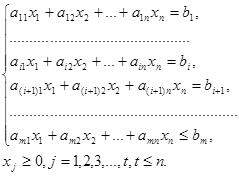
Данная запись означает следующее: найти экстремум целевой функции задачи и соответствующие ему переменные при условии, что эти переменные удовлетворяют системе ограничений и условиям неотрицательности.

Допустимым решением (планом) задачи линейного программирования называется любой n-мерный вектор X,удовлетворяющий системе ограничений и условиям неотрицательности.

Множество допустимых решений (планов) задачи образует область допустимых решений (ОДР).

Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение (план) задачи, при котором целевая функция достигает экстремума.

В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися. В том случае, когда все ограничения – уравнения, и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической. Она может быть представлена в координатной, векторной и матричной формах записи.

Рассмотрим математические модели простейших экономических задач: задача о диете и задача о составлении плана производства.

Задача о диете.

Задача о диете возникает при составлении наиболее экономного (т.е. наиболее дешевого) рациона питания животных, удовлетворяющего определенным медицинским требованиям.

Предположим, что в нашем распоряжении имеется n продуктов питания (сено, зерно, комбикорм, соль и т.д.). Обозначим эти продукты через 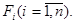Предположим, что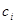 есть стоимость единицы веса (например, стоимость одного килограмма) продукта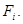

Рациональная диета должна доставлять животному определенные компоненты (белки, жиры, углеводы, витамины, микроэлементы и т.д.). Обозначим эти компоненты через 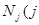= 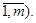Тогда можно составить таблицу – справочник, указывающую, какое количество каждого компонента имеется в единице веса каждого продукта (табл. 1.1.).

Таблица 1.1.

	F	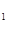F	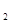…	F	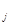…	F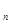
N	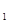a	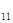a	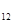…	a	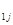…	a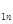
N	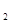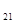a	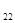a	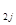…	a	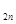…	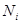a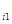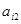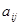
…	…	…	…	…	…	…
	a		…		…	a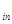
…	…	…	…	…	…	…
N	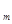a	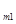a	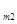…	a	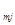…	a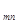

Таким образом, величина 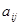есть количество i-го компонента, содержащегося в единице веса j-го продукта. Матрица A= 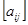называется матрицей питательности.

Рацион кормления должен указать, какое количество x i-го продукта должно быть скормлено животному за определенный срок (скажем, за месяц). Он означает, что за этот срок животное должно получить единиц первого 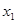продукта, единиц второго, 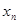единиц n-го продукта.

Что же требуется от рациона? Во-первых, должны быть выполнены определенные медицинские требования, которые заключаются в том, что за указанный срок животное должно получить не менее определенного количества каждого компонента (не менее определенного количества белков, жиров, витаминов и т.д.). Обозначим через b 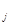то минимальное количество j-го компонента, которое должно получить животное. Тогда рацион кормления должен удовлетворять ограничениям:

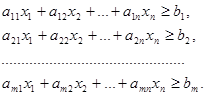(1.1)

Кроме того, очевидно, что все переменные 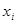неотрицательны, т.е.

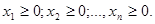(1.2)

Пусть стоимость единицы веса i-го продукта равна 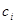.Тогда весь наш рацион будет стоить:

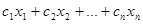(1.3)

Мы, естественно, хотели бы понести минимальные затраты на содержание животных. Поэтому задача приобретает вид: найти рацион минимальной стоимости при выполнении медицинских ограничений (1.1) и естественных ограничений (1.2). Математически это выглядит так:

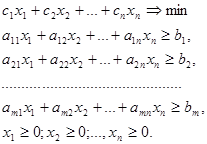(1.4)

Обратите внимание на полученный результат. Во-первых, достаточно реальная задача приобрела строгую математическую форму. Во-вторых, целевая функция (стоимость рациона) является линейной функцией переменных 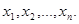В третьих, сами ограничения на значения переменных 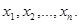имеют вид линейных неравенств. Все это и определило название этого класса задач – задачи линейного программирования.

Рассмотрим теперь другую классическую задачу.

Задача о составлении плана производства.

Рассмотрим деятельность некоторой производственной единицы (цеха, отдела и т.д.). пусть наша производственная единица может производить некоторые товары .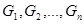

Для производства этих товаров приходится использовать некоторые сырьевые ресурсы. Пусть число этих ресурсов есть m; обозначим их через .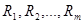

Технологией производства товара 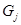назовем набор чисел 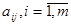, показывающий, какое количество i-го ресурса необходимо для производства единицы товара 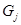. Это можно записать в виде технологической матрицы, которая полностью описывает технологические потребности производства и элементами которой являются числа 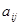(табл.1.2.).

Таблица 1.2.

			…		…
			…		…
			…		…
…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…
			…		…

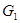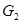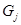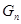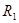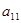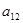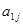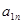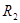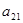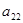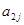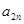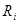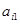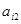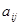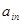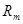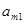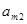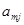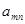При наличии 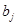запасов каждого ресурса мы планируем произвести 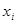единиц i-го товара. При этом нет возможности превысить пределы имеющихся у нас ресурсов и наш план производства 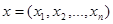должен удовлетворять ограничениям:

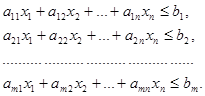
(1.5)
при очевидных условиях неотрицательности переменных :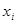

.

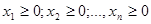Естественно, мы стремимся получить за нашу продукцию возможно больше. Поэтому стоящая перед нами задача составления плана производства приобретает вид:

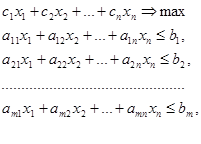(1.6)

.

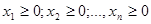Вновь получается линейная целевая функцияи ограничения имеют характер линейных неравенств. Таким образом, мы снова имеем дело с задачей линейного программирования.

Не будем рассматривать примеры других задач линейного программирования. Отметим лишь, что они встречаются очень часто при оптимизации самых разнообразных производственных и экономических задач.

Задача линейного программирования может быть решена графически. Алгоритм решения для случая двух переменных имеет вид:

1. Строится область допустимых решений.

2. Строится вектор нормали с точкой приложения в начале координат.

3. Перпендикулярно вектору проводится одна из линий уровня, например, линия уровня, проходящая через начало координат.

4. Линия уровня перемещается до положения опорной прямой. На этой прямой и будет находится максимум или минимум функции.

В зависимости от вида ОДР и целевой функции Z(X) задача может иметь единственное решение, бесконечное множество решений или не иметь ни одного оптимального решения.

Графическим методом можно решать также задачи линейного программирования, имеющие каноническую форму и удовлетворяющую условию n-r 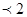, где n – число неизвестных системы, r – ранг системы векторов условий (число линейно независимых уравнений системы).

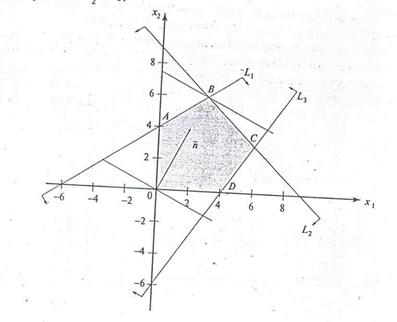
Пример. Решить задачу линейного программирования графическим методом:

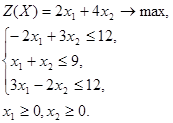
Р е ш е н и е. Изобразим на плоскости систему координат 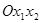и покажем граничные прямые области допустимых решений (номера прямых соответствуют их порядковому номеру в системе).

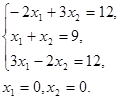
Область допустимых решений определяется многоугольником OABCD (рис. 1.1).

Для линий уровня 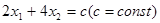строим нормальный вектор 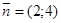. Перпендикулярно вектору 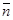построим одну из линий уровня (на рис. 1.1 она проходит через начало координат). Так как задача на максимум, то перемещаем линию уровня в направлении вектора 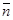до опорной прямой. В данном случае опорной прямой является прямая, проходящая через точку пересечения граничных прямых 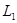и 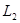, т.е. через точку B= 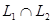. Для определения координат точки B решаем систему уравнений:

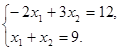
Получаем 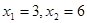. Это и будет оптимальное решение данной задачи, которому соответствует максимальное значение целевой функции max Z(X) = 2 * 3 + 4 * 6 = 30.