Элементы теории множеств
ВАРИАНТ 3
Задача 1. Докажите методом математической индукции, что при любом натуральном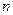 
имеет место равенство
.
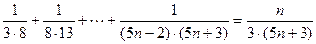Задача 2. Докажите методом математической индукции, что при любом натуральном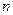 
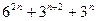делится на 33.
Задача 3. У профессора есть три любимых каверзных вопроса. В группе 20 студентов. Профессор решил задавать каждому из студентов по одному каверзному вопросу. Сколько есть возможностей провести опрос в группе?
Задача 4. Найдите коэффициент при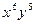 
в разложении 
.
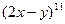Задача 5. Даны числовые множества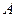 
и 
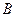. Найдите 
, 
, 
, 
, 
, 
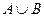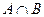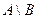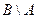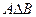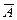и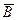 
. Изобразите 
.
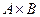а)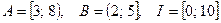 
,
б)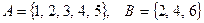 
, где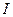 
— множество цифр 
.
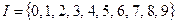Задача 6. Каждый из 54 членов Клуба Любителей Овчарок владеет немецкими, кавказскими или азиатскими овчарками. 20 владеют немецкими, 23 — кавказскими и 23 азиатскими, 4 имеют немецких и азиатских овчарок,5 — немецких и кавказских, 6 — азиатских и кавказских. У скольких членов клуба есть собаки всех трех пород? Сколько членов клуба имеют только одну породу собак?
Задача 7. Проверьте, является ли заданное отношение рефлексивным, антирефлексивным, симметричным, антисимметричным, транзитивным, эквивалентным, отношением порядка.
Отношение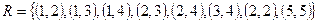 
на множестве 
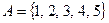. Запишите матрицу отношения 
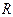и постройте граф.
Задача 8. На множестве действительных чисел задана операция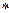 
по формуле 
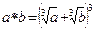. Проверьте, является ли она коммутативной, ассоциативной.
Задача 9. Установите взаимно однозначное соответствие между числовыми промежуткам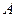и и 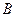аналитически, если 
.
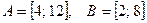ИДЗ №1 ПО ДИСКРЕТНОЙ МАТЕМАТИКЕ
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
ВАРИАНТ 4
Задача 1. Докажите методом математической индукции, что при любом натуральном 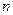имеет место равенство
.
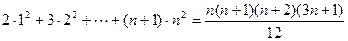Задача 2. Докажите методом математической индукции, что при любом натуральном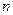 
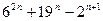делится на 17.
Задача 3. Позывные американских радиостанций состоят из трех или четырех букв и начинаются с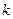 
или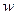 
. Сколько может существовать различных позывных (в английском языке 26 букв)?
Задача 4. Найдите коэффициент при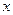 
в разложении 
.
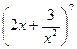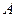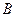Задача 5. Даны числовые множества и . Найдите 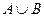, , 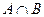, , 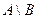, 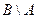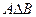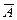и 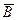. Изобразите .
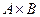а)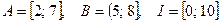 
,
б)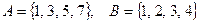 
, где 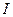— множество цифр .
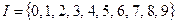Задача 6. 70 первокурсников потока АВ – 08 в качестве домашнего задания придумывали задачу на пересечение трех множеств. К помощи Интернета прибегли 25 человек, к помощи сокурсника 30 человек, самостоятельно сочиняли 47 человек. Один студент часть задачи взял с Интернета, часть списал у сокурсника, часть додумал сам, 13 человек часть взяли с Интернета, а часть додумали сами, 8 человек часть взяли с Интернета, а часть списали у сокурсника, 15 человек часть списали у сокурсника, а часть придумали сами. Сколько человек были полностью самостоятельными? Сколько человек не сделали домашнего задания?
Задача 7. Проверьте, является ли заданное отношение рефлексивным, антирефлексивным, симметричным, антисимметричным, транзитивным, эквивалентным, отношением порядка.
Отношение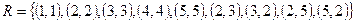 
на множестве 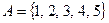. Запишите матрицу отношения 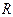и постройте граф.
Задача 8. На множестве действительных чисел задана операция 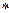по формуле 
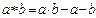. Проверьте, является ли она коммутативной, ассоциативной.
Задача 9. Установите взаимно однозначное соответствие между числовыми промежуткам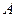и и 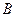аналитически, если 
.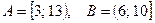