Критическая область. Область принятия гипотезы. Критические точки

После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества, одно из которых содержит значения критерия, при которых нулевая гипотеза отвергается, а другое – при которых она принимается.

Критической областьюназывают совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы(областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.

Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если области принятия гипотезы – гипотезу принимают.

Так как критерий K – одномерная случайная величина, то все ее возможные значения принадлежат некоторому интервалу и, соответственно, должны существовать точки, разделяющие критическую область и область принятия гипотезы. Такие точки называются критическими точками.

Различают одностороннюю (правостороннюю и левостороннюю) и двустороннюю критические области.

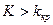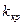Правостороннейназывают критическую область, определяемую неравенством , где – положительное число.

Левостороннейназывают критическую область, определяемую неравенством 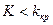, где 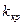– отрицательное число.

Двусторонней называют критическую область, определяемую неравенствами 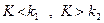, где 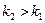. В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется неравенствами 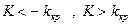или равносильным неравенством 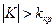. Различия между вариантами критических областей иллюстрирует следующий рисунок.

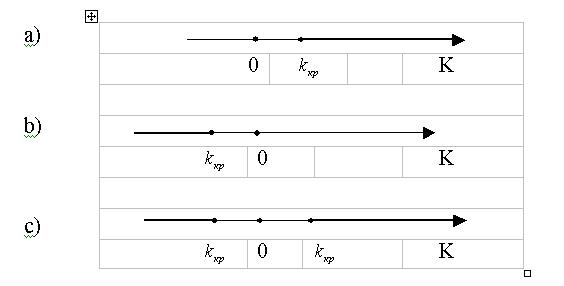
Рис. 1. Различные варианты критических областей a) правосторонняя, b) левосторонняя, с) двусторонняя

Резюмируя, сформулируем этапы проверки статистической гипотезы:

· Формулируется нулевая гипотеза ;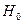

· Определяется критерий K, по значениям которого можно будет принять или отвергнуть 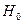и выбирается уровень значимости ;

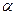· По уровню значимости определяется критическая область;

· По выборке вычисляется значение критерия K, определяется, принадлежит ли оно критической области и на основании этого принимается 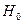или .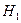

Проверка гипотезы о равенстве математических ожиданий двух нормальных случайных величин при известной дисперсии.

Обозначим через п и т объемы больших (n > 30, т > 30) неза-висимых_выборок, по которым найдены соответствующие выборочные средние х и у. Генеральные дисперсии D (X) и D (Y) известны.

Правило 1. Для того чтобы при заданном уровне значимости 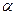проверить нулевую гипотезу Н_о: М (Х) = М(У) о равенстве матема­тических ожиданий (генеральных средних) двух нормальных гене­ральных совокупностей с известными дисперсиями (в случае больших выборок) при конкурирующей гипотезе Н₁: М (X) 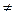М (Y), надо вычислить наблюдаемое значение критерия

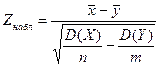
и по таблице функции Лапласа найти критическую точку 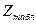из равенства

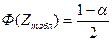
Если | Z_набл | < Z_табл — нулевая гипотеза принимается. Если | Z_набл | >Z_табл —нулевую гипотезу отвергают.

Правило2. При конкурирующей гипотезе Н₁ :М(Х)>М(У) находят критическую точку 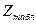по таблице функции Лапласа из равенства

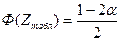
Если | Z_набл | < Z_табл — нулевая гипотеза принимается. Если | Z_набл | >Z_табл —нулевую гипотезу отвергают.

Правило3. При конкурирующей гипотезе Н₁ :М (X) < М (У) находят «вспомогательную точку» 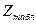по правилу 2. Если | Z_набл | < Z_табл — нулевая гипотеза принимается. Если | Z_набл | >Z_табл — нулевую гипотезу отвергают.

Пример: По двум независимым выборкам, объемы которых п = 40 и т = 50, извлеченным из нормальных генеральных совокупностей, найдены выборочные средние: х=130 и y=140. Генеральные дисперсии известны: D(X) = 80, D(Y)= 100. Требуется при уровне значимости 0,01 прове­рить нулевую гипотезу Н_о: М (X) = М (У) при конкури­рующей гипотезе H₁: М(Х) 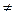М(У).

Решение.Найдем наблюдаемое аначение критерия:

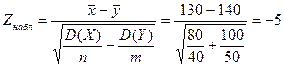
По условию, конкурирующая гипотеза имеет вид М(Х) 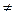М(У), поэтому критическая область—двусторонняя.

Найдем правую критическую точку из равенства

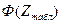=(1 —а)/2=(1 —0,01 )/2=0,495.

По таблице функции Лапласа находим

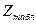=2,58.

Так как| Z_набл | >Z_табл, то в соответствии с правилом 1 нулевую гипотезу отвергаем. Другими словами, выбороч­ные средние различаются значимо.