Нелинейные преобразования сигналов и ФУ
Нелинейные преобразователи сигналов описываются нелинейными дифференциальными уравнениями (в том числе нулевого порядка для резистивных цепей), у которых хотя бы один коэффициент зависит от их решения (искомой функции). Соответственно, их схема содержит хотя бы один
       Спектр Спектр 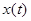  0 wс w Спектр 0 wс w Спектр 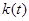  0 W w Спектр 0 W w Спектр 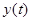 0 W wс–W wс wс+W w Рис.3.3. Спектры 0 W wс–W wс wс+W w Рис.3.3. Спектры 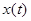 , , 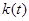 и и 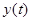 |
нелинейный элемент, параметр(ы) которого зависит от протекающего тока или приложенного напряжения.
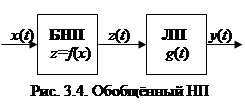


 Анализ нелинейных ФУ в общем случае является сложной задачей, которая существенно упрощается, если возможно разделить ФУ на две независимые части, сосредоточив всю нелинейность в безынерционном нелинейном преобразователе (БНП) а всю инерционность – в линейном (ЛП), как это показано на рис. 3.4. Назовём такую структуру обобщённым нелинейным преобразователем (ОНП). Для анализа ОНП достаточно по известной функциональной характеристике БНП
Анализ нелинейных ФУ в общем случае является сложной задачей, которая существенно упрощается, если возможно разделить ФУ на две независимые части, сосредоточив всю нелинейность в безынерционном нелинейном преобразователе (БНП) а всю инерционность – в линейном (ЛП), как это показано на рис. 3.4. Назовём такую структуру обобщённым нелинейным преобразователем (ОНП). Для анализа ОНП достаточно по известной функциональной характеристике БНП 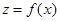 (для безынерционной цепи это обычная функция, а не оператор) определить его реакцию
(для безынерционной цепи это обычная функция, а не оператор) определить его реакцию 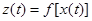 на заданное воздействие
на заданное воздействие 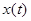 , а затем проанализировать прохождение
, а затем проанализировать прохождение 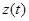 через ЛП одним из вышеуказанных методов.
через ЛП одним из вышеуказанных методов.
Рассмотрим возможности изменения спектра сигнала при его прохождении через БНП – цепь 0-го порядка. Для таких цепей в теории широко используют два основных метода спектрального анализа реакции в зависимости от вида аппроксимации функциональной характеристики БНП:
1) метод кратных дуг – при полиномиальной аппроксимации
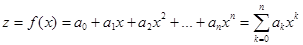 ,
,
2) метод угла отсечки (коэффициентов Берга) – при кусочно-линейной аппроксимации.
Чтобы воспользоваться первым методом, достаточно помнить тригонометрическую формулу
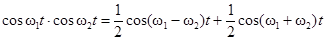
и её частный случай (при 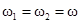 )
)
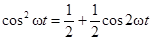 .
.
Результаты анализа спектрального состава реакции БНП с полиномиальной функциональной характеристикой при моно- и бигармоническом воздействии приведены в таблице 3.1. В ней указаны только частоты спектральных составляющих реакции.
Из этой таблицы следует, что БНП обогащает спектр воздействия постоянной составляющей, кратными гармониками и колебаниями комбинационных частот вида 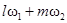 , где
, где 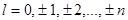 ,
, 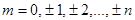 , причём порядок комбинационных частот
, причём порядок комбинационных частот 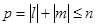 (не превосходит степени n полинома, аппроксимирующего функциональную характеристику БНП). Этот вывод можно распространить и на случай полигармонического воздействия.
(не превосходит степени n полинома, аппроксимирующего функциональную характеристику БНП). Этот вывод можно распространить и на случай полигармонического воздействия.
Выводы
1. Нелинейные ФУ обогащают спектр воздействия новыми спектральными компонентами.
2. Новые спектральные компоненты реакции нелинейных ФУ являются гармониками частот воздействия или колебаниями комбинационных частот вида
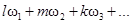 , где l,m,k=0, ±1, ±2,…
, где l,m,k=0, ±1, ±2,…
Таблица 3.1
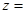 | Спектральный состав 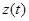 при при | |
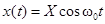 | 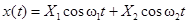 | |
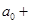 | ||
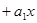 | w0 | 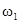 , , 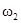 |
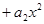 | 0, 2w0 | 0, 2w1, 2w2, 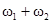 , , 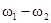 |
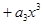 | 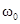 , 3w0 , 3w0 | 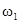 , , 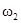 , , 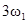 , , 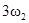 , , 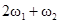 , , 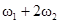 , , 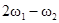 , , 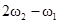 |
| + … | ||
+ 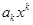 | 0, 2w0, 4w0,…, kw0 при k = 2q, 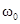 , 3w0,…, kw0 при k = 2q+1, q = 1, 2, 3,… , 3w0,…, kw0 при k = 2q+1, q = 1, 2, 3,… | 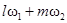 ; ; 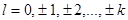 , , 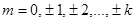 , , 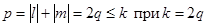 , , 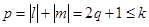 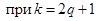 , q = 1, 2, 3,… , q = 1, 2, 3,… |
| + … | ||
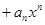 | 0, 2w0, 4w0,…, nw0 при n = 2q, 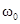 , 3w0,…, nw0 при n = 2q+1, q = 1, 2, 3,… , 3w0,…, nw0 при n = 2q+1, q = 1, 2, 3,… | 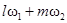 ; ; 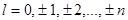 , , 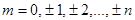 , , 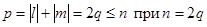 , , 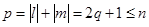 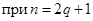 q = 1, 2, 3,… q = 1, 2, 3,… |
Контрольные вопросы
1. Сформулируйте задачи анализа и синтеза ФУ.
2. Дайте классификацию ФУ по виду описывающих их дифференциальных уравнений.
3. Каковы принципиальные ограничения на возможности преобразования сигналов в линейных ФУ?
4. Что можно использовать в качестве функциональных характеристик линейных ФУ?
5. Какие типовые ФУ, используемые в системах связи, можно реализовать в классе линейных цепей?
6. Каковы возможности параметрических ФУ по преобразованию сигналов?
7. Опишите характер обогащения спектров сигналов в параметрических ФУ.
8. Каковы возможности нелинейных ФУ по преобразованию сигналов?
9. Какие виды аппроксимации функциональных характеристик безынерционных нелинейных преобразователей целесообразны в режимах а) слабого сигнала, б) сильного сигнала?
 | Рис. 3.5. Исследование преобразований сигналов в линейных ФУ |
10. Какой метод спектрального анализа реакции нелинейного ФУ используют при аппроксимации его функциональной характеристики степенным полиномом ?
11. Какой метод спектрального анализа реакции нелинейного ФУ используют при кусочно-линейной аппроксимации его функциональной характеристики?
12. Опишите спектральный состав реакции нелинейного ФУ на моногармоническое воздействие.
13. Опишите спектральный состав реакции нелинейного ФУ на полигармоническое воздействие.
14. Нарисуйте схему перемножителя сигналов и укажите назначение её элементов.
15. При каких условиях кольцевой диодный перемножитель обеспечивает «чистое» перемножение сигналов?
16. В чём сущность метода фазовой компенсации побочных продуктов нелинейного преобразования сигналов?
