Предполные классы двоичных функций
Определение:
Предполным классом К называется неполный класс, при добавлении любой функции 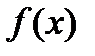 , которая не принадлежит ему, получается класс полный.
, которая не принадлежит ему, получается класс полный.
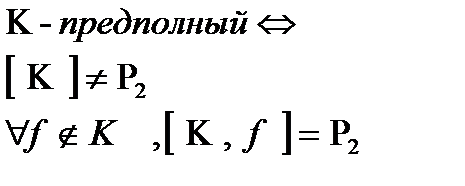
Утверждение:
Предполный класс является замкнутым.
Доказательство: Допустим противное, что некоторый предполный класс К не замкнут: 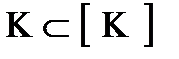 , тогда рассмотрим функцию
, тогда рассмотрим функцию
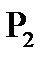 |
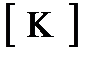 f f |
т.е. [ K,f ] не полный
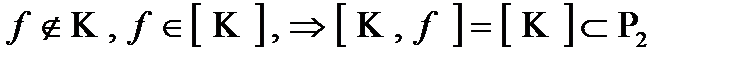
Теорема:
В классе булевых функций 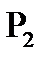 есть ровно пять предполных классов :
есть ровно пять предполных классов : 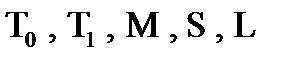 .
.
Доказательство:
В начале покажем, что данные классы являются предполными, а затем покажем, что других предполных классов нет.
1) Рассмотрим 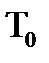 .
.
Данный класс содержит функции:
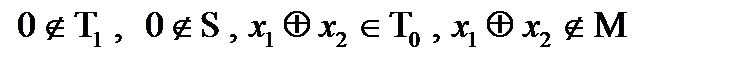
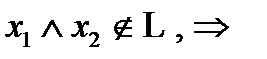 поэтому класс Т0 не принадлехит классам Т1, S, М, L.
поэтому класс Т0 не принадлехит классам Т1, S, М, L.
Рассмотрим произвольную 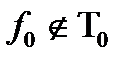 , тогда
, тогда 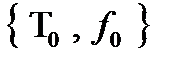 не принадлежит ни одному из пяти классов Поста, следовательно по теореме Поста является полной, следовательно класс
не принадлежит ни одному из пяти классов Поста, следовательно по теореме Поста является полной, следовательно класс 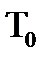 является предполным.
является предполным.
2) Рассмотрим Т1:
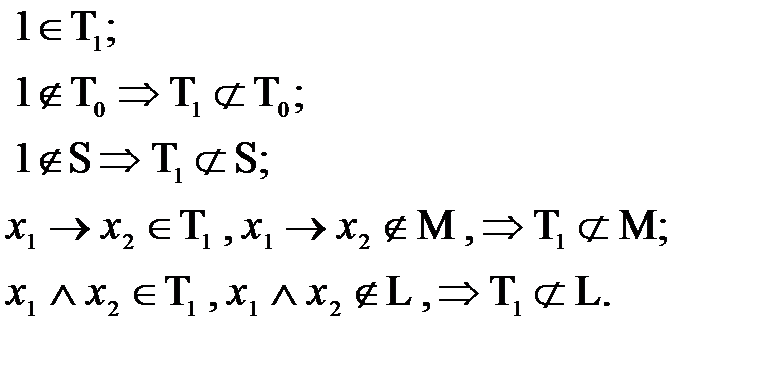
Рассмотрим произвольную 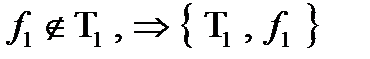 не принадлежит ни одному из пяти классов, следовательно по теореме Поста является полной, следовательно
не принадлежит ни одному из пяти классов, следовательно по теореме Поста является полной, следовательно 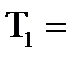 предполный.
предполный.
3) Рассмотрим S:
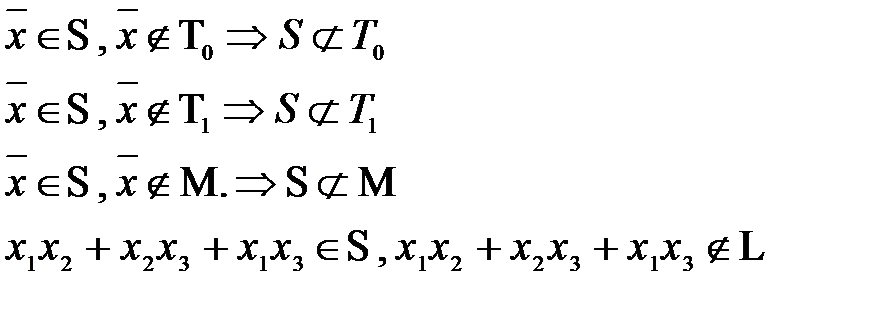
Рассмотрим 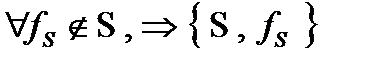 не принадлежит ни одному из пяти классов Поста, следовательно по теореме Поста является полной, следовательно
не принадлежит ни одному из пяти классов Поста, следовательно по теореме Поста является полной, следовательно 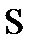 предполный .
предполный .
4) Рассмотрим 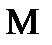 :
:
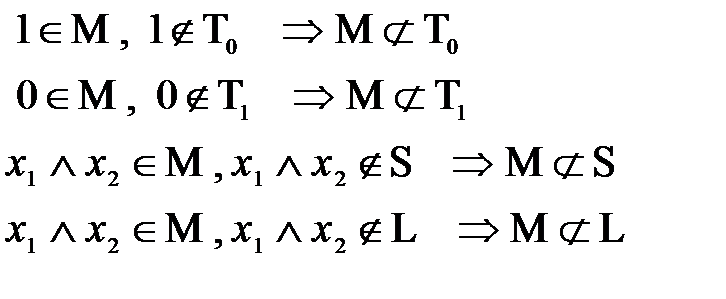
Рассмотрим 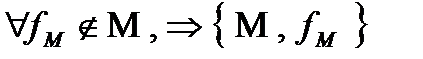 не принадлежит ни одному из пяти классов, следовательно по теореме Поста система полна, следовательно
не принадлежит ни одному из пяти классов, следовательно по теореме Поста система полна, следовательно 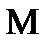 предполный.
предполный.
5) Рассмотрим L:
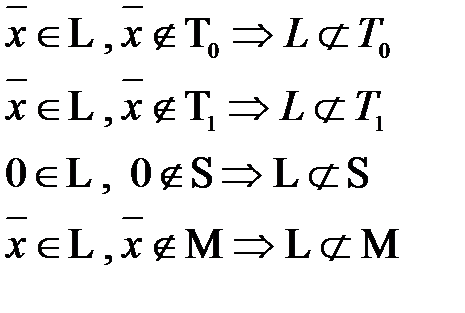
Рассмотрим 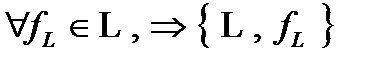 не принадлежит ни одному из пяти классов, следовательно по теореме Поста система полна, следовательно
не принадлежит ни одному из пяти классов, следовательно по теореме Поста система полна, следовательно 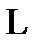 предполная. Все перечисленные классы не полны по теореме Поста.
предполная. Все перечисленные классы не полны по теореме Поста.
Покажем, что других предполных классов в 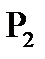 нет.
нет.
Допустим противное, что 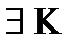 - предполный :
- предполный :
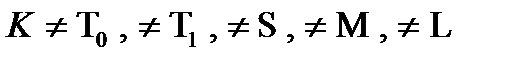 , следовательно в данном классе
, следовательно в данном классе 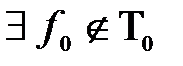 :
:
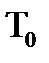 |
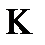 |
| РИС.1 |
в силу того, что класс 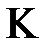 - предполный, следовательно включение на рис.1 невозможно, т.к. если бы было наоборот, то рассмотрим
- предполный, следовательно включение на рис.1 невозможно, т.к. если бы было наоборот, то рассмотрим 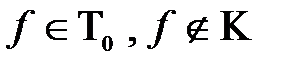 , мы бы получили, что все функции системы
, мы бы получили, что все функции системы 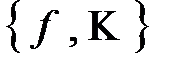 сохраняют 0, поэтому полной система
сохраняют 0, поэтому полной система 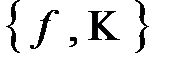 не является, следовательно
не является, следовательно 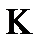 не является предполным.
не является предполным.
По этой же причине в классе 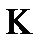 должна быть,
должна быть, 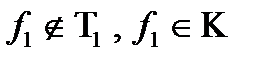 , должна быть
, должна быть 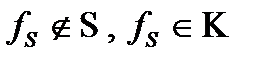 , должна быть
, должна быть 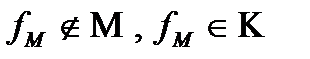 , должна быть
, должна быть 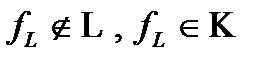 , следовательно из этих включений следует, что система
, следовательно из этих включений следует, что система 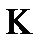 является полной, противоречие с предполнотой этой системы.
является полной, противоречие с предполнотой этой системы.
Упражнения:
Найдите определяющие выражения функций через суперпозиции функций системы.
1) 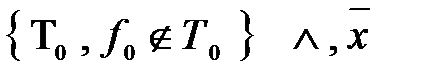
2) 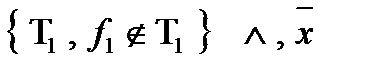
3) 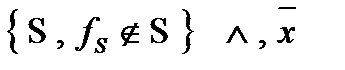
4) 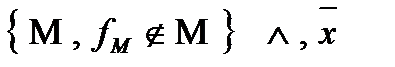
5) 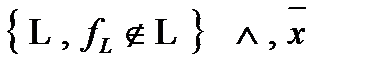
Определение:
Полной системой бул. функций в замкнутом классе К является система функций, которая принадлежит данному классу, и замыкание которой совпадает с самим классом
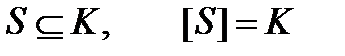 .
.
Определение:
Базисом в замкнутом классе К называют систему В, которая полна в этом классе, но любая собственная подсистема полной в классе не является.
Пример 1:Рассмотрим множество всех булевых функций Р2. В этом множестве рассмотрим систему 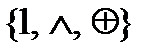 .Эта система полна по т. Поста .
.Эта система полна по т. Поста .
Чтобы определить,что все собственные подсистемы не полны, достаточно рассмотреть лишь максимальные по включению собственные подсистемы данной, получаемые из данной удалением какой-либо функции.
Если ни одна из этих подсистем не является полной, то полной не является и любая другая собственная подсистема (докажите предыдущие утвеждения)
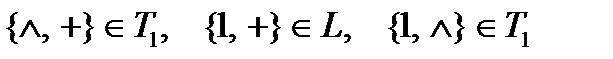
В данном примере максимальные собственные подсистемы не полны, значит 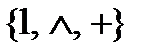 является базисом в Р2.
является базисом в Р2.
Пример 2:Является ли система 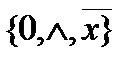 базисом в Р2?
базисом в Р2?
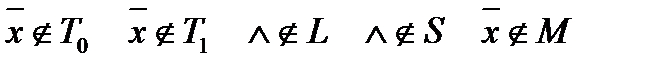 , поэтому система полна, но собственная подсистема
, поэтому система полна, но собственная подсистема 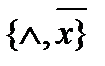 также полна, поэтому данная система не базис в Р2.
также полна, поэтому данная система не базис в Р2.
Определение:
Скажем, что функция f не зависима от системы 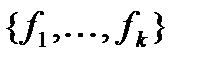 , если эта функция не принадлежит замыканию системы :
, если эта функция не принадлежит замыканию системы : 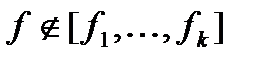 .
.
Пример 1: Рассмотрим функцию  и систему
и систему 
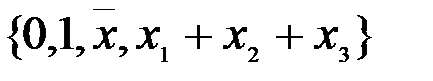 :
:
Утверждаем, что  не зависит от этой системы. Действительно, все функции системы являются линейными, поэтому в силу того, что суперпозиция линейных функций есть линейная функция, замыкание этой системы принадлежит классу линейных функций, а
не зависит от этой системы. Действительно, все функции системы являются линейными, поэтому в силу того, что суперпозиция линейных функций есть линейная функция, замыкание этой системы принадлежит классу линейных функций, а  — функция не линейная. Поэтому
— функция не линейная. Поэтому  не зависит от данной системы функций.
не зависит от данной системы функций.
Пример 2: Рассмотрим функцию  и систему
и систему 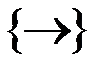 :
:
x1 x2 

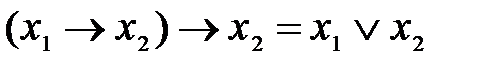
0 0 1 0 0
0 1 1 1 1
1 0 0 1 1
1 1 1 1 1
Значит,  зависима от функции
зависима от функции  .
.
Примечание: если функция не является независимой от системы, то будем называть ее зависимой от данной системы.
Утверждение:
Если система функций 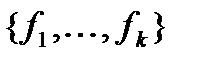 базис в замкнутом классе К , то тогда каждая функция базиса независима от оставшихся.
базис в замкнутом классе К , то тогда каждая функция базиса независима от оставшихся.
Доказательство:
Предположим противное: пусть существует базис 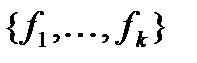 в котором некоторая функция является зависимой от оставшихся. Для определенности будем считать, что это
в котором некоторая функция является зависимой от оставшихся. Для определенности будем считать, что это 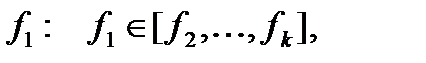 поэтому
поэтому 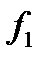 выражается через некоторые суперпозиции функций системы
выражается через некоторые суперпозиции функций системы 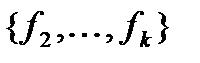 , но тогда система
, но тогда система 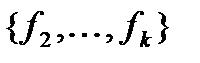 также является полной в классе К, поэтому
также является полной в классе К, поэтому 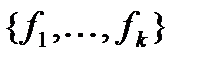 не является базисом. Утверждение доказано.
не является базисом. Утверждение доказано.
Пример 1:
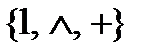 базис в Р2
базис в Р2

Упражнение:Докажите справедливость обратного утверждения: пусть 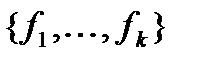 полная система в К, и любая функция системы не зависит от оставшихся, тогда система – базис в К.
полная система в К, и любая функция системы не зависит от оставшихся, тогда система – базис в К.
