IV. Конкуренция «новаторов» и «консерваторов»

Рассмотрим случай, когда один из производителей обладает технологической инновацией, существенно сокращающей производственный цикл (то есть, параметр τ)и/или снижающей себестоимость p̃.Этот случай соответствует модели Шумпетера борьбы новаторов и консерваторов.

Эта же задача актуальна в случае конкуренции отечественных производителей с импортерами, когда себестоимость импортного товара заметно ниже отечественного.

Рассмотрим первую задачу – случай, когда «новатор» не имеет средств для реализации инновации. Эти средства, в размере M̃, он берёт в кредит под процентную ставку κ̃. Средства M̃ частично расходуются на приобретение оборудования(средства M̃₀)и частично используются как оборотные для оплаты переменных расходов (обозначим последнее M̃₁⁽⁰⁾):

.

(40)

Величина M̃₁⁽⁰⁾ является начальным значением динамической переменной M₁.

При этом, «новатор» выплачивает проценты в размере κ̃M̃.Этому случаю соответствует модель (22), в которой «новатору» соответствует индекс 1, а «консерватору» – 2. Это значит, что p̃₁τ̃₁ < p̃₂τ̃₂,и в формулах (23) a₁ > a₂, c₁ > c₂.При этом, угол наклона изменён: tg ϕ > 1.

Выплаты по кредиту здесь играют роль постоянных издержек, то есть,

.

(41)

Фазовый портрет системы (22) с учётом упомянутых условий представлен на рис. 6. Портрет аналогичен рис. 2б. Отличие лишь в том, что угол наклона изоклин и величины κ₁ на рис. 6больше, чем на рис. 2б. Как и на рис. 2б имеется неустойчивое состояние – типа седла. Через него проходит сепаратриса (показана штрихпунктиром),разделяющая две области притяжения: M₂ = 0, M₁ = M_1,max,и M₁ = 0, M₂ = M_2,max.В первой «новатор» полностью вытесняет «консерватора», во второй, напротив,«новатор» сам вытесняется. Сепаратриса в левой части рисунка практически сливается с изоклиной вертикалей 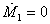.В максимуме последней сепаратриса отделяется от изоклины и ведет себя так же,как другие интегральные кривые (к семейству которых она принадлежит).

Рис. 6. Фазовый портрет системы (22) (с учётом выплат по кредиту)

Конкуренция «новаторов» и «консерваторов». См. пояснения в тексте.

Уравнение для сепаратрисы мы приводить не будем,поскольку для этого необходимо точное решение системы (22) в элементарных функциях. Последнее возможно отнюдь не всегда. Фазовый портрет системы (22)может быть построен с помощью компьютера (при заданных значениях параметров). В связи с этим, дальнейший анализ носит качественный характер, который опирается на топологические свойства фазового портрета.

Задача новатора – в начальный момент оказаться в области притяжения первого состояния. Это значит, что величина M₁⁽⁰⁾ должна находиться правее сепаратрисы. Это условие зависит от величины M₂.Если фирма-консерватор до появления новатора функционировала в стационарном режиме, то M₂ = M_2,max. В этом случае величинаM₁⁽⁰⁾, необходимая для вхождения в рынок, представлена на рис. 6 кружочком. Дальнейшая её динамика соответствует траектории,представленной штриховой линией. Вдоль этой траектории M₁(t) сперва падает,затем растёт и стремится к M₁ = M_1,max.Величина M₂(t) монотонно падает, вплоть до полного вытеснения с рынка.

Если величина M₁⁽⁰⁾ (взятая в кредит) лежит левее сепаратрисы (на рис. 6она представлена как M'₁⁽⁰⁾), то траектория системы (представленная пунктиром)– иная, и приводит к вытеснению «новатора» (при этом, нужно иметь в виду, что при меньшем M₁⁽⁰⁾, величина κ₁ тоже уменьшается, фазовый портрет деформируется, но его топология сохраняется).

Если сепаратриса проходит вблизи оси ординат, то необходимый кредит не очень велик и «новатор» может взять его под большие проценты.

Рассмотрим, вслед за Шумпетером, конкурентную борьбу«новатора» и «консерватора» в финансовой сфере.

Пусть новатор стартует с точки M₁⁽⁰⁾, M₂ = M_2,max.В любой момент t₁консерватор может взять кредит в размере M̃₂ (под проценты κ̃) с целью попасть в область притяжения своего предприятия. На рис. 6 эта точка представлена как M'₂. При этом его постоянные издержки повышаются.

Если время t₁ велико («консерватор» поздно опомнился), то кредит M̃₂ должен быть достаточно большим и, соответственно, велики постоянные издержки κ₂.В ответ на этот шаг, «новатор» вынужден взять дополнительный кредит и постоянные издержки его возрастут.

В результате, конкуренция на рынке кредитов приводит к непрерывному возрастанию постоянных издержек κ₁ и κ₂. Для каждой фирмы существуют критические постоянные издержки. Их можно оценить,используя формулы (7) и (8). Из них следует, что для существования фирмы должно выполниться условие

(42)

(индексы 1,2 соответствуют «новатору» и «консерватору»).

При возрастании величины κ̃ консерватору труднее выполнить условие (42), поскольку себестоимость p̃₂ выше.

Рассмотренный случай соответствует модели Шумпетера.

Отметим, что в процессе борьбы на рынке кредитов оборотные средства M₁и M₂возрастают. В то же время, цена товара p,согласно (21), падает. Это выглядит парадоксально, поскольку принято считать,что возрастание денежной массы ведет к ценовой инфляции. Обсуждаемая модель относится к микроэкономике. Поэтому, увеличение M₁ и M₂, строго говоря, не означает возрастание денежной массы в реальном секторе экономики по всей стране. Тем не менее, если подобная борьба происходит во всех отраслях, то эффект приобретает макроэкономические масштабы.

В заключение, отметим, что в настоящее время существует другой путь внедрения инноваций (венчурные фирмы), который не ведет к нарастанию постоянных издержек. При этом происходит разделение обязанностей.В качестве «новаторов» выступают ученые – разработчики инноваций. Труд по внедрению берут на себя другие агенты, в частности предприниматели–«консерваторы». Они уже обладают нужными средствами или берут их в кредит, но конкурентная борьба на финансовом рынке при этом не происходит.Конкуренция методу «новаторами» имеет место, но на уровне экспертного совета венчурной фирмы. В этой ситуации фирма–«консерватор» берёт кредит для модернизации производства (реализации инновации).