Энергетические соотношения на границе жидкость – жидкость и твердое тело – твердое тело
Рассмотрим соотношения энергий падающей и преломленной волн. Интенсивность для плоской бегущей гармонической волны:
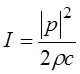 , (3.29)
, (3.29)
где 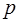 – давление в волне;
– давление в волне;
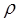 – плотность среды;
– плотность среды;
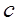 – скорость волны.
– скорость волны.
Для определения доли прошедшей и отраженной энергии нужно выделить компоненту потока энергии, нормально падающего на границу. Нормальная компонента интенсивности падающей волны:
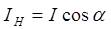 , (3.30)
, (3.30)
где 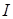 – интенсивность падающей волны. Нормальная компонента для преломленной волны:
– интенсивность падающей волны. Нормальная компонента для преломленной волны:
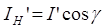 , (3.31)
, (3.31)
где 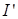 – интенсивность прошедшей волны. Отсюда коэффициент прозрачности по энергии:
– интенсивность прошедшей волны. Отсюда коэффициент прозрачности по энергии:
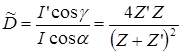 . (3.32)
. (3.32)
Сопоставление со значением коэффициента прозрачности по амплитуде показывает, что коэффициент прозрачности по энергии равен произведению значений 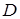 при прохождении через границу в прямом и обратном направлениях:
при прохождении через границу в прямом и обратном направлениях:
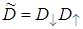 . (3.33)
. (3.33)
Это положение важно для дефектоскопии, поскольку при введении волн в объект контроля через какую-либо промежуточную среду, энергия обычно проходит через границу в двух направлениях. Оно остается справедливо для любых сред.
Коэффициент отражения по интенсивности:
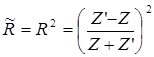 . (3.34)
. (3.34)
Энергетические соотношения для границы двух жидких сред:
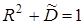 . (3.35)
. (3.35)
Для границы двух твердых тел соотношение 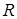 и
и 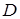 может быть получено путем обобщения для границы жидкость – жидкость.
может быть получено путем обобщения для границы жидкость – жидкость.
Для границы твердое тело – твердое тело коэффициент отражения по амплитуде
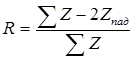 , (3.36)
, (3.36)
где 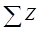 – сумма импедансов всех отраженных и преломленных волн. Это выражение может быть использовано для расчета отраженной волны, совпадающей по типу с падающей.
– сумма импедансов всех отраженных и преломленных волн. Это выражение может быть использовано для расчета отраженной волны, совпадающей по типу с падающей.
Коэффициент прохождения по энергии в этом случае
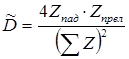 . (3.37)
. (3.37)
Выражение для 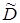 может быть использовано для расчета волны, несовпадающей по типу с падающей. Кроме того, данная формула применима как для границы твердое тело – твердое тело, так и для границы жидкость – жидкость.
может быть использовано для расчета волны, несовпадающей по типу с падающей. Кроме того, данная формула применима как для границы твердое тело – твердое тело, так и для границы жидкость – жидкость.
Нормальный акустический импеданс для продольной и поперечной волн соответственно:
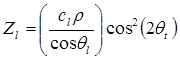 ,
, 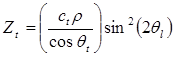 , (3.38)
, (3.38)
где 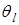 и
и 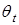 – углы между направлениями соответствующих волн и нормалью к поверхности.
– углы между направлениями соответствующих волн и нормалью к поверхности.
Критические углы
Если одна или обе среды – твердые тела, то из закона синусов вытекает возможность существования нескольких критических углов. Представим ситуацию, когда падающая волна продольная ( 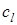 – скорость продольной падающей волны). В этом случае во второй среде может возникнуть два типа волн – прошедшая продольная со скоростью
– скорость продольной падающей волны). В этом случае во второй среде может возникнуть два типа волн – прошедшая продольная со скоростью 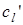 и прошедшая поперечная со скоростью
и прошедшая поперечная со скоростью 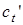 (рис. 3.4).
(рис. 3.4).
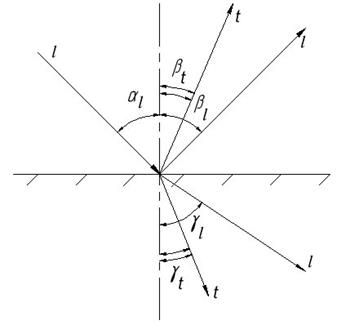 |
Рис. 3.4. Отражение и преломление волны на границе двух твердых сред: 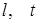 – продольная и поперечная волна, – продольная и поперечная волна, 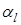 , , 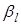 , , 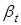 , , 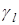 , , 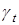 , – соответствующие углы падения, отражения, преломления , – соответствующие углы падения, отражения, преломления |
При этом возможна ситуация, когда 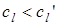 . Тогда при увеличении угла падения
. Тогда при увеличении угла падения 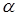 увеличивается и угол преломления
увеличивается и угол преломления 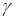 , и при определенном значении угла падения
, и при определенном значении угла падения 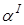 преломленная продольная волна сольется с границей раздела сред. Таким образом продольная волна во второй среде превращается в головную волну, распространяющуюся в поверхностном слое. Головная волна далее может быть использована для целей дефектоскопии. Такой угол падения называется первым критическим углом и определяется из условия
преломленная продольная волна сольется с границей раздела сред. Таким образом продольная волна во второй среде превращается в головную волну, распространяющуюся в поверхностном слое. Головная волна далее может быть использована для целей дефектоскопии. Такой угол падения называется первым критическим углом и определяется из условия
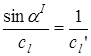 . (3.39)
. (3.39)
При углах падения больше либо равных 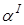 во вторую среду проходят только поперечные волны. Первый критический угол для границы оргстекло–сталь
во вторую среду проходят только поперечные волны. Первый критический угол для границы оргстекло–сталь 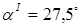 .
.
При выполнении условия 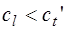 может возникнуть ситуация, когда при увеличении угла падения
может возникнуть ситуация, когда при увеличении угла падения 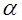 с границей раздела сред сольется преломленная поперечная волна. Такой угол падения
с границей раздела сред сольется преломленная поперечная волна. Такой угол падения 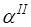 называется вторым критическим углом. Его значение рассчитывается из условия
называется вторым критическим углом. Его значение рассчитывается из условия
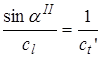 . (3.40)
. (3.40)
При втором критическом угле энергия падающей продольной волны переходит в энергию поверхностной волны Рэлея. Скорость такой волны равна 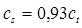 . Второй критический угол для границы оргстекло-сталь имеет значение
. Второй критический угол для границы оргстекло-сталь имеет значение 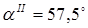 .
.
Третий критический угол существует, если из твердого тела на границу раздела сред падает поперечная волна со скоростью 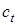 . Поскольку
. Поскольку 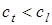 , то возможна ситуация, когда при определенном значении угла падения
, то возможна ситуация, когда при определенном значении угла падения 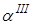 отраженная продольная волна сольется с поверхностью, превратившись в головную волну. Третий критический угол определяется из условия
отраженная продольная волна сольется с поверхностью, превратившись в головную волну. Третий критический угол определяется из условия
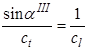 . (3.41)
. (3.41)
Третий критический угол для границы сталь-воздух равен 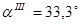 .
.
