Айталау сұрақтары. 1. Елестету арқылы орындалатын салу есептерін шығарудың жиі қолданылатын қандай дербес әдістерін білесіңдер?

1. Елестету арқылы орындалатын салу есептерін шығарудың жиі қолданылатын қандай дербес әдістерін білесіңдер?

2. Қарсы жору әдісінің мән-мағнасын түсіндіріңдер.

Дебиеттер

1. Рахымбек Д., Мадияров Н.К., Сейтжанова К.Б. Геометриялық салу есептері: Оқу құралы. Шымкент, «Нұрлы бейне», 2013. -287 бет

2. 1) Шыныбеков Ә.Н. Геометрия. Жалпы білім беретін мектептің 10-сыныбына арналған оқулық. Алматы, “Атамұра”, 2003. 2) Геометрия 11, 2005

3. Погорелов А.В. Геометрия: Жалпы бiлiм беретiн мектептiң 7-11 сыныптарына арналған оқулық. – 2-басылымы. Алматы: Просвещение-Қазақстан, 2003, 152 б.

Дәріс. Кеңістіктегі нүктелердің геометриялық орындары. Кеңістіктегі салу есептерін шығарудың нүктелердің геометриялық орындары әдісі.

Стереометриялық салу есептерiн шығарғанда геометриялық орындар жиi қолданылады. Геометриялық орын ұғымы үлкен әдiстемелiк мәнге ие және оқушылардың кеңiстiктiк түсiнiгi мен елестетуiн дамытуда үлкен орын алады. Кеңiстiктiк геометриялық орындар қолданылатын есептердi шығару оқушыларды кеңiстiктегi геометриялық фигуралардың бастапқыда қарапайым‚ кейiнiрек күрделiрек қатынастарын орнатуға үйретедi. Осыған ұқсас есептердi шығару оқушылардың кеңiстiктегi геометриялық денелердiң өзара қалай орналасқандығын‚ яғни қиылысады‚ жанасады немесе ортақ нүктесi жоқ болатындығын ойша елестетуiне алып келедi. Егер денелер қиылысса‚ онда олардың қиылысу сызығын ойша елестете отырып салады немесе моделден көрсетедi.

Анықтама. Берiлген қасиетке ие болатын, кеңiстiк (жазықтық) нүктелерiнiң геометриялық орны деп, кеңiстiктiң осы қасиетке ие болатын барлық нүктелерiнiң жиынын айтамыз.

Демек, Р фигурасы А қасиетке ие болатын нүктелердiң геометриялық орны болып табылатындығын дәлелдеу үшiн, мынадай екi сөйлемдi дәлелдеу керек:

1) Р фигурасының барлық нүктелерi А қасиетiне ие болады.

2) Р фигурасына тиiстi болмайтын ешқандай нүкте А қасиетiне ие болмайды.

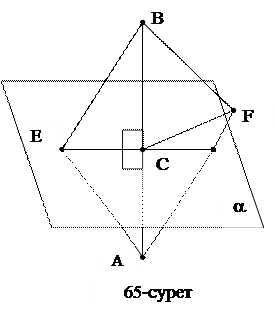
Мысалы. Берiлген екi нүктеден бiрдей қашықтықта жатқан нүктелердiң геометриялық орнын табу керек.

Шешуi. Iзделiндi нүктелердiң геометриялық орны, осы нүктелердi қосатын кесiндiнiң ортасы арқылы өтетiн және оған перпендикуляр жазықтық (65-сурет).

Осы тұжырымның дұрыстығын дәлелдеу үшiн, мынадай екi сөйлемдi дәлелдеймiз.

1) Е нүктесi a жазықтығының кез келген бiр нүктесi болсын. DАЕС=DВЕС болғандықтан АЕ=ВЕ болады.

2) Ендi a жазықтығынан тысқары жатқан кез келген нүктенiң А және В нүктелерiнен бiрдей қашықтықта жатпайтынын көрсету керек. Яғни, ҒÏa нүктесiн алсақ, онда DАҒВ үшбұрышында ҒС медиана болғанымен биiктiк бола алмайды. Олай болса, АҒ¹ҒВ. Тұжырым дәлелдендi.

Жазықтықтағы нүктелердiң геометриялық орны деп қандайда бiр қасиетке ие болатын барлық нүктелердiң жиынтығы айтылады. Жазықтықта тек нүктелердiң геометриялық орны қарастырылса‚ ал кеңiстiкте тек нүктелердiң геометриялық орны ғана емес сызықтардың да (түзулердiң және қисықтардың) геометриялық орны қарастырылады. Сондықтан кеңiстiктегi геометриялық орын деп қандай да бiр немесе бiрнеше анықталған шарттарды қанағаттандыратын барлық элементтердiң жиынтығын айтады.

Кеңiстiктегi геометриялық орындар өзiнiң мазмұны жағынан жазықтықтағы геометриялық орындарға қарағанда бай. Олардың кейбiрi жазықтықтағы нүктелердiң геометриялық орындарының кеңiстiктегi жалпылануы болып келедi. Мысалы‚ сфера – шеңбердiң‚ ал жазықтық - түзудiң және т.с.с. стереометриялық аналогтары болып табылады.

Кеңiстiктегi геометриялық орындарға берiлген есептердi мүмкiндiгiнше оған ұқсас жазықтықтағы нүктелердiң геометриялық орындарын еске түсiре отырып шығарған дұрыс. Бұл оқушылардың кеңiстiктегi геометриялық орындарды жақсы қабылдауы мен меңгеруiне мүмкiндiк бередi.

Жоғарыда айтылғандай‚ кеңiстiкте тек нүктелердiң ғана емес сол сияқты сызықтардың да (дербес жағдайда түзулер мен шеңберлердiң) геометриялық орындары да қарастырылады. Сондықтан бiр геометриялық образды нүктелердiң геометриялық орны ретiнде де‚ сол сияқты сызықтардың геометриялық орны ретiнде де қарастыруға болады. Мысалы:

I. a жазықтығына параллель және одан а қашықтықта орналасқан b және g жазықтықтары кеңiстiкте мынадай геометриялық орындарды анықтайды:

1) a жазықтығынан а қашықтықта орналасқан нүктелердiң геометриялық орны;

2) a жазықтығына параллель және одан а қашықтықта орналасқан түзулердiң геометриялық орны:

II. MN кесiндiсiнiң ортасы арқылы өтетiн және оған перпендикуляр жазықтық кеңiстiктегi мынадай геометриялық орындарды бередi:

1) Кесiндiнiң ұштарынан бiрдей қашықтықта орналасқан нүктелердiң геометриялық орны;

2) MN кесiндiсiне перпендикуляр және оның ортасы арқылы өтетiн түзулердiң геометриялық орны;

3) Центрлерi M және N нүктелерi болатын бiрдей 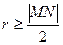радиусты сфералардың қиылысу шеңберлерiнiң геометриялық орны‚ - болады.

Стереометриялық салу есептерiн шығару барысында геометриялық орындар әдiсiн пайдалану мынадай жоспар бойынша жүргiзiледi. Бiрiншi, есеп шартына сәйкес берiлгендердiң бiрiн ғана ескерiп, басқаларын уақытша қалдыра тұрамыз. Ол шартқа сәйкес геометриялық орындар қандайда бiр кеңiстiктiк беттi бередi. Ендi есеп берiлгендерiнен тағы да бiр екiншi шартты ескерсек, бұл екi шартты қанағаттандыратын геометриялық орындар сол екi кеңiстiктiк беттердiң қиылысу сызығы болады. Тағы да сол сияқты, есеп берiлгендерiнен үшiншi шартты алсақ, бұл шарттарды қанағаттандыратын геометриялық орын қандайда бiр немесе бiрнеше нүктелер болады. Егер осы шарттарды қанағаттандыратын геометриялық орындардың ортақ нүктелерi жоқ болса, онда есептiң шешiмi болмайды.

Есептiң берiлген элементтерiнiң әр түрлi орналасу жағдайына талдау жасалып, есеп шартын қанағаттандыратын нүктелердiң, түзулердiң, жазықтықтардың және т.с.с. орналасуы мен саны анықталады. Есептiң алынған шешiмiн зерттеу барысында мүмкiн болатын беттер мен денелердi ойша әр түрлi жағдайда орналастыра отырып, олардың қиылысу немесе жанасу сызықтарының (нүктелерiнiң) формалары анықталады. Және керiсiнше, ол беттер қиылысатын, жанасатын немесе ортақ нүктелерi болмайтындай етiп қалай орналастыруға болатындықтары зерттеледi.

Стереометриялық салу есептерiн шығаруда осындай зерттеулер жасау оқушылардың кеңiстiктiк түсiнiктерiн қалыптастыруға және дамытуға жақсы ықпал етедi.

Мысалы. а түзуiнiң бойынан, өзара параллель 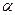және жазықтықтарынан бiрдей қашықтықта жатқан нүктенi салу.

Шешуi. Параллель 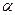және 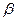жазықтықтарынан бiрдей қашықтықта жатқан нүктелердiң геометриялық орны, осы жазықтықтардан бiрдей қашықтықта жатқан және олардың әрбiрiне параллель 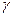жазықтығы. Олай болса, iзделiндi нүкте 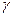жазықтығы мен а түзуiнiң қиылысу нүктесi болады.

Бiрақ бұл шешiм а түзуi 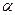, 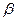жазықтықтарына параллель емес болған жағдайда ғана дұрыс. Егер а|| 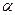болса, онда мынадай екi жағдай орындалуы мүмкiн.

1) а түзуi a және b жазықтықтарынан әр түрлi қашықтықта орналасқан‚ онда а түзуi мен g жазықтықтарының ортақ нүктесi болмайды. Сондықтан‚ есептiң шешiмi жоқ.

2) а түзуiнiң барлық нүктелерi a және b жазықтықтарынан бiрдей қашықтықта орналасқан‚ онда а түзуi g жазықтықтарында жатады. Демек‚ есептiң шешiмi болатын нүктелер (барлық а түзуiнiң нүктелерi) шексiз көп.