Функция и плотность распределения двумерной случайной величины

Функцией распределениявероятностей двумерной случайной величины интегральной функции называют функциюF(x,y), определяемую соотношением:

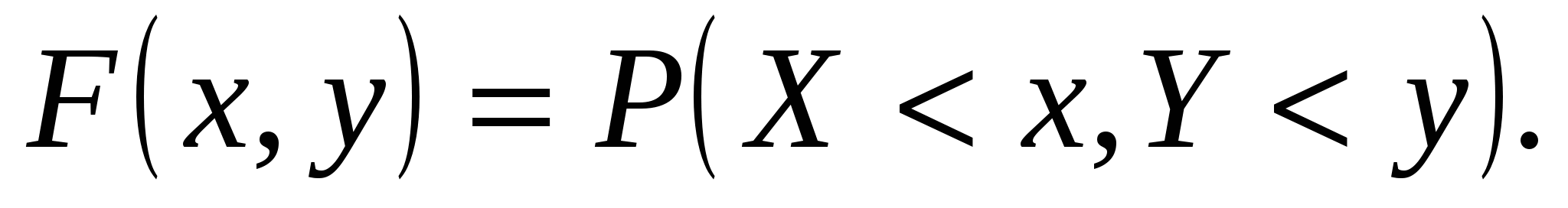
Она является неубывающей функцией и обладает следующими свойствами:

1. 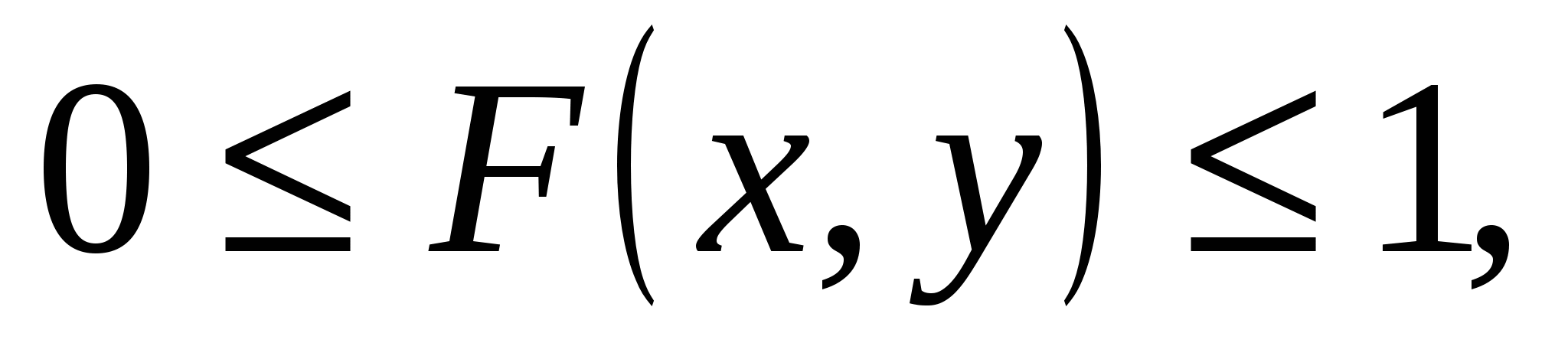при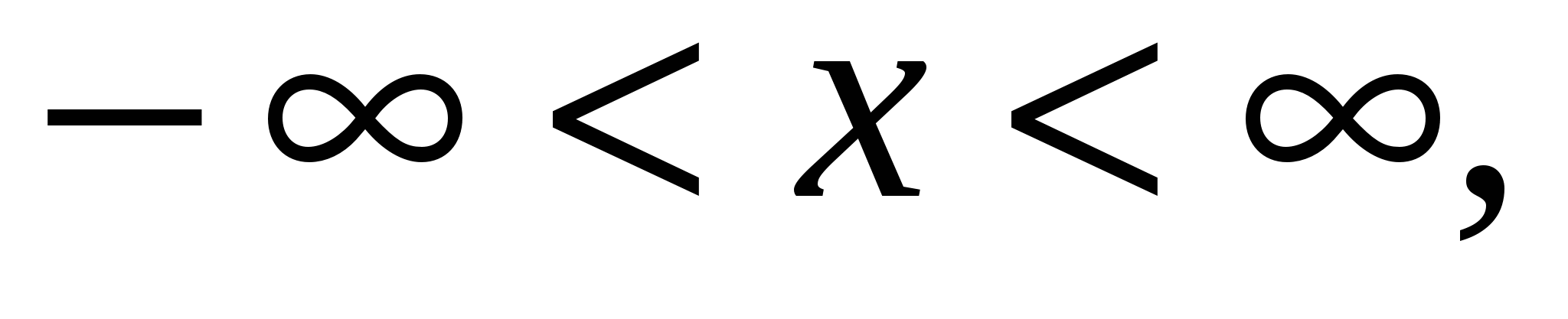

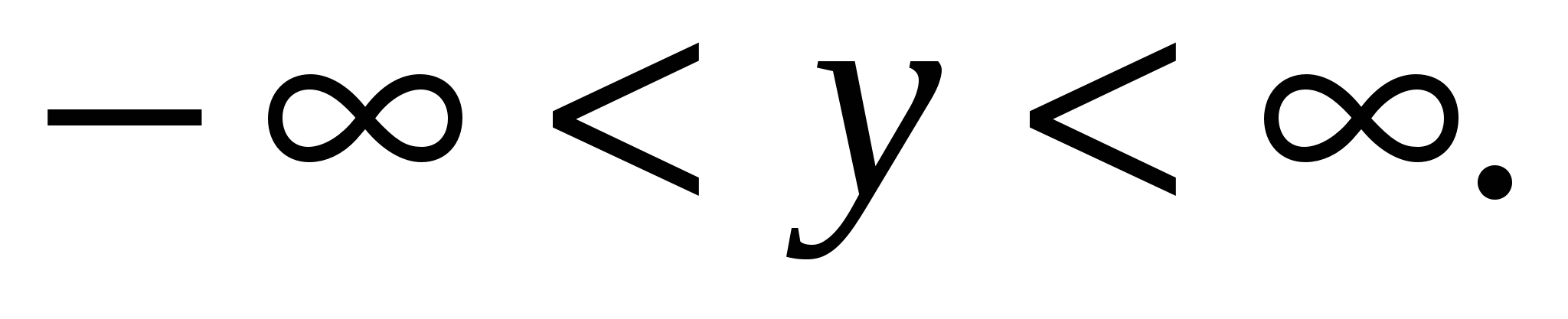
2.

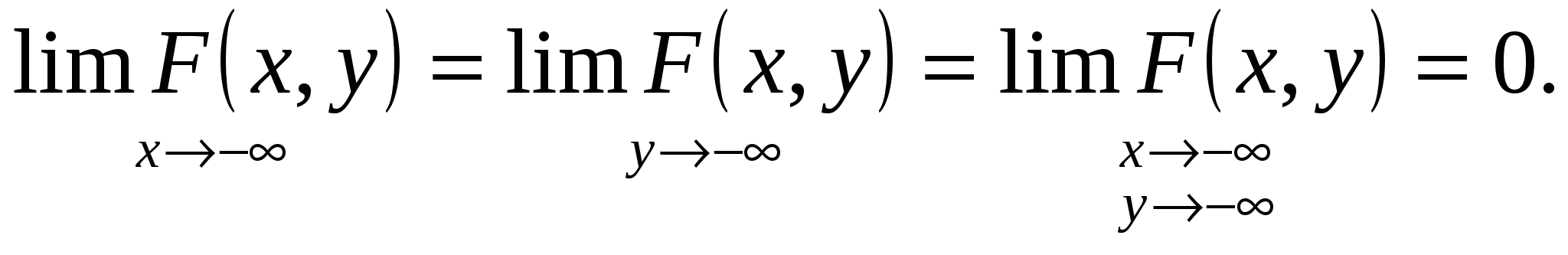
3.

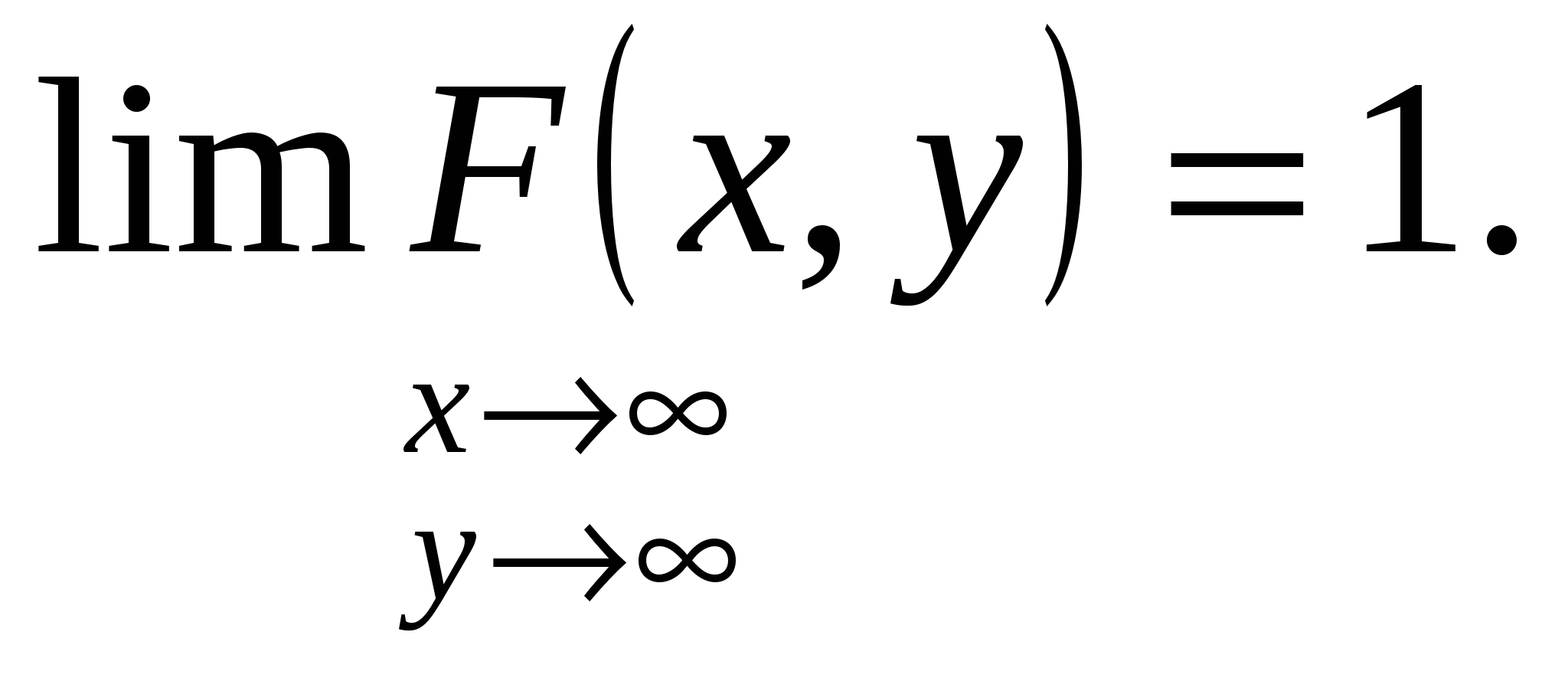
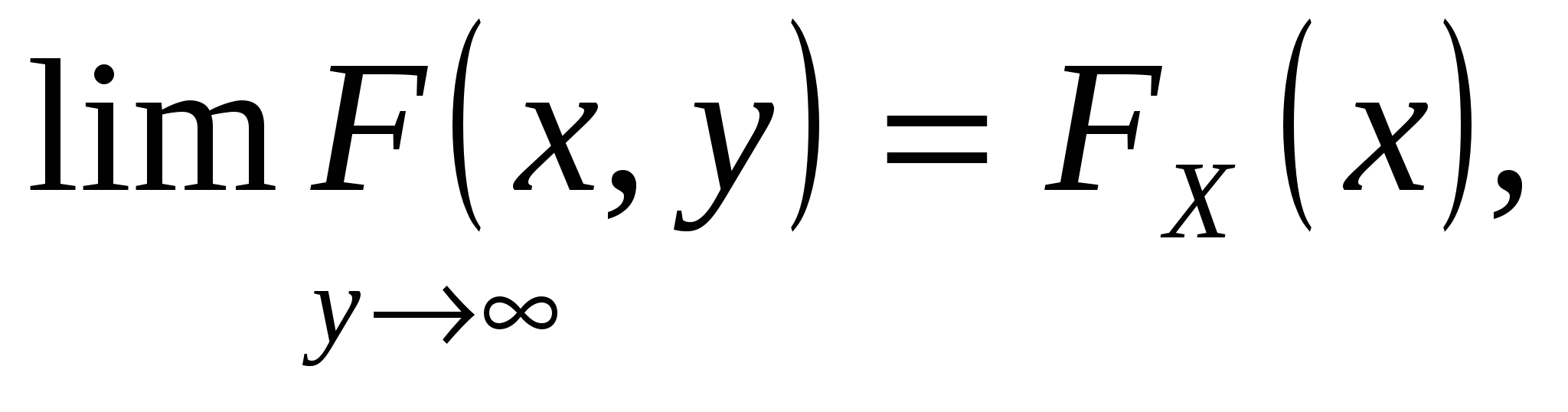
4. 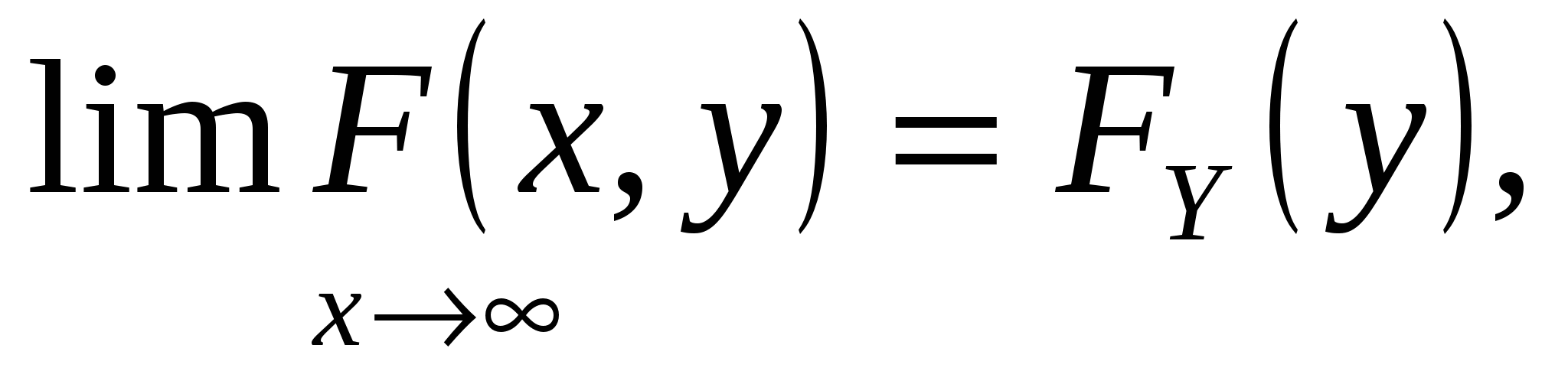где F_X(x) – функция распределения составляющейX, аF_Y(y) – составляющейY.

5.Вероятность попадания случайной точки в прямоугольник 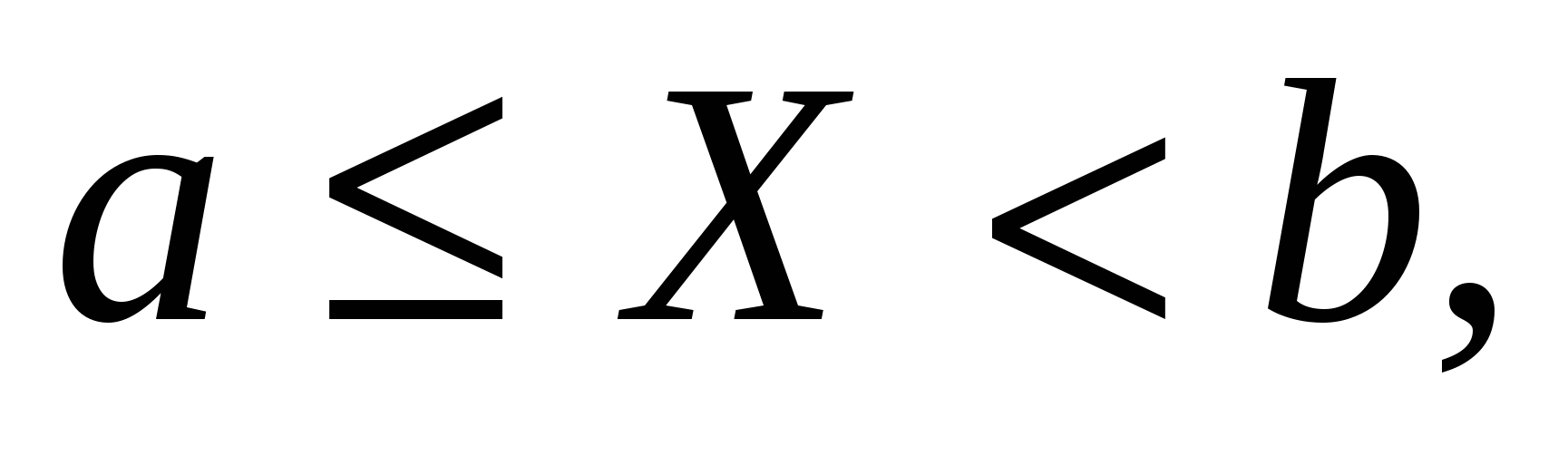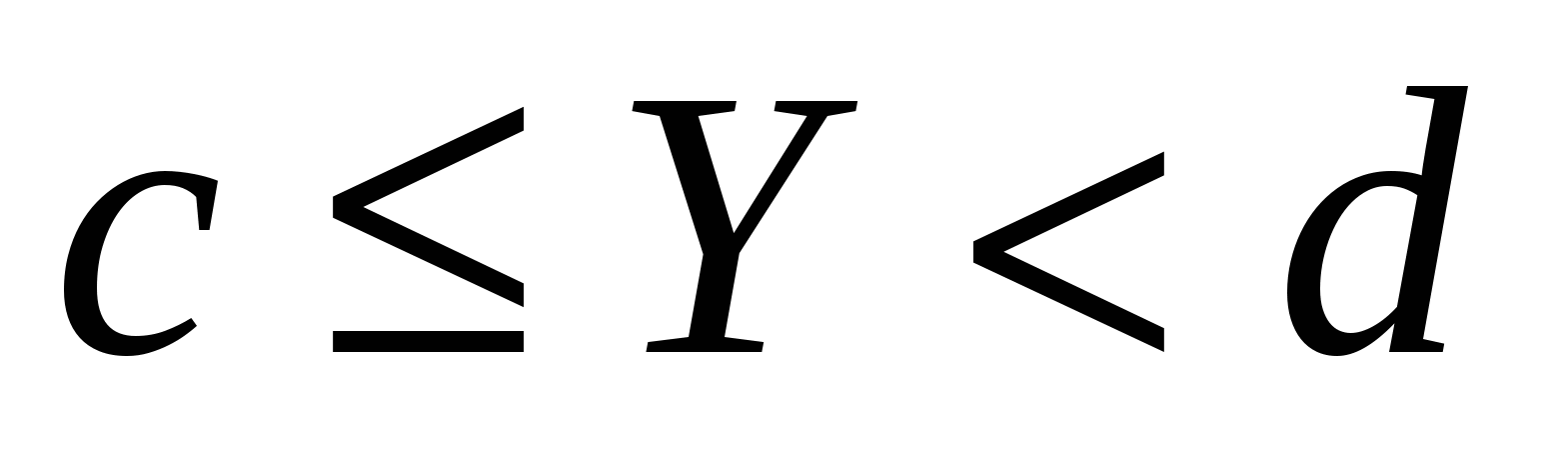вычисляется по формуле:

_.

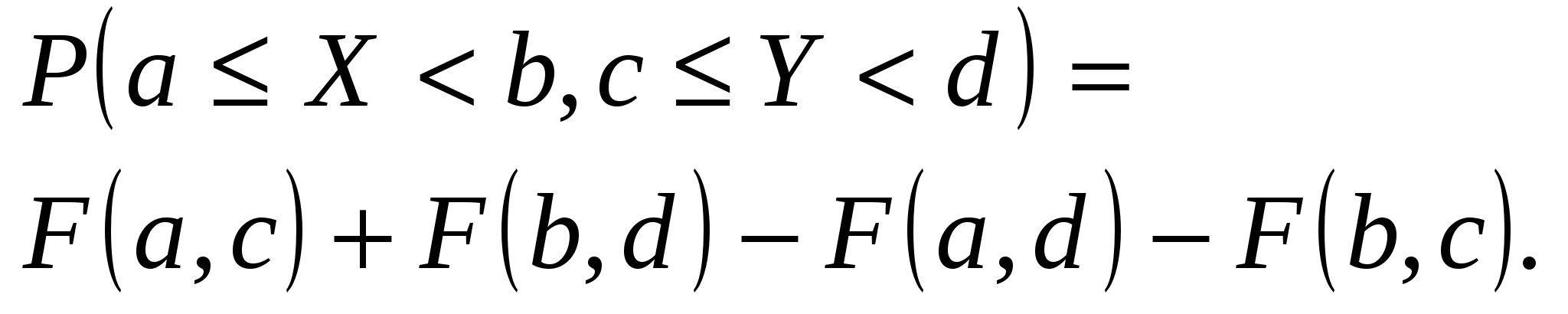Плотностью совместного распределениявероятностей случайного вектора (X,Y) называют вторую смешанную производную от функции распределения:

_.

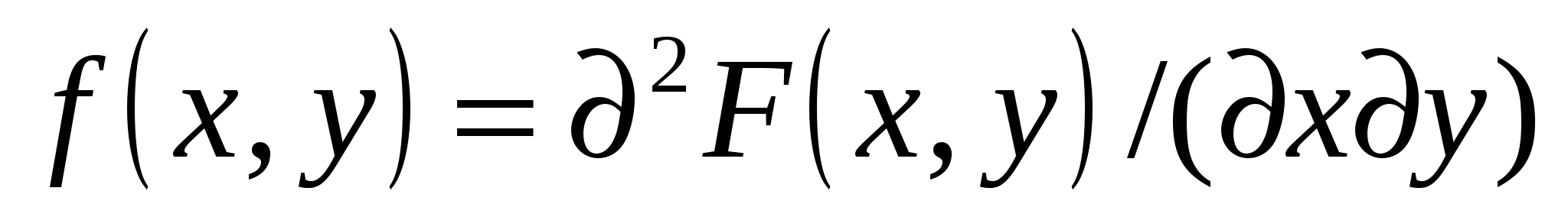Свойства совместной двумерной плотность распределения аналогичны свойствам плотности распределения вероятностей одной случайной величины:

1.

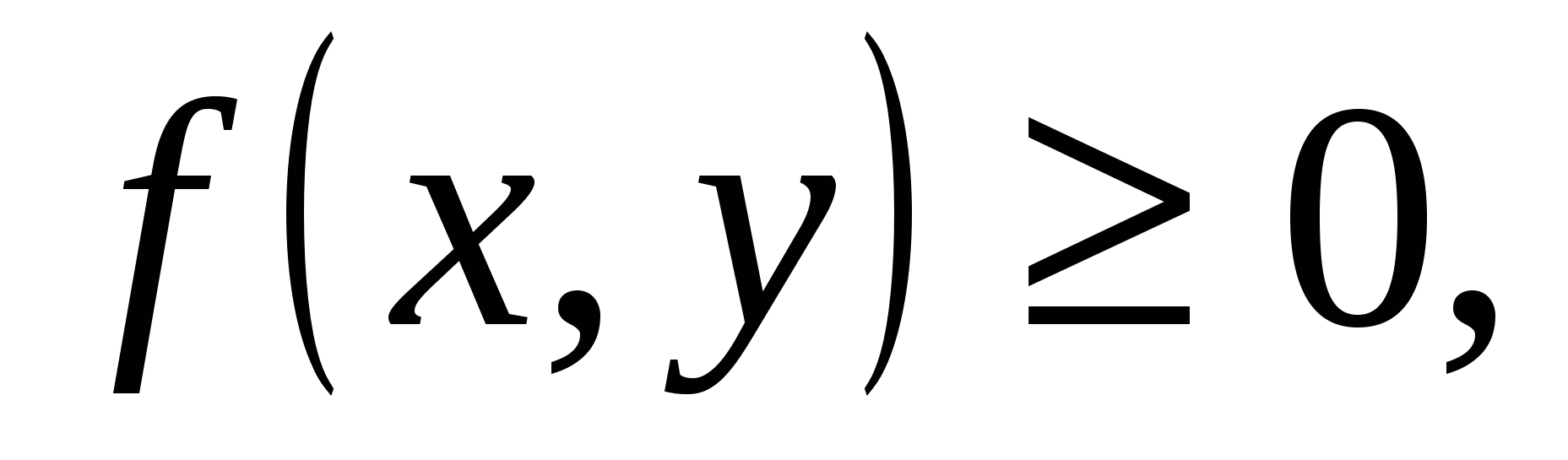
2.

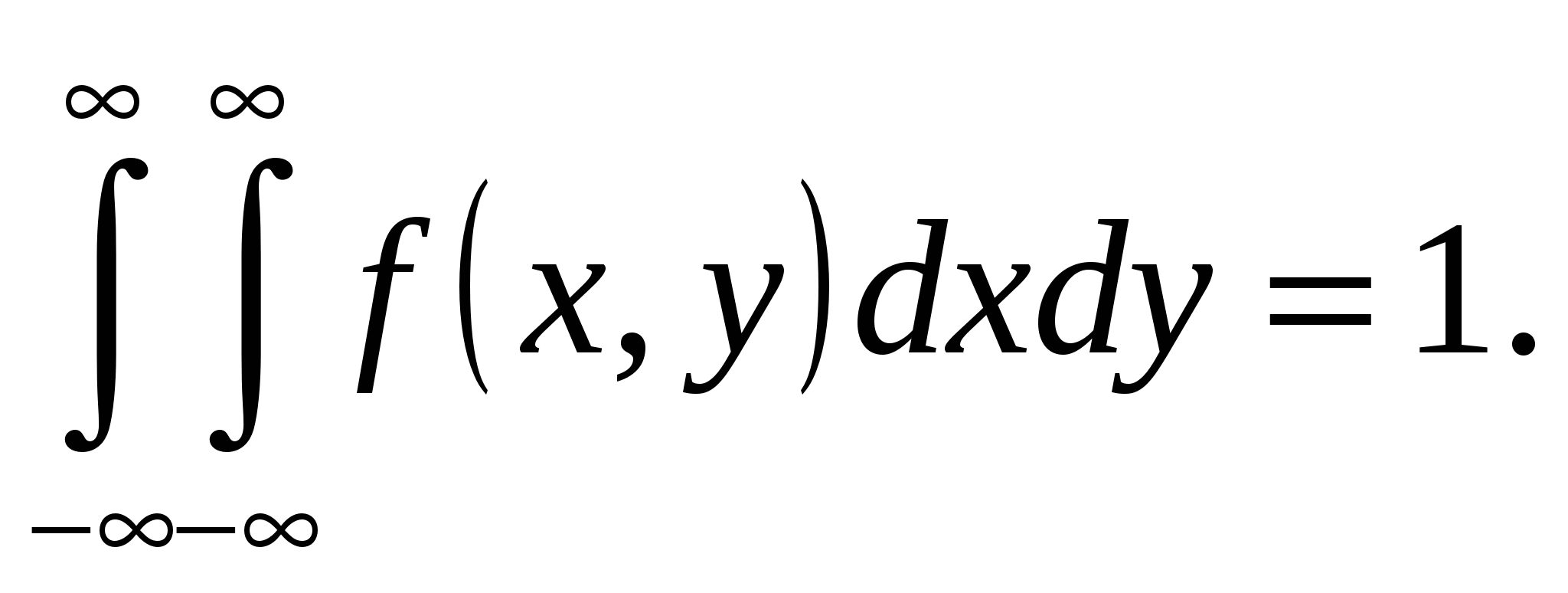
3.

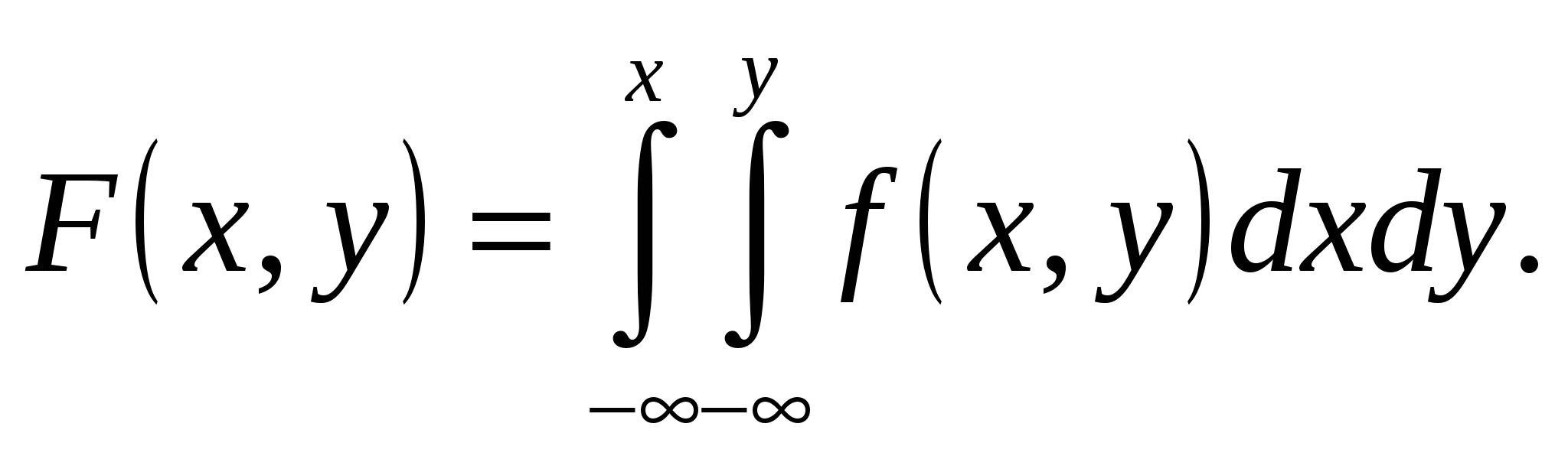
4.

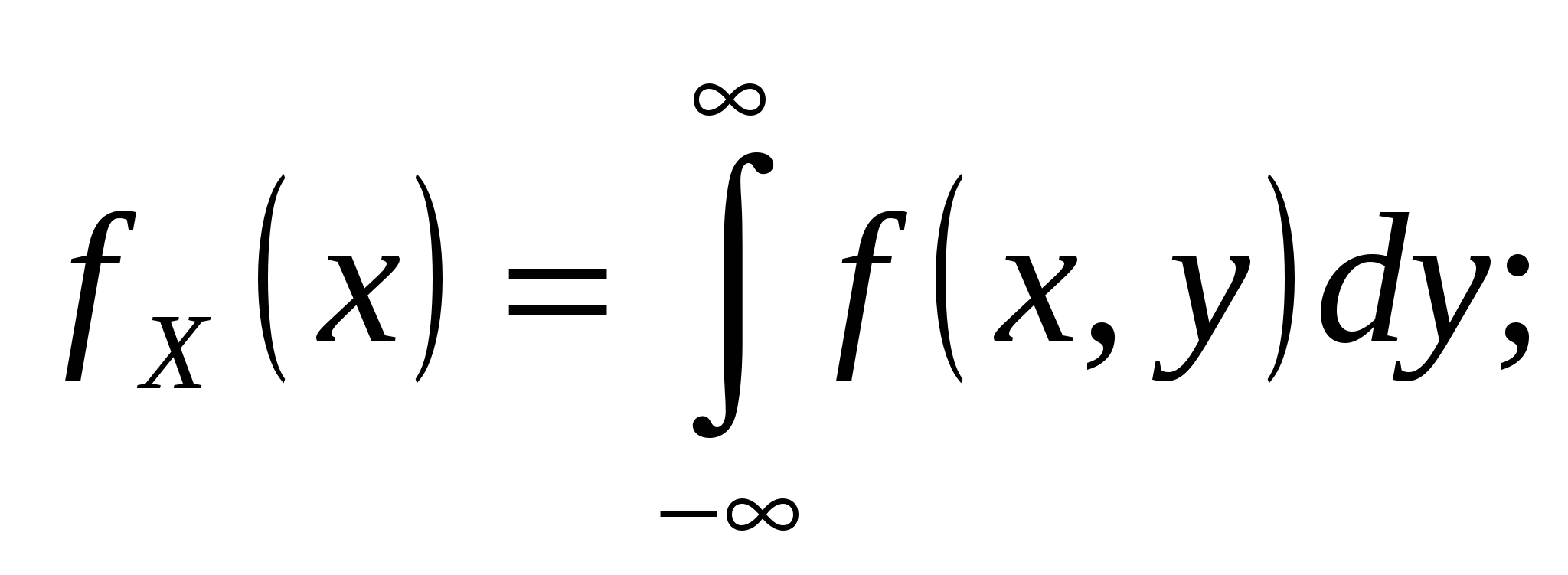
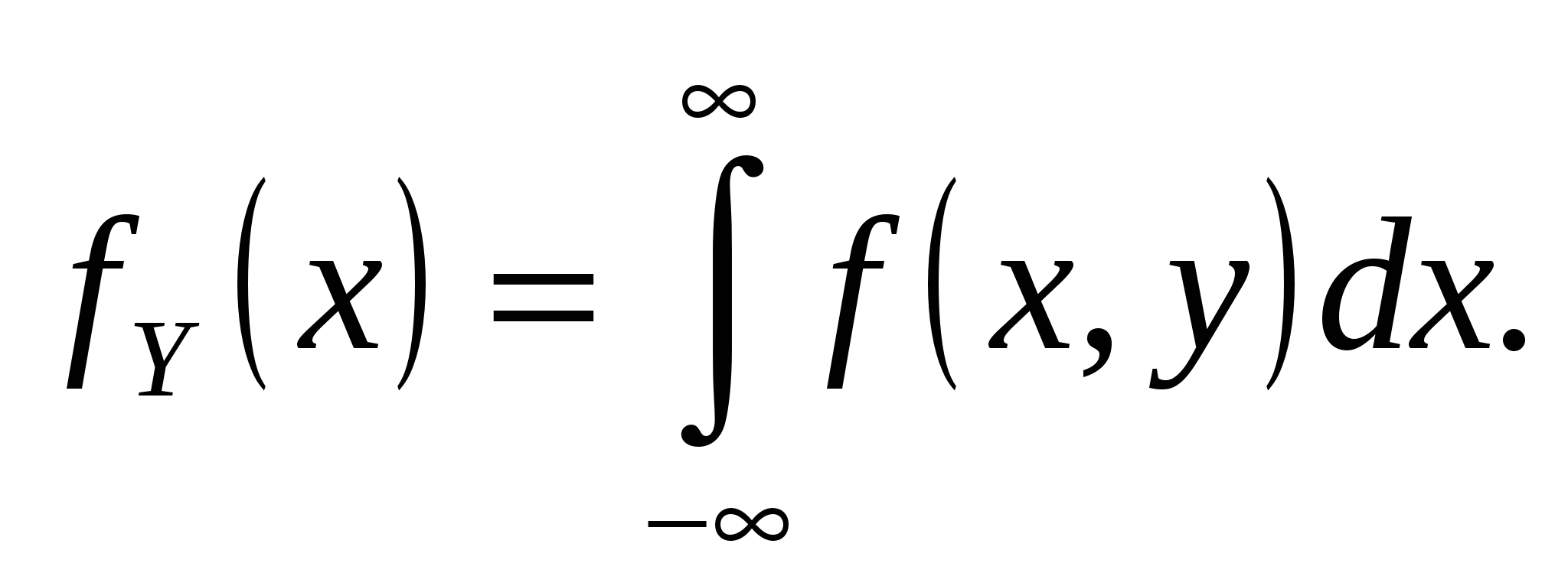
5.

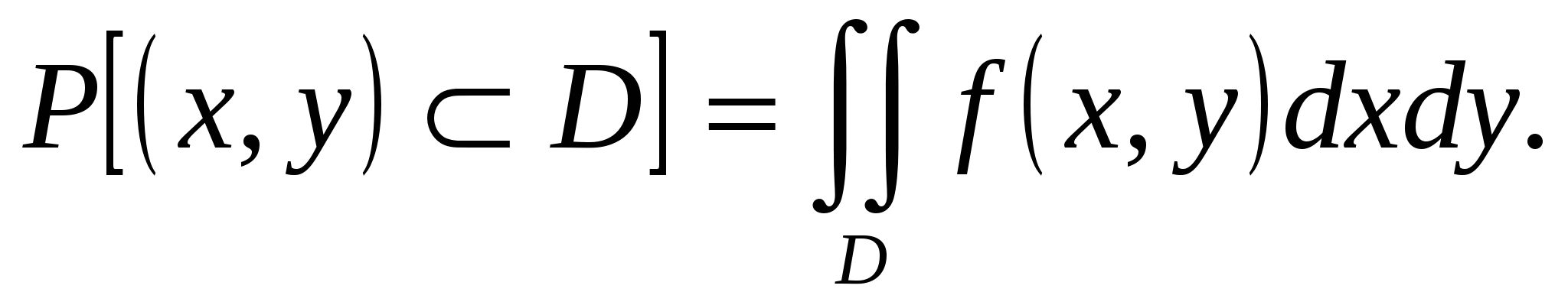
Условной плотностью распределения, составляющейXпри заданном значенииY=yназывается функция

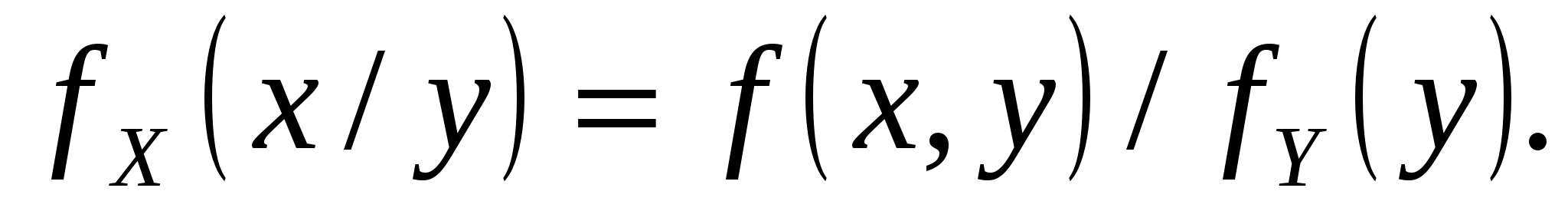
Аналогично:

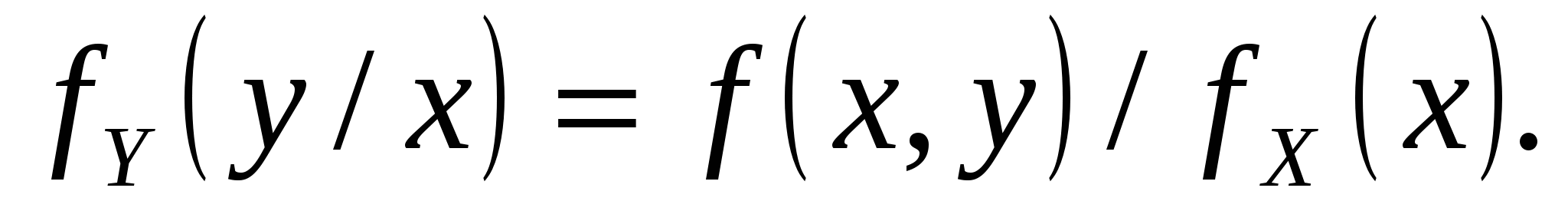
Если условые плотности распределения случайных величин Х,Yравны их безусловным плотностям, то такие величины называют независимыми.

Пример 10.Задан закон распределения вероятностей двумерной случайной величины (X,Y).

yk xj	-1
-2	0.1	0.2	0.15
	0.2	0.1	0.25

Найти: а) законы распределения составляющих; б) условный закон распределения Xпри условии, чтоY=-2; в) условный закон распределенияY, при условии, чтоX=2.

Решение.а) Для отыскания вероятностей появления возможных значений х_iпроведем суммирование вероятностей по существующим столбцам, а для y_k– по строкам. Результаты вычислений занесем в таблицу. Тогда первая и четвертая строки будут определять закон распределения для X, а первый и пятый столбцы – для Y.

N
	yixi	-1			P(Yk)	P(Yk/X=2)
	-2	0,1	0,2	0,15	0,45	3/8
		0,2	0,1	0,25	0,55	5/8
	p(xi)	0,3	0,3	0,4	∑=1
	P(Xi/Y=-2)	2/9	4/9	1/3	∑=1

б) Для отыскания условных вероятностей значений X поделим вероятность совместного появления X=x_i, Y=-2, на p(y_k=-2)=0,45 и результат запишем в последней строке: 0,1/0,45=2/9; 0,2/0,45=4/9; 0,15/0,45=1/3.

в) Аналогично найдем условные вероятности для Y: 0,15/0,4=3/8; 0,25/0,4=5/8.

Тогда первая и пятая строки будут определять условный закон распределения для X, а первый и шестой столбцы – для Y.

Пример 11.Задана функция распределения двумерной случайной величины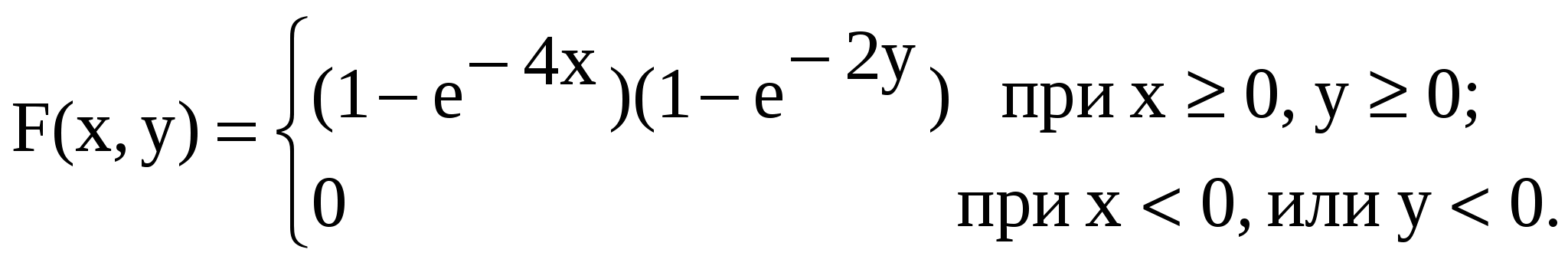

Найти: а) двумерную плотность распределения систему (X,Y); б) плотность распределения составляющих; в) условные плотности распределения составляющих; г) вероятность попадания случайной точки (X,Y) в треугольник с вершинами О(0,0); А(0,1); В(1,0).

Решение.а) Двумерную плотность вероятности системы найдем по формуле: 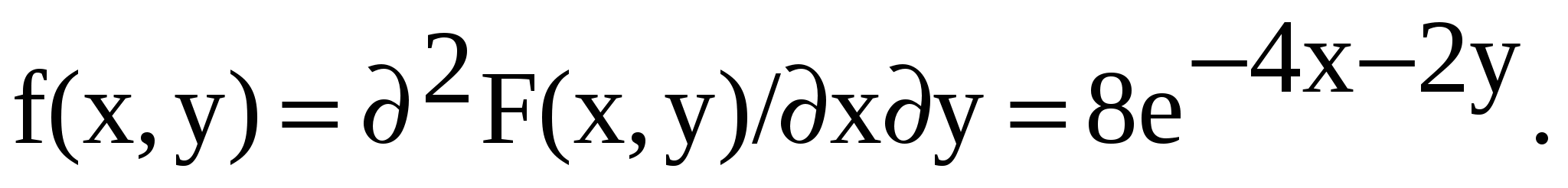Следовательно

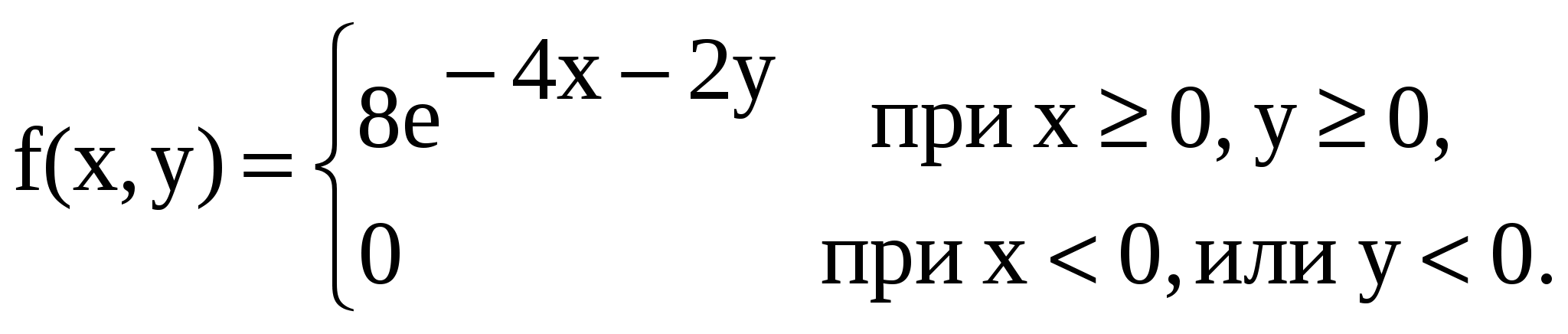
б) Найдем плотность распределения составляющей X:

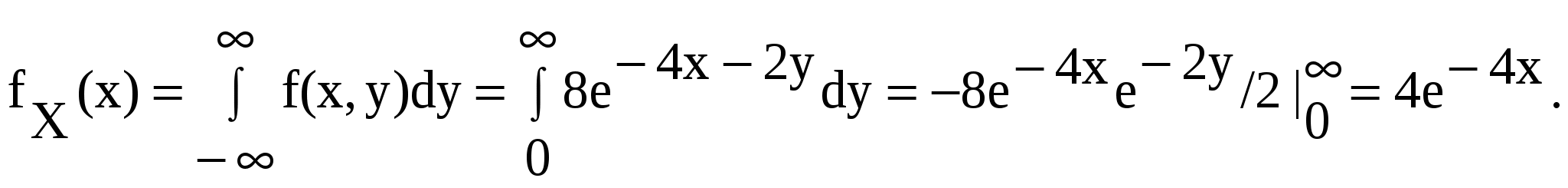
Для составляющей Y:

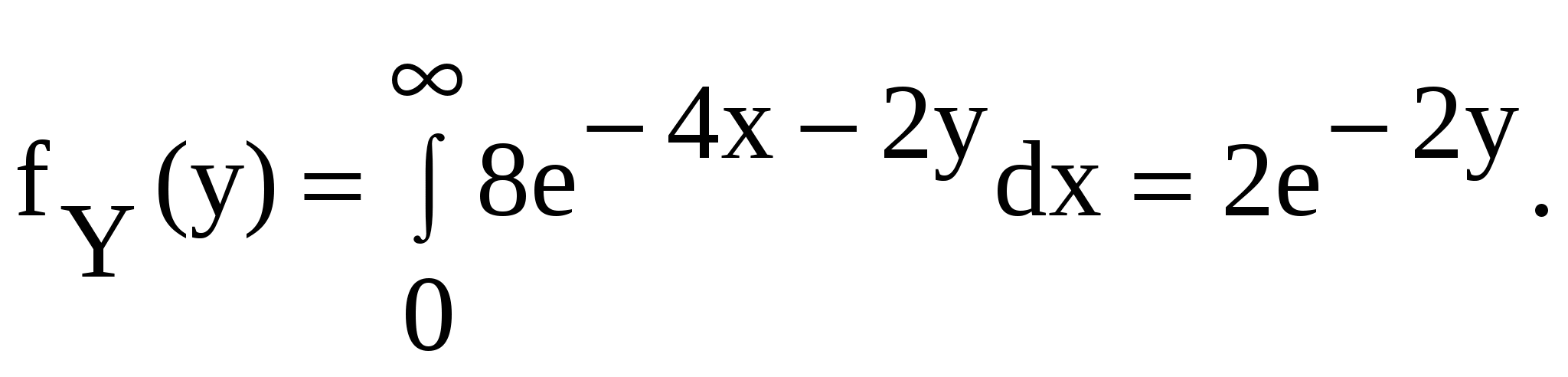
в) Условные плотности распределения равны:

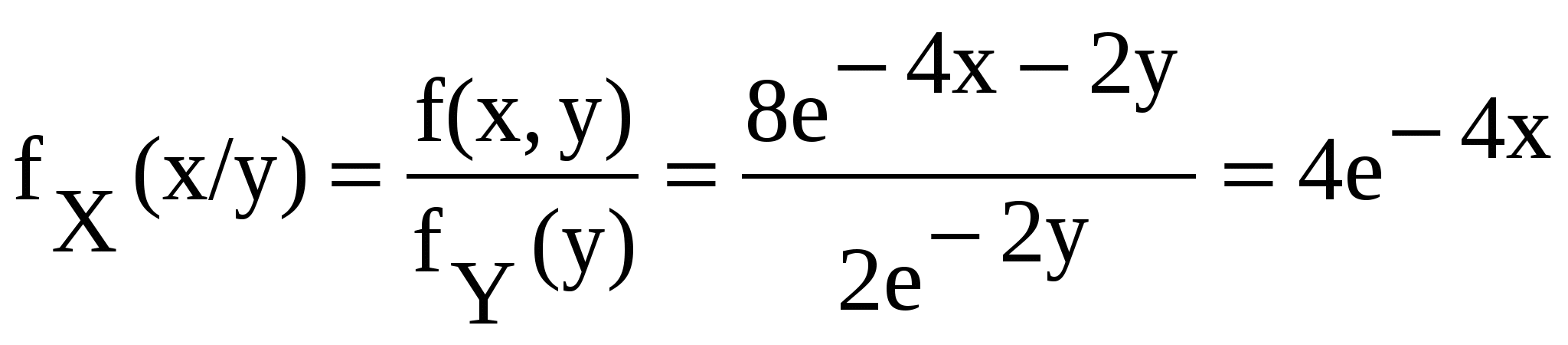
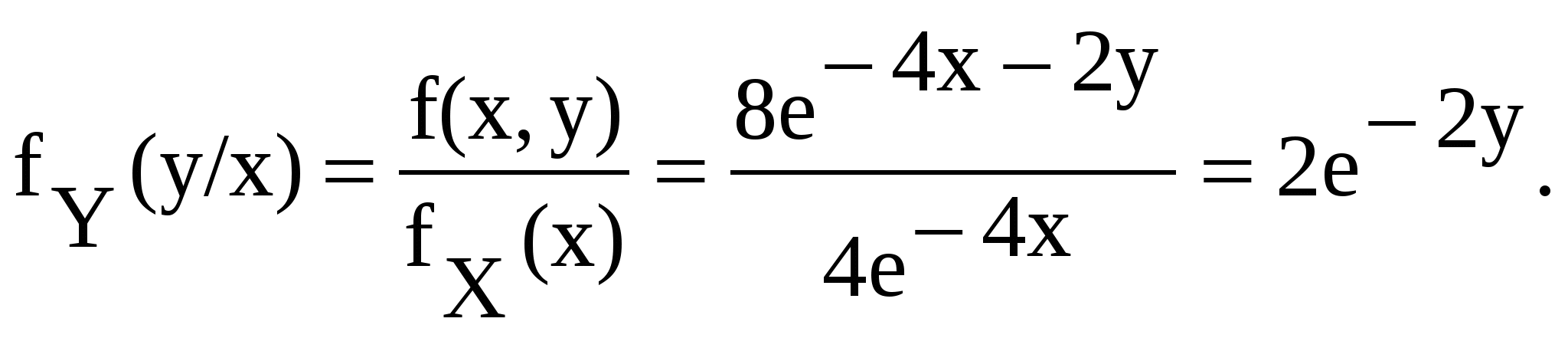
Заметим, что условные плотности распределения совпали с безусловными, следовательно X и Y независимы.

г) Вероятность попадания случайной точки в область Д вычисляется по формуле: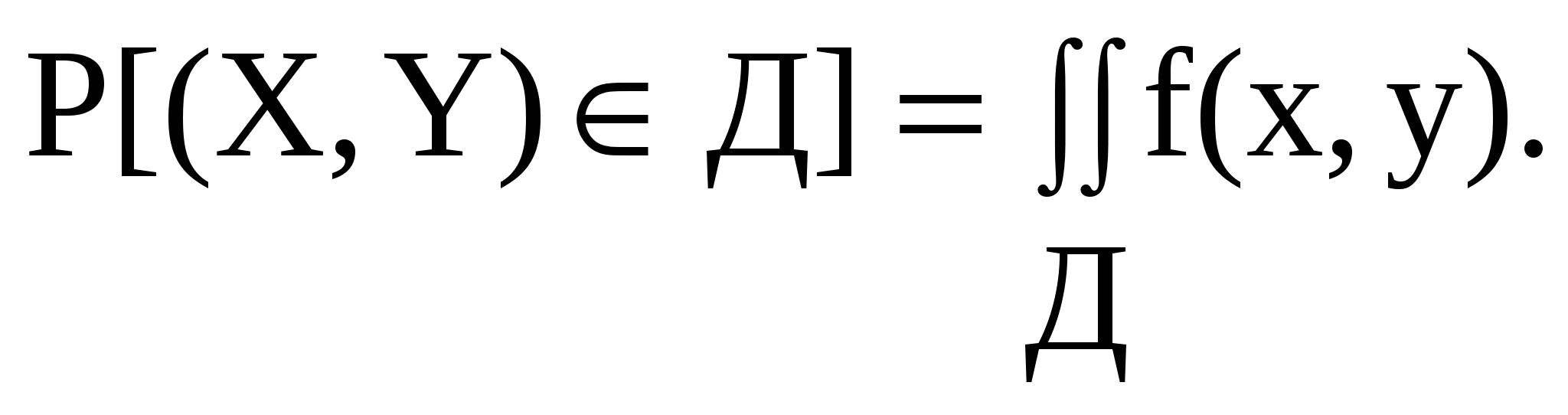

Область Д – треугольник ОАВ, уравнения сторон которого имеют вид: x=0; y=0; x+y=1. Тогда

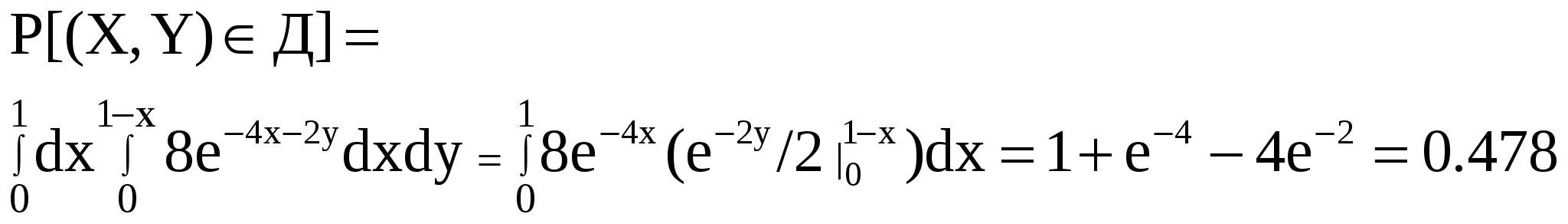
12. Задана двумерная плотность вероятности системы двух случайных величин: f (х, у) = (1/2)sin(х+у) в квадрате 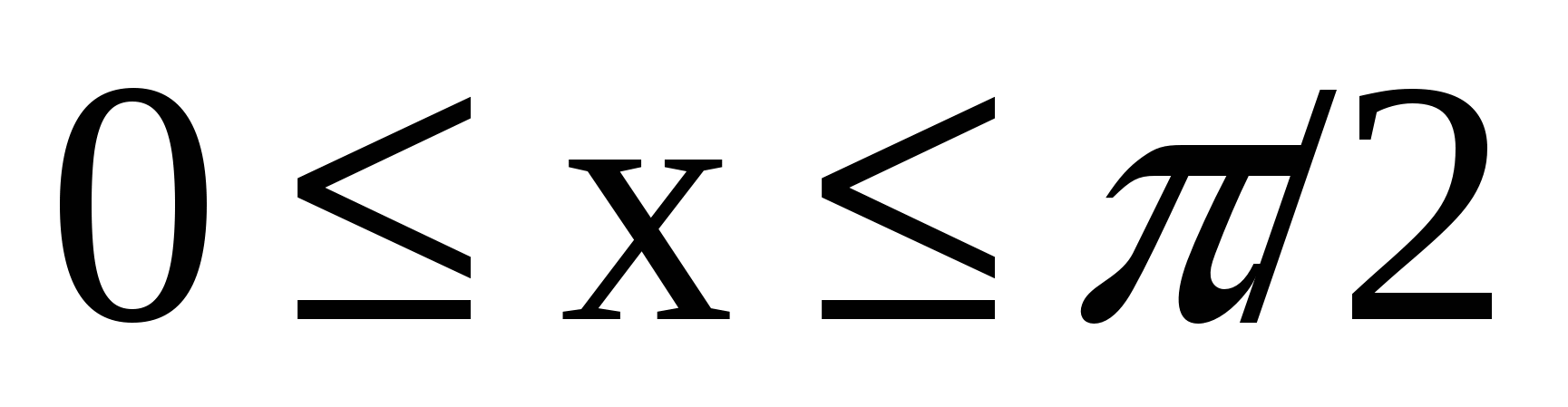, 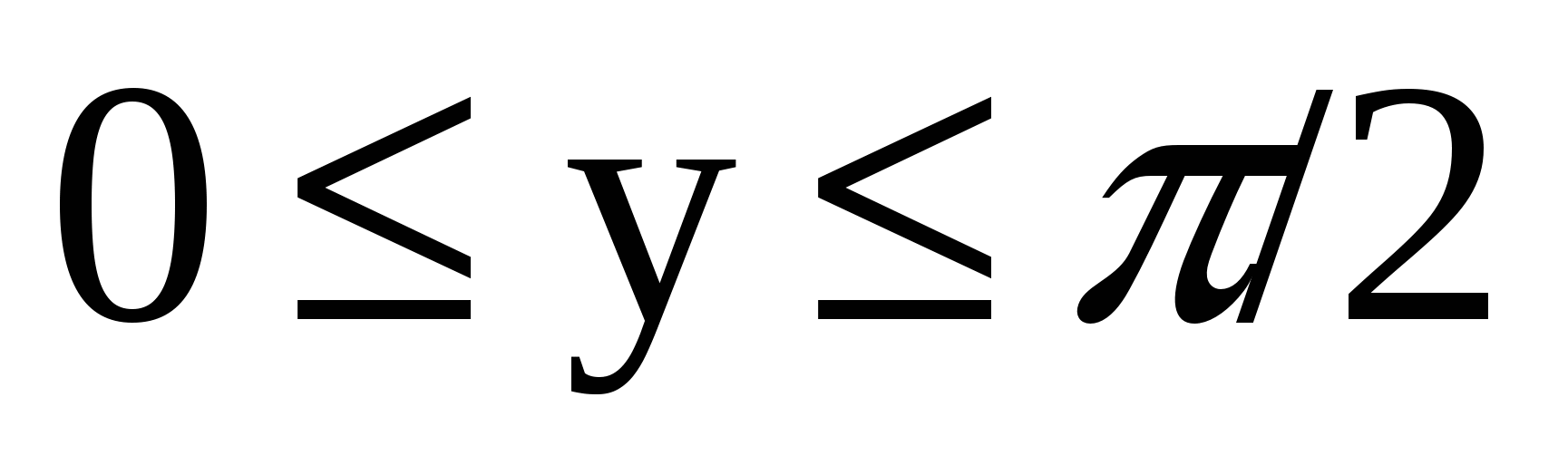; вне квадрата f(x,y)= 0. Найти функцию распределения системы (X, Y).

13. Задана двумерная плотность вероятности системы случайных величин (X, Y)

.

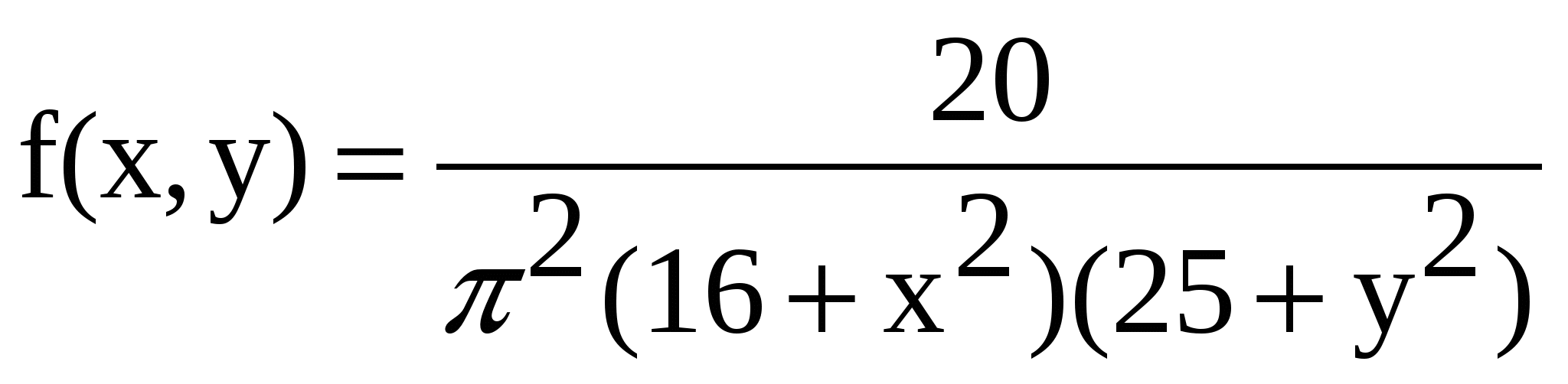Найти функцию распределения системы.

Указание: использовать формулу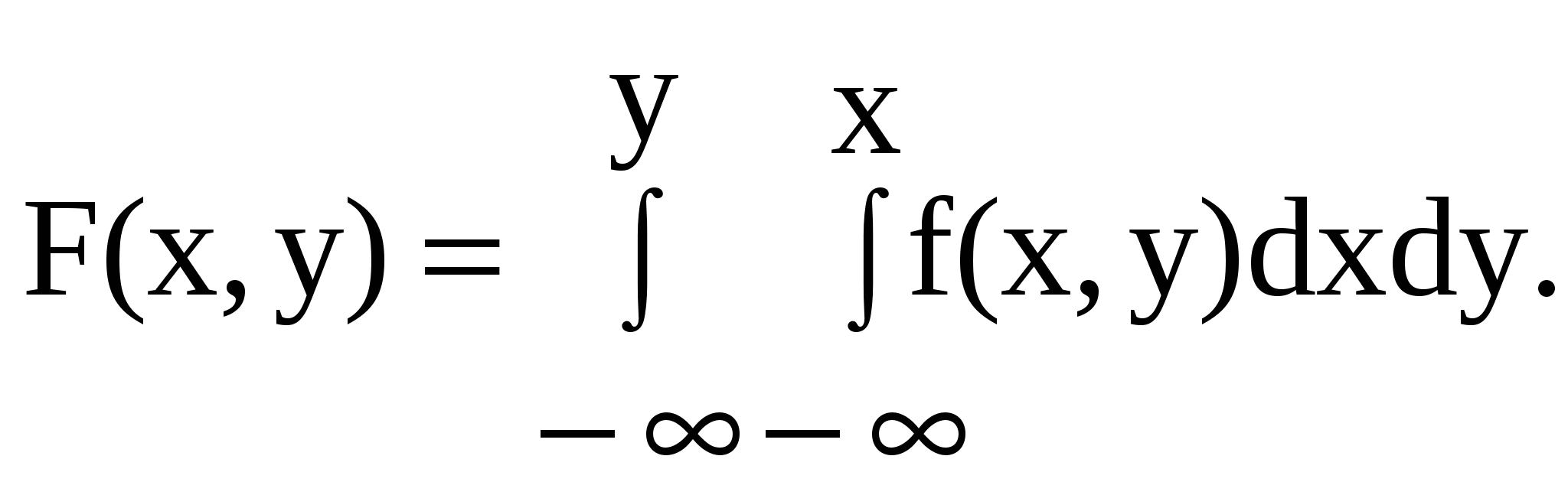

14. Задана двумерная плотность вероятности 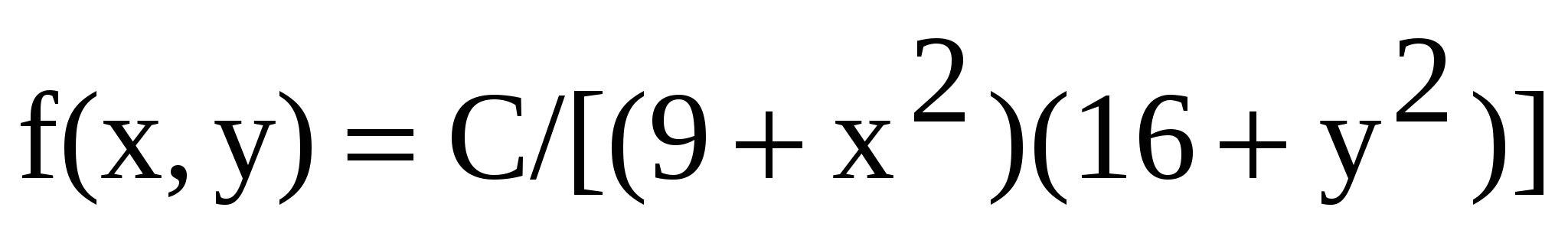системы (X, Y) двух случайных величин. Найти постоянную С.

15. Задана дискретная двумерная случайная величина (Х, Y):

Y	X
	0,25	0,10
	0,15	0,05
	0,32	0,13

Найти: а) условный закон распределения X при условии, что Y = 10; б) условный закон распределения У при условии, что Х = 6.

16. Непрерывная двумерная случайная величина (X, Y) распределена равномерно внутри прямоугольника с центром симметрии в начале координат и сторонами 2a и 2b, параллельными координатным осям. Найти: а) двумерную плотность вероятности системы; б) плотности распределения составляющих.

17. Заданы плотности распределения независимых составляющих непрерывной двумерной случайной величины (X, Y):

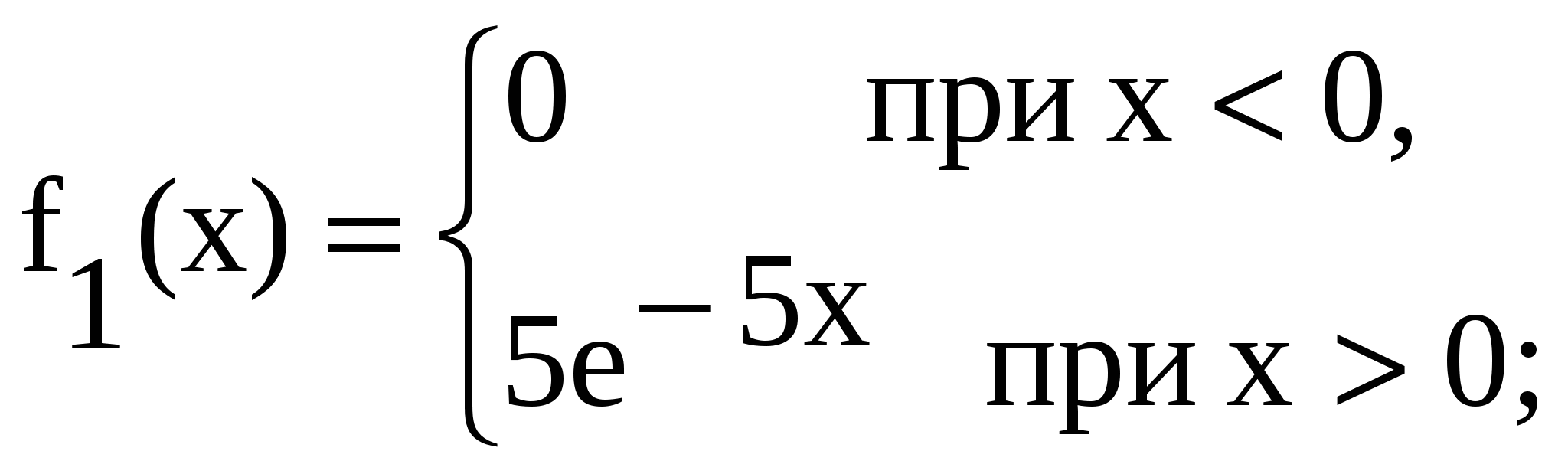
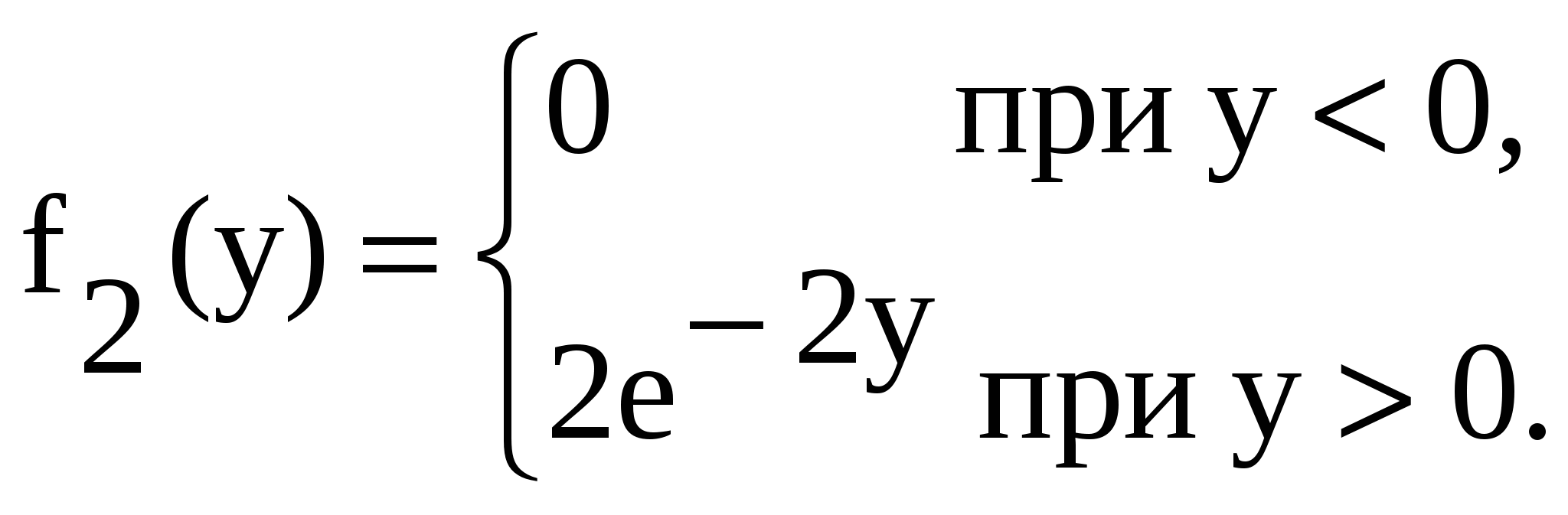
Найти: а) плотность совместного распределения системы; б) функцию распределения системы.