Прямая в пространстве. Виды уравнений прямой в пространстве

Взаимное ур-е 2-х прямых в пространстве: а) пусть прямые заданы своими канонич.ур-ями: x-x1/L1=y-y1/m1=z-z1/n1,

x-x2/L2=y-y2/m2=z-z2/n2; где `q 1(L1;m1;n1), `q2 (L2;m2;n2)- направляющие векторы. Тогда прямые параллельны, если параллельны их направляющие векторы:`q<sub>1</sub> úú`q₂ Þ L1/L2=m1/m2=n1/n2. б) пусть прямые заданы аналогично случаю а). Две прямые ^ тогда и только тогда, когда их направляющие векторы перпендикулярны (`q1^`q2).

L1L2+m1m2+n1n2=0. Существуют следующие виды ур-ий прямой в пространстве: 1)Общее ур-е прямой: прямая задаётся как линия пересечения 2-х плоскостей.

{A1x+B1y+C1z+D1=0

{A2x+B2y+C2z+D2=0, где А1, В1,С1-непропорциональные коэффициентам А2, В2, С2.

Эллипс есть геометрическое место точек, сумма расстояний которых от двух постоянных точек – фокусов эллипса – есть величина постоянная, равная 2а. Уравнение x²/a² + y²/b²=1определяющее эллипс в некоторой системе декартовых прямоугольных координат, есть уравнение второй степени; таким образом, эллипс есть линия второго порядка. Чтобы исследовать форму эллипса, выразим из уравнения y=+- Vb² (1-x²/a²) величину Y как функцию от Х. Оси симметрии эллипса называют обычно просто его осями, а точку пересечения осей—центром эллипса. Точки, в которых эллипс пересекает свои оси, называются его вершинами. Осями эллипса принято называть также отрезки АА'= 1а и ВВ' = 2b. Если эллипс расположен относительно координатных осей именно, если фокусы его находятся на оси Ох, то b=\/а² — с² => а > b. В этом случае отрезок ОА = называют (фокальной) большой полуосью эллипса, отрезок ОВ=b — малой полуосью.

Эллипсомназывается геометрическое место всех точек плоскости, сумма расстояний от которых до фокусов есть величина постоянная(2а), большая, чем расстояние между фокусами(2с).

Пусть М (х;у) – произвольная точка эллипса.

Т.к. MF₁ + MF₂ = 2a

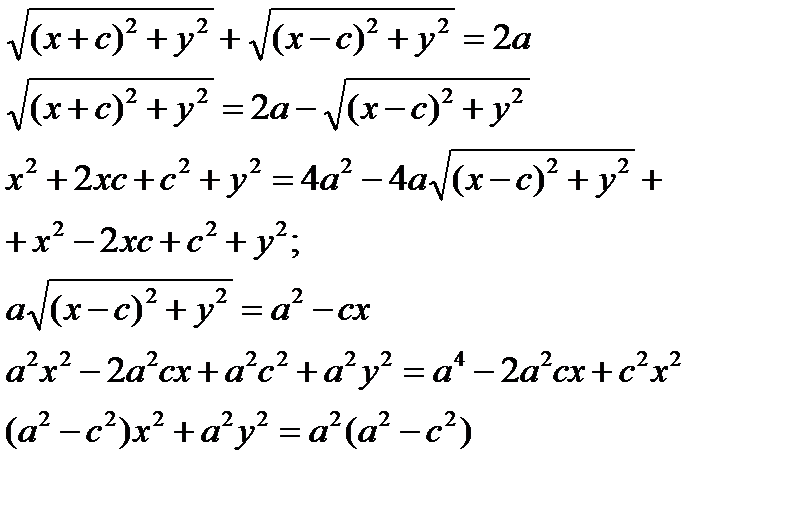
Т.к. 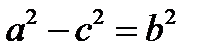То получаем 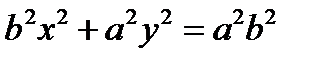или 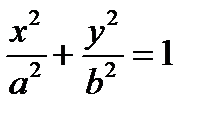- каноническое уравнение эллипса. Эксцентриситет-отношение длинны между фокусами к длине большой оси.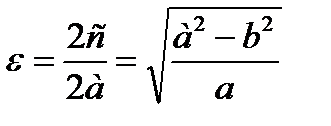

Если а<b то большая ось эллипса находится на оси y – ков (фокусы тоже) и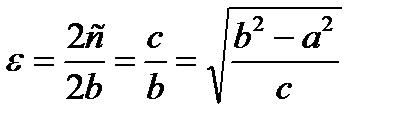

Гипербола геометрическое место точек, разность расстояний которых от двух постоянных точек – фокусов гиперболы – есть величина постоянная, равная 2а..

Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы |MF₁ – MF₂|=2a ур-е гиперболы: 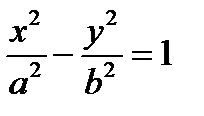расстояние от центра до любого фокусов: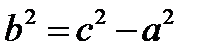

Множество точек плоскости удовлетворяющих уравнению гиперболы владеют следующими свойствами:

Модуль разности расстояний между точками, от каждой из которых до двух данных точек той же плоскости называемых фокусами есть величина постоянная (2a) и меньшая чем расстояние между фокусами (2с).

Эксцентриситет гиперболы находится по следующей формуле –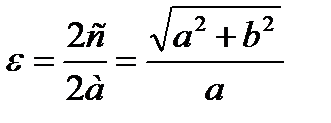

Если a=b то гипербола является равносторонней. Прямые у= ±в/а х называются асимптотами гиперболы.

М(х,у) – произвольные точки гиперболы, (х,у) – текущие координаты произвольной точки. Все точки гиперболы удовлетворяют условию

│F₁M-F₂M│=2a.

Парабола – множество всех точек плоскости, каждая из которых одинаково удалена от фокуса, и директрисы. Расстояние между фокусом и директрисой называется параметром параболы и обозначается через р>0.

Пусть M(x;y) – произвольная точка M с F. Проведем отрезок MN перпендикулярно

директрисе. Согласно определению MF=MN.

Каноническое уравнение параболы имеет вид:

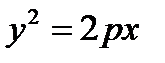
Каноническое уравнение параболы имеет два вида:

1) у²= 2рх – парабола симметрична относительно ох (рис.3)

2) х²= 2ру – парабола симметрична относительно оу (рис.4)

у

>

х

М(х,у)

F(p/2;0)

d

-р/2

М(х,у)

d

F(0,p/2)

х

у

-р/2

директриса

РИС.4

М (х,у) – произвольная точка парабола,

(х,у) – текущие координаты произвольной точки,

х = -р/2 – уравнение директрисы.

FM = d, где d – расстояние от точки М до директрисы.

В обоих случаях вершина параболы находится на оси симметрии в начале координат 0.

Парабола у² = 2рх имеет фокус F (р/2) и директрису х = - р/2

Парабола х = 2ру имеет фокус F (р/2) и директрису у = - р/2