Теплопроводность цилиндрической стенки

Рассматривается цилиндрическая стенка с внутренним тепловыделением q_v при отсутствии теплоотдачи с торцов. Температурное поле такой стенки описывается уравнением (3.23) с общим интегралом (3.26).

Рассмотрим случаи, когда теплоотдающей поверхностью являются:

1) наружная поверхность;

2) внутренняя поверхность;

3) обе поверхности.

Охлаждение только по наружной поверхности (рис. 3.4)

Дано: r₁ , r₂ , 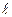, q_v, λ, t_{ж 2}, α₂.

Определить: уравнение температурного поля t=f(r), тепловой поток (Q₂, Вт), рассеиваемый наружной поверхностью.

Для нахождения постоянных интегрирования с₁ и с₂ в уравнении (3.26) потребуется два дополнительных условия: граничное условие третьего рода для наружной поверхности стенки

(3.31)

и условие максимума температуры на внутренней поверхности стенки

(3.32)

Решением системы уравнений (3.23), (3.31), (3.32) является уравнение температурного поля t=f(r) в виде

(3.33)

где r – текущий радиус.

Расчетные формулы для вычисления максимальной температуры (t_max), температуры наружной поверхности стенки (t_c2) можно получить, если в (3.33) подставить r=r₁, r=r₂ соответственно.

Тепловой поток, рассеиваемый наружной поверхностью стенки,

(3.34)

где V=p (r₂ ²- r₁ ²) 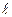, м³ – тепловыделяющий объем.

Охлаждение только по внутренней поверхности (рис. 3.5)

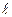Дано: r₁, _, r₂ . , q_v, λ, , .

Определить: t=f(r), Q₁, Вт.

Граничное условие третьего рода для внутренней поверхности стенки запишется в виде

(3.35)

Условие максимума температуры на наружной поверхности стенки

(3.36)

Решением системы уравнений (3.23), (3.35), (3.36) является уравнение температурного поля t=f(r)

(3.37)

Расчетные формулы для t_max и можно получить, если в (3.37) подставить r = r₂ и r= r₁ соответственно.

Тепловой поток Q₁,рассеиваемый внутренней поверхностью стенки, рассчитывается по уравнению (3.34).

Охлаждение по внутренней и наружной поверхностям (рис. 3.6)

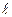Дано: r₁, _, r₂ . , q_v, λ, , .

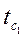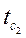Определить: t=f(r), радиус максимальной температуры r₀ , тепловые потоки Q₁ , Q₂.

Для нахождения постоянных интегрирования с₁ и с₂ в уравнении (3.26) и радиуса максимальной температуры r₀ потребуется три дополнительных условия: граничные условия первого рода на поверхностях стенки

при	(3.38)
при	(3.39)

и условие максимума температуры при r = r₀

(3.40)

Решением системы уравнений (3.23), (3.38) - (3.40) являются уравнение температурного поля стенки t=f(r)

(3.41)

где r – текущий радиус, и формула для расчета радиуса максимальной температуры

(3.42)

Формулы для расчета перепадов температуры в стенке получены на основании (3.41):

(3.43)

(3.44)

Потоки теплоты Q₁ и Q₂, рассеиваемые поверхностями стенки, рассчитываются по формулам

	(3.45)
	(3.46)

Суммарный тепловой поток

(3.47)

Контрольные задания

1. Рассчитайте объемную плотность внутреннего тепловыделения
(q_v, Вт/м³) стальной шины с размерами 3х100х1000 мм при допустимой нагрузке I=300A. Удельное электрическое сопротивление материала шины

Ответ: q_v=1,3×10⁵ Вт/м³.

2. Сделайте подстановку значения t_c в уравнение (3.10) и убедитесь, что правые части уравнений (3.10) и (3.11) одинаковы.

3. Запишите формулы для расчета температур 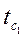и 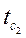на поверхностях пластины при несимметричных условиях ее охлаждения и граничных условиях третьего рода, используя уравнение температурного поля (3.15).

4. Запишите формулу для расчета максимальной температуры (t_max) пластины при несимметричных условиях охлаждения и граничных условиях первого рода, используя уравнение температурного поля (3.21).

5. Рассчитайте плотность внутреннего тепловыделения (q_v, Вт/м³), тепловой поток (Q, Вт), рассеиваемый поверхностью цилиндрического нихромового стержня диаметром d=5 мм, длиной 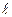=420 мм при напряжении U=10В и электрическом сопротивлении R=0,025 Ом.

Ответы: q_v=4,83×10⁸ Вт/м³; Q=N=4000 Вт.

6. Для цилиндрической стенки с охлаждением только по наружной поверхности, используя уравнение температурного поля (3.33), получите расчетные формулы для t_max , 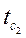, t_max - .

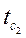7. Для цилиндрической стенки с охлаждением только по внутренней поверхности, используя уравнение температурного поля (3.37), получите расчетные формулы для t_max , 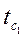, t_max - .

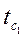8. Сделайте вывод формул (3.43) и (3.44), и убедитесь в их правильности.