Глава 3. фундаментальная теорема покера

В алгебре и дифференциальном исчислении есть свои основные (фундаментальные) теоремы. Настало время ввести Фундаментальную Теорему покера. Покер, как и все карточные игры, - это игра с неполной информацией, что отличает ее от таких настольных игр как шахматы, шашки и нарды, где вы всегда можете видеть, что делает ваш оппонент. Если бы все карты были открыты все время, каждый игрок мог бы играть точно и математически грамотно. Любой отклоняющийся от правильной игры уменьшает свое математическое ожидание и увеличивает его у соседей.

Конечно, если бы все карты были открыты все время, не было бы такой игры, как покер. Искусство покера состоит в восстановлении неполной информации, получаемой от торговли игроков и светлых карт в полуоткрытых типах игры; в то же время вы должны препятствовать вашим оппонентам узнать больше, чем вы бы желали, чтобы они знали, о вашей руке.

Это ведёт вас к фундаментальной Теореме покера:

Всякий раз, когда вы разыгрываете комбинацию отлично от того, как вы бы играли, если бы видели карты всех ваших противников, они выигрывают; и всякий раз, когда вы разыгрываете комбинацию так, как поступили бы, видя все их карты, они проигрывают. И наоборот: всякий раз, когда оппоненты разыгрывают свои комбинации отлично от того, как они бы это сделали, видя все ваши карты, вы выигрываете; и всякий раз, когда они разыгрывают руки таким же образом, как если бы видели все ваши карты, вы проигрываете.

Фундаментальная Теорема действует всецело, когда игра сокращается к поединку между вами и вашим единственным противником. Также она почти всегда применима к игре с более чем двумя участниками, за редкими исключениями, которые будут обсуждаться в конце главы.

Что означает Фундаментальная Теорема? Представьте, что если бы каким-то образом оппонент узнал вашу руку, он бы играл совершенно точно. Например, если бы в покере с заменой карт противник увидел, что у вас завершённый флеш ещё до обмена, совершенно правильно на его месте было бы выбросить пару тузов после вашей ставки. Ответить было бы ошибкой, но это особого рода ошибка. Мы не имеем в виду, что оппонент играл плохо, ответив с парой тузов; мы хотим сказать, он сыграл эту руку отлично от того, как если бы видел ваши карты.

Этот пример с флешем весьма очевиден. Фактически вся Теорема прозрачна, в чем и состоит ее красота; однако ее применения зачастую не так очевидны. Иногда количество денег в банке заставляет вас принять ставку, даже если вы смогли увидеть, что рука противника лучше вашей. Давайте рассмотрим несколько примеров Фундаментальной Теоремы Покера в действии.

ПРИМЕРЫ ФУНДАМЕНТАЛЬНОЙ ТЕОРЕМЫ ПОКЕРА

Пример 1

Предположим, когда вы делаете ставку, ваша рука не так хороша, как у оппонента. Он принимает ее, и вы проигрываете. Но на самом деле вы не проиграли - вы выиграли! Почему? Потому что очевидно, правильной тактикой оппонента, если бы он знал, что у вас, было бы поднять ставку. Следовательно, вы выиграли, если он ее не поднял, а если он скидывает карты, вы выигрываете огромное количество денег.

Данный пример может показаться слишком очевиден для серьезного обсуждения, но это типичная ситуация даже в некоторых довольно сложных играх. Положим, в безлимитном холдеме у вас

а у противника разномастный марьяж

В прикупе (первые три открытые карты которого носят название флоп) приходят

Вы пасуете, противник ставит, и вы принимаете его ставку. Четвёртой картой приходит туз бубен, и вы делаете ставку, пытаясь показать, что у вас тузы. Если бы оппонент знал, что у вас, ему следовало бы поднять вас настолько, что было бы слишком дорого дотягивать до флеша или стрита на последней карте, и вам пришлось бы сдаться. Следовательно, если оппонент только уравнивает ставку, вы выиграли. Вы выиграли не просто потому, что получили сравнительно дешевую последнюю карту, а потому, что оппонент неправильно играл. Очевидно, если противник сдаётся, вы очень здорово заработали, поскольку он выкинул лучшую руку.

Пример 2

Предположим, в банке $80, и у вас две пары. Вы играете в покер с обменом и ставите $10, которые, будем считать, все, что вы можете поставить. У вашего единственного оппонента флеш-дро,то есть, флеш на четырёх картах - одной не хватает. Вопрос: вы хотите, чтобы он ответил или скинул карты? Естественно, вы хотите, чтобы он поступил так, как наиболее выгодно вам. Фундаментальная Теорема Покера утверждает, что для вас наиболее выгодно, чтобы партнёр сыграл неточно, основываясь на неполной информации об обеих руках. Поскольку шансы противника с банка 9 к 1 (его $10 могут принести ему $90), а вероятность поймать флеш 5 к 1, для него правильно принять ставку, поскольку тогда он получает положительное матожидание. Ну и раз для него правильно принять ставку, следуя Фундаментальной Теореме Покера, для вас выгодно, чтобы он сбросил карты.

Такого рода ситуация бывает часто. У вас лучшая рука, а у оппонента достаточно хорошие шансы, что делает правильным для него принятие ставки, если бы он знал, что у вас. Следовательно, вы хотите, чтобы оппонент скинулся. К тому же для вас правильно продлить игру, раз у вас достаточные шансы взять банк. Если же вы не продлеваете ее, то просто выкидываете деньги и даёте выиграть вашему противнику.

Пример 3

Поскольку вашему оппоненту резонно поддерживать игру, когда он имеет достаточные шансы взять банк, вы можете иногда подсобить ему неправильно скинуться, демонстрируя больше силы в руке, чем это есть на самом деле, на первых кругах торговли. Предположим, в семикарточном стад-покере вы делаете ставку, имея на руке закрытые

Оппонент поддерживает вашу ставку с такими картами: две закрытых и открытые

Вы вполне уверены, что у него пара королей. Теперь с прикупом у вас получается пара шестерок в светлую, и вы ставите. Противник почти наверняка сбросит свою пару королей, поскольку он боится, что вы накопили две пары, из которых старшая - тузы.

Некоторые могут сказать: «Хорошо, подождите секундочку. Почему я не хочу, чтобы оппонент принял ставку, - ведь его пара королей хуже, чем мои две небольшие пары?» Ответ таков, что если придут ещё карты, и оппонент получит хорошую возможность победы, лучше выиграть банк прямо сейчас. При паре королей против двух мелких пар только очень хорошие шансы могут оправдать принятие ставки. Поскольку правильным для оппонента было бы принять ставку, вы выиграете, если заставите его скинуться.

Пример 4

В раззе, то есть семикарточном стад-лоуболле, где выигрывает нижайшая комбинация, мы находим ещё один пример того, что иногда неплохо показать больше силы, чем есть на самом деле, чтобы заставить игрока не вовремя скинуться. Положим, у вашего противника две закрытые, три открытые карты

а у вас что-то типа

Если вы думаете, что у оппонента лоу на четырёх от 8, а у вас пара и неполный лоу на четырёх от 7-8, необходимо сделать ставку, даже если вы знаете, что будет ответ. Ставка даст вам дополнительные шансы, например, возможно, вам придёт мелочь на шестой карте, и получится лоу от 7-8. Если оппонент возьмёт большую карту или пару плюс у него остается вариант наменять лучший стрит от 8, чем ваш, он всё равно сбросит карты, поскольку ваша предыдущая ставка показывала, что у вас уже набран лоу от 8. Мелкая карта, которую вы сейчас вытянули, говорит о том, что у вас уже есть нижний 7-лоу, а это заставляет оппонента думать, что он потянет «мёртвую карту», не имея никаких шансов на выигрышную комбинацию.

Заметьте, что опять вы хотите заставить оппонента скинуться, несмотря на то, что у вас лучшая рука. У вас лоу от 7,8, и вы тянете к 7, хотя все, что может сделать ваш оппонент, это улучшить лоу от 8. Однако вы выигрываете, если он скинется, поскольку если бы он знал, что у вас на руках всего 7,8, у него были нормальные шансы поставить ставку в надежде «перетянуть» вас в процессе обмена. Не поставив, он сделал ошибку, и вы выиграли. (Вы выигрываете даже больше, когда на шестой карте у вас образуется две пары, и ваш противник выходит из игры на лучшей руке.)

Пример 5

Так же как вы стремитесь, чтобы оппонент вышел из игры, когда у него достаточные шансы взять банк, так вы стараетесь, чтобы он заявил ставку, имея недостаточные шансы взять банк. Так, часто бывает правильно сыграть слабо на сильной руке в первых кругах торговли - обратное тактике предыдущих двух примеров, с тем, чтобы ваш оппонент не вовремя уровнялся, когда вы улучшите комбинацию. Посмотрим на следующие две руки в семикарточном раззе.

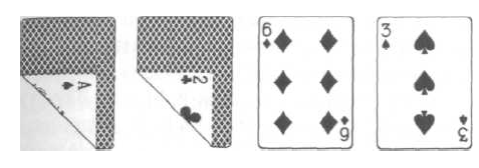
Вы:

Оппонент:

Хорошей тактикой с такой рукой против некоторых игроков было бы спасовать и уравняться, если ваш оппонент делает ставку. Многие игроки имеют пару или плохую карту закрытую. Если вы прикупите в светлую 4, 5 или 7, что даст вам лоу от 6 или 7, ваш оппонент, вероятно, всё равно сделает ставку, даже если он тянет вмёртвую, потому что прежние ваши ходы в совокупности с его шансами взять банк заставляют его думать, что стоит ставить. А это как раз то, на что вы надеетесь. Ваши обманчивые ходы в начале партии заставили вашего оппонента неправильно сыграть на последних кругах.

Пример 6

Всякий раз, когда у противника неважные шансы против вас, вы заставляете его уравняться, даже если, уравнявшись, он получает шанс произвести обмен лучше вас. Если бы в примере с флешем в начале этой главы банк составлял $20, а не $80, вы бы хотели, чтобы оппонент с флешем на четырёх уравнял вашу $10 ставку, поскольку шансы завершения комбинации у него составляют 5 к 1, а получает он денег только 3 к 1. Если он уравнивается и набирает флеш, значит такова судьба. Тем не менее, его игра неправильна, поскольку она имеет отрицательное матожидание, и вы потенциально выигрываете всякий раз, когда он так поступает.

Если у вас такие карты, на которых вы хотите, чтоб вам ответили, не заставляйте оппонента скинуться, поставив невероятное количество денег в беспредельной игре или в покере с лимитированным банком. Такая ситуация возникла однажды, когда я играл в безлимитный холдем. Оставалось получить всего одну карту, у меня сидел стрит, который на тот момент был просто блеск или nuts - наилучшая возможная рука. Я поставил что-то типа $50, партнёр слева поддержал, а игрок после него уравнялся «полтинником» ($50) и поднял ставку на столько, сколько было у него денег, то есть примерно на $200.

Поскольку у меня была лучшая возможная рука, вопрос стоял так: поднимать ставку или просто уравняться? В банке было что-то около $500. Поскольку третий выложил все, что имел, я должен был думать только об игроке после меня. Я знал, что подниму я, скажем, на $400, что составит него $600, он непременно уйдет; на самом деле, если бы я поднял сейчас ставку практически на любую сумму, он бы «ушел» (скинулся). Но если б я просто ответил $200, он, возможно бы, уравнялся.

Что я желал от него? Я был совершенно уверен, что у него две пары. Если бы я ответил $200, в банке стало бы около $700, что обеспечивало ему шансы с банка 7 к 2, чтобы уравняться $200 со своими двумя парами. Однако шансы против того, что он с двумя парами наберёт фулл-хаус, были 10 к 1 (в колоде оставалось 40 ненужных ему карт и 4 нужных). Следовательно, если бы он знал, что у меня стрит, ему было бы нерезонно рассчитывать на 7 к 2 при шансах набрать комбинацию 1 к 10. Поэтому я просто ответил $200, и, как я полагал и надеялся, он сделал то же самое.

Грустный итог моего повествования состоит в том, что он набрал фулл-хаус, добавив совсем небольшую сумму, которую я оплатил. Многие считали, что я был неправ, позволив ему играть дальше вместо того, чтобы заторговать, но на самом деле это они неправы. Я должен был дать ему шанс сделать ошибку, которую он и сделал, поскольку как только мой противник ошибается, я выигрываю на длинной дистанции.

«ОШИБКИ» ПО ФУНДАМЕНТАЛЬНОЙ ТЕОРЕМЕ ПОКЕРА

Очень важно понимать, что когда мы говорим об ошибках в соответствии с Фундаментальной Теоремой Покера, мы не обязательно имеем в виду плохую игру. Мы говорим об очень странном виде ошибок - ходах, отличных от тех, которые бы вы сделали, видя все карты ваших партнёров. Если у меня флеш-рояль (от туза), а у кого-то стрит-флеш от короля, значит, он делает ошибку, уравниваясь со мной. Но, конечно же, нельзя винить партнёра в плохой игре, если он отвечает или, что гораздо более вероятно, поднимает ставку, имея на руках стрит-флеш от короля. Он не знает, что у меня, поэтому он делает ошибку в другом смысле слова.

В игре с продвинутыми игроками вы постоянно пытаетесь заставить их делать то, что неправильно, судя по вашей карте. Всякий раз, когда они играют правильно в соответствии с тем, что у вас на руках, вы проигрываете. Если вспомнить Фундаментальную Теорему Покера, вы играете на выигрыш, если ходите как можно ближе к тому, как будто видите карты всех ваших партнёров; и надо постараться заставить ваших оппонентов играть как можно дальше от этого идеально-утопического уровня. Первая цель достигается в основном за счёт точного чтения рук и мыслей партнёров, поскольку, чем ближе вы подойдете к отгадке чужих комбинаций, тем меньше вы сделаете ошибок в соответствии с Фундаментальной Теоремой. Вторая цель достигается за счёт обманной игры.