Линейные однородные уравнения высших порядков

Всё очень и очень похоже.

Линейное однородное уравнение третьего порядка имеет следующий вид:
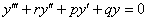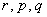, где – константы.
Для данного уравнения тоже нужно составить характеристическое уравнение и найти его корни. Характеристическое уравнение, как многие догадались, выглядит так:
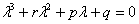, и оно в любом случае имеет ровно три корня.

Пусть, например, все корни действительны и различны: 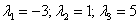, тогда общее решение запишется следующим образом:

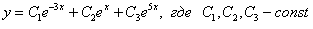
Если один корень действительный 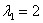, а два других – сопряженные комплексные 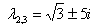, то общее решение записываем так:

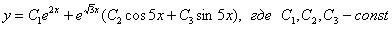
Особый случай, когда все три корня кратны (одинаковы). Рассмотрим простейшие однородное ДУ 3-го порядка с одиноким папашей: 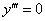. Характеристическое уравнение 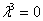имеет три совпавших нулевых корня 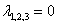. Общее решение записываем так:

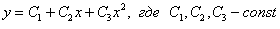
Если характеристическое уравнение 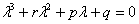имеет, например, три кратных корня 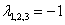, то общее решение, соответственно, такое:

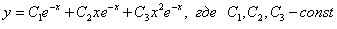
Пример 9

Решить однородное дифференциальное уравнение третьего порядка

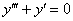
Решение: Составим и решим характеристическое уравнение:

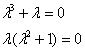
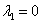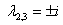, – получен один действительный корень и два сопряженных комплексных корня.

Ответ: общее решение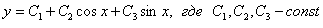

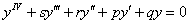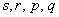Аналогично можно рассмотреть линейное однородное уравнение четвертого порядка с постоянными коэффициентами: , где – константы.

Соответствующее характеристическое уравнение 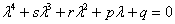всегда имеет ровно четыре корня.

Общее решение записывается точно по таким же принципам, как и для однородных диффуров младших порядков. Единственное, хотелось прокомментировать тот случай, когда все 4 корня являются кратными. Пусть, например, характеристическое уравнение имеет четыре одинаковых корня 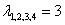. Тогда общее решение записывается так:
.

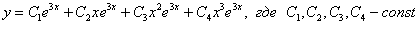Тривиальное уравнение 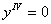имеет общее решение:

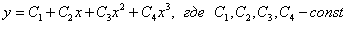
Пример 10

Решить однородное дифференциальное уравнение четвертого порядка

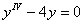
Это пример для самостоятельного решения, полное решение и ответ в конце урока.

Полагаю, практически все смогут расправиться и с однородными дифференциальными уравнениями 5-го, 6-го и высших порядков. Мне очень не хотелось записывать общие формулы, рассказывать о фундаментальной системе решений и т.д. Но, процесс конструирования общего решения вроде раскрыт мной неплохо.

На посошок предлагаю решить однородный диффур как раз для закрепления вашего понимания. Да чего мелочиться:

Пример 11

Решить однородное дифференциальное уравнение шестого порядка

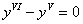
Полное решение и ответ ближе к подвалу. Караул устал – караул упал.

После такой основательной подготовки можно смело переходить к освоению линейных неоднородных уравнений второго и высших порядков.

Желаю успехов!

Решения и ответы:

Пример 2: Решение: Составим и решим характеристическое уравнение:

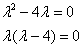
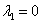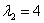, – различные действительные корни
Ответ: общее решение: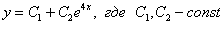
Проверка: Найдем производную:

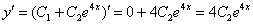
Найдем вторую производную:

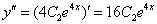
Подставим 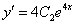и 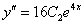в левую часть исходного уравнения :
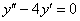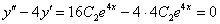, таким образом, общее решение найдено правильно.

Пример 4: Решение: составим и решим характеристическое уравнение:


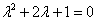
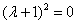
Получены два кратных действительных корня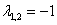
Ответ: общее решение: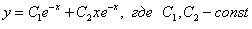

Пример 6: Решение: Составим и решим характеристическое уравнение:


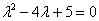
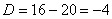
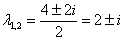– сопряженные комплексные корни
Ответ: общее решение: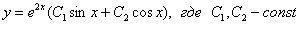

Пример 8: Решение: Составим и решим характеристическое уравнение:

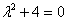
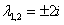– получены сопряженные комплексные корни, поэтому общее решение:

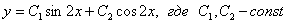
Найдем частное решение, удовлетворяющее заданным начальным условиям:
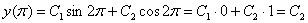, то есть 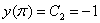, (значение константы получилось сразу же).

.
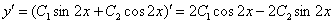
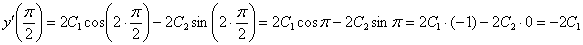То есть .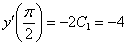
Составим и решим систему:

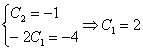
Ответ: частное решение: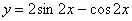
Проверка: 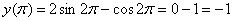– начальное условие выполнено.

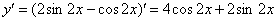
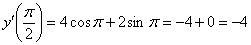– второе начальное условие выполнено.

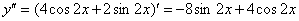
Подставим 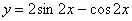и 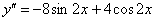в левую часть исходного уравнения:

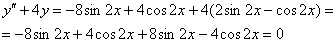
Получена правая часть исходного уравнения (ноль).
Такие образом, здание выполнено верно.

Пример 10: Решение: Составим и решим характеристическое уравнение:

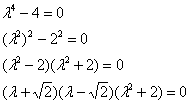
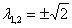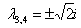, – получены два различных действительных корня и два сопряженных комплексных корня.
Ответ: общее решение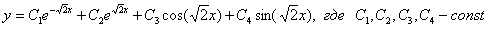

Пример 11: Решение: Составим и решим характеристическое уравнение:

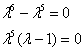
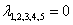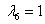, – получены пять кратных нулевых корней и действительный корень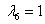
Ответ: общее решение

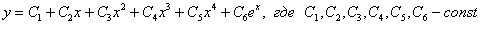
Как решить неоднородное дифференциальное уравнение
второго порядка?

Данная статья является логическим продолжением урока Однородные уравнения второго и высших порядков. Как я уже отмечал, для того чтобы научиться решать неоднородные уравнения вида 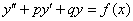, необходимо уверенно щёлкать более простые однородные диффуры вида 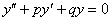. Впрочем, они доступны даже для школьника, поскольку для решения однородного уравнения 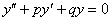требуется лишь правильно решить обычное квадратное уравнение, которое проходят, вроде, в 8-ом классе. Предполагаю, что вы уверенно расправляетесь с однородными уравнениями, если это не так, пожалуйста, посетите предыдущий урок.

Неоднородные уравнения – это просто!

А самых прилежных читателей в конце урока ждёт морковка подарок от Дедушки Мороза!

Как решить линейное неоднородное уравнение с постоянными коэффициентами вида ?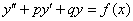

Алгоритм решения неоднородного ДУ следующий:

1) Сначала нужно найти общее решение соответствующего однородного уравнения. Да-да, взять уравнение 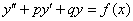, откинуть правую часть: 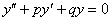– и найти общее решение. Данная задача подробно разобрана на уроке Однородные уравнения второго и высших порядков. Общее решение однородного уравнения я привык обозначать буквой .

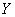2) Наиболее трудный этап. Необходимо найти какое-либо частное решение 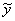неоднородного уравнения. Сделать это можно так называемым способом подбора частного решения с применением метода неопределенных коэффициентов.

Внимание! Для освоения метода подбора будет жизненно необходим методический материал Как подобрать частное решение неоднородного уравнения? Данную справку лучше по возможности распечатать, очень удобно, если она будет перед глазами. Но не спешите вникать в эти таблицы, если являетесь чайником! Всему свое время.

3) На третьем этапе надо составить общее решение 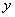неоднородного уравнения. Это совсем легко: 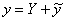. Совершенно верно – следует просто приплюсовать завоёванные трофеи.

Если изначально в условии сформулирована задача Коши (найти частное решение, удовлетворяющее заданным начальным условиям), то добавляется четвёртый этап:

4) Нахождение частного решения, удовлетворяющего заданным начальным условиям. Порядок нахождения частного решение для уравнения второго порядка уже немного рассмотрен на уроке Однородные уравнения второго и высших порядков. В случае с неоднородным диффуром принципы нахождения частного решения сохраняются.

Примечание: В ваших лекциях, практических занятиях общее решение однородного уравнения 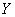и подобранное частное решение неоднородного уравнения 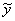, скорее всего, обозначаются не так. Я «намертво» привык к обозначениям 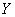, 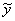и буду использовать именно их.

Не так всё страшно, переходим к практическим задачам.

Пример 1

Найти общее решение дифференциального уравнения.

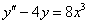
Решение:
1)Сначала найдем общее решение соответствующего однородного уравнения. Берём наш неоднородный диффур 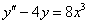и обнуляем правую часть:

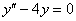
Составим и решим характеристическое уравнение:

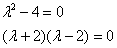
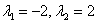– получены различные действительные корни, поэтому общее решение: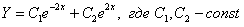

2) Теперь нужно найти какое-либо частное решение 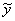неоднородного уравнения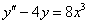

И вопрос, который вызывает затруднения чаще всего: В каком виде нужно искать частное решение ?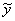

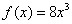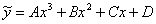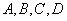Прежде всего, смотрим на нашу правую часть: . Тут у нас многочлен третьей степени. По идее, частное решение тоже следует искать в виде многочлена третьей степени: , где – пока ещё неизвестные коэффициенты (числа). Образно говоря, нужно посмотреть на правую часть неоднородного уравнения и «собезьянничать» её, но уже с неопределёнными коэффициентами. Вариант подбора, который «сразу приходит в голову», я неформально буду называть обычным, обыкновенным или штатным случаем.

После предварительного анализа смотрим на корни характеристического уравнения 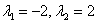, найденные на предыдущем этапе: это различные действительные корни, отличные от нуля. В методическом материале Как подобрать частное решение неоднородного уравнения? данному случаю соответствует Раздел I. Анализируя примеры №№1-4 справки, приходим к выводу, что, да, действительно – частное решение неоднородного уравнения нужно искать в виде:

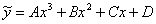
После правильно выбранного подбора алгоритм пойдёт по накатанной колее. Используем метод неопределенных коэффициентов. Кто не знаком – узнает.

Найдём первую и вторую производную:

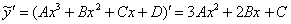
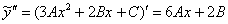
Подставим 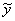и 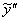в левую часть неоднородного уравнения:

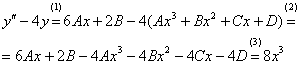
(1) Выполняем подстановку 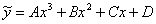и .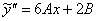
(2) Раскрываем скобки.
(3) После максимальных упрощений ставим знак равенства и приписываем нашу правую часть .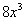

Далее работаем с последним равенством – необходимо приравнять коэффициенты при соответствующих степенях и составить систему линейных уравнений. В картинках процесс выглядит так:

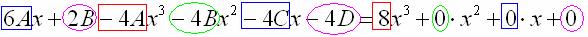
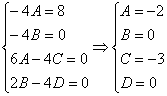
Чтобы было еще проще, новичкам рекомендую предварительно сгруппировать подобные слагаемые:
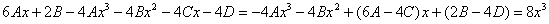, и только потом составлять систему.

В данном случае система получилась очень простой, и многие из читателей справятся с ней даже устно.

Подставляем найденные значения 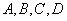в наш исходный подбор частного решения :

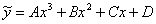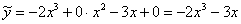
Таким образом, подобранное частное решение неоднородного уравнения:

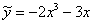
3) Запишем общее решение неоднородного уравнения:

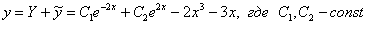
Всё!

Ответ: общее решение: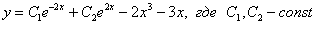

Для неоднородных уравнений второго порядка я люблю проводить проверку-«лайт». Сначала я проверяю, правильно ли решил квадратное уравнение. После такой проверки первая часть ответа 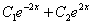(общее решение однородного уравнения) будет гарантировано правильной.

Осталось проверить, верно ли найдена вторая часть ответа (подобранное частное решение): 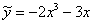. Это тоже довольно просто.
Найдем первую и вторую производную:

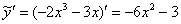
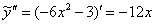
Подставим 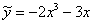и 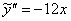в левую часть неоднородного уравнения:
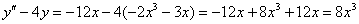– получена правая часть исходного уравнения, значит, частное решение 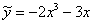найдено правильно.

Существует и полный вариант проверки, о нём речь пойдет, когда я разберу задачу Коши.

Пример 2

Найти общее решение дифференциального уравнения.

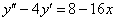
Выполнить проверку-«лайт». Это пример для самостоятельного решения, полное решение и ответ в конце урока.

Будьте внимательны, пример «с подвохом»!

А поэтому повторим, по какой схеме подбирать частное решение:
– Смотрим на правую часть 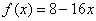и подбираем первоначальный «штатный» вид частного решения .
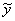– Смотрим на корни характеристического уравнения и в справке Как подобрать частное решение неоднородного уравнения? находим нужный раздел (всего их там пять).
– Знакомимся с разделом и уточняем, в каком же виде нужно искать частное решение .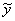

Пример 3

Найти общее решение неоднородного дифференциального уравнения.

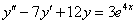
Решение:
1) Найдем общее решение соответствующего однородного уравнения:

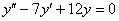
Составим и решим характеристическое уравнение:



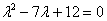
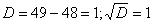
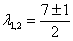
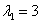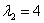, – получены различные действительные корни, среди которых нет нуля, поэтому общее решение: .

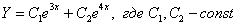2) Выясняем, в каком виде нужно искать частное решение ?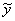

Сначала смотрим на правую часть и выдвигаем первую гипотезу: раз в правой части находится экспонента, умноженная на константу 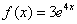, то частное решение, по идее, нужно искать в виде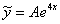

Далее смотрим на корни характеристического уравнения 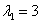, , 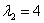найденные в предыдущем пункте. Это два действительных корня, среди которых нет нуля. Данному случаю соответствует Раздел I справочного материала. Изучив примеры 5-8 таблицы, приходим к выводу, что наш первоначальный вариант подбора необходимо домножить на «икс». То есть, частное решение дифференциального уравнения следует искать в виде:
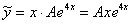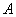, где – пока еще неизвестный коэффициент, который предстоит найти.

После того, как подобран корректный вид частного решения, алгоритм работает стандартно, единственное, вы должны уметь уверенно находить производные, в частности, использовать правило дифференцирования произведения 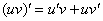. В ходе вычислений я не буду подробно расписывать производные.

Найдем первую и вторую производную:

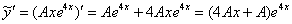
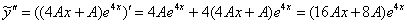
Подставим 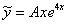, 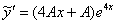и 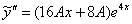в левую часть неоднородного уравнения:

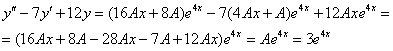
Что сделано? Подстановка, упрощение, сокращение, и в конце – приравнивание к исходной правой части .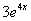

Здесь повезло: из последнего равенства 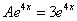автоматически получаем .
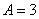Найденное значение 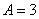подставляем в наш исходный подбор .

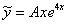Таким образом, частное решение: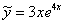

3) Составляем общее решение неоднородного уравнения:

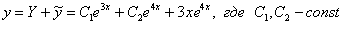
Ответ: общее решение: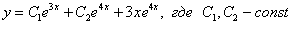

Подчеркиваю, что всегда полезно выполнить «быструю» проверку, проверив, по крайне мере, подобранное частное решение .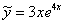

Думаю, что после трёх разобранных примеров вы уже понимаете, как и на каком этапе надо использовать справочный материал Как подобрать частное решение неоднородного уравнения? Теперь всем читателям, в том числе чайникам, рекомендую прочитать справку полностью.

Что произойдет, если мы неправильно подберём вид частного решения? Вот в только что разобранном примере мы искали частное решение в виде 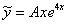, а что будет, если попробовать искать частное решение в виде 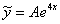или в каком-то другом виде? Поначалу всё будет хорошо: удастся найти производные 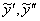, провести подстановку. Но далее перед глазами возникнет грустный факт: у нас не получится красивого финального равенства 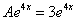, грубо говоря, «ничего не сойдётся»:




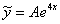
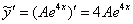
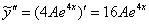
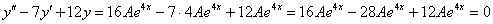
Сократилось вообще ВСЁ! Совершенно очевидно, что в конце нельзя приписать правую часть 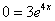, хотя бы потому, что 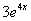не может равняться нулю.

Для закрепления материала пара примеров для самостоятельного решения:

Пример 4

Найти общее решение неоднородного дифференциального уравнения.

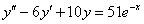
Пример 5

Найти общее решение неоднородного дифференциального уравнения.

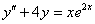
Полные решения и ответы в конце урока.

Коши шепчет, что пора рассмотреть его задачу.

Пример 6

Найти частное решение неоднородного уравнения, соответствующее заданным начальным условиям.
, ,

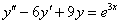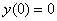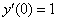
Алгоритм решения полностью сохраняется, но в конце добавляется дополнительный пункт.

Решение:
1) Найдем общее решение соответствующего однородного уравнения:

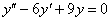
Характеристическое уравнение:


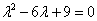
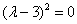
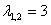– получены кратные действительные корни, поэтому общее решение:

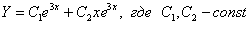
2) Выясняем, в каком виде нужно искать частное решение 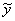. Смотрим на правую часть неоднородного уравнения 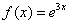, и сразу появляется первая версия подбора: .

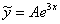Далее смотрим на корни характеристического уравнения: 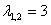– действительные кратные корни. Изучая Раздел III, примеры 24-26 справочных материалов, приходим к выводу, что «очевидное» частное решение 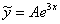необходимо домножить на 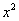, то есть, частное решение следует искать в виде:

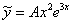
Ищем неизвестный коэффициент .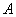

Найдем первую и вторую производную:

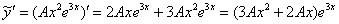
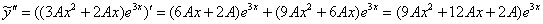
Подставим 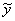, 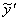и 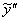в левую часть неоднородного уравнения и максимально упростим выражение:

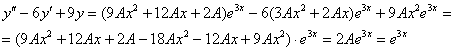
В самом конце после упрощений приписываем исходную правую часть .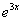

Из последнего равенства 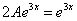следует:

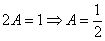
Таким образом: .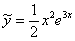

3) Составим общее решение неоднородного уравнения:

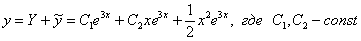
4) Найдем частное решение, удовлетворяющее заданным начальным условиям ,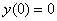

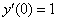
Как уже отмечалось, порядок нахождения частного решения немного рассматривался на уроке Однородные уравнения второго и высших порядков. Повторим.

Сначала берём найденное общее решение 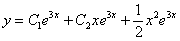и применяем к нему первое начальное условие :

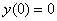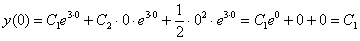
Согласно начальному условию: 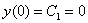– получаем первое уравнение.

Далее находим производную от общего решения:
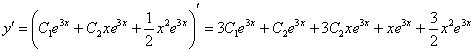и применяем к найденной производной второе начальное уравнение :

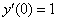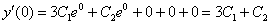
Согласно второму начальному условию: 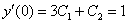– получаем второе уравнение.

Составим и решим систему:

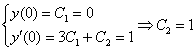
Подставим найденные значения констант 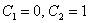, в общее решение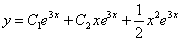

Ответ: частное решение: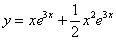

Выполним полную проверку:

Сначала проверяем, выполняется ли начальное условие :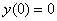
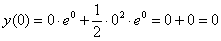– да, начальное условие выполнено.

Находим производную от ответа:

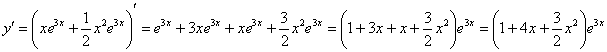
Проверяем, выполняется ли второе начальное условие :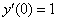
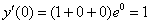– да, второе начальное условие тоже выполнено.

Берём вторую производную:

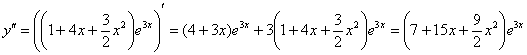
Подставим найденное частное решение 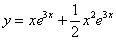и его производные 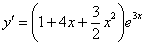, 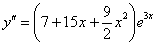в левую часть исходного уравнения:

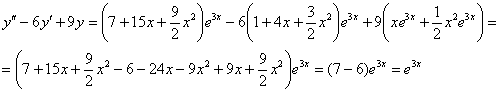
Получена правая часть исходного уравнения, значит, задание выполнено правильно.

Аналогично можно выполнить полную проверку любого общего решения с той лишь разницей, что не нужно проверять выполнение начальных условий.

Что важно? Важно уметь хорошо дифференцировать и быть внимательным.

Пример 7

Найти частное решение неоднородного уравнения, соответствующее заданным начальным условиям.
, ,
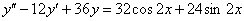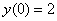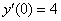
Выполнить полную проверку.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

И еще пара примеров, что-то синусов с косинусами маловато было.

Пример 8

Найти общее решение неоднородного уравнения

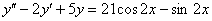
Решение:
1)Найдем общее решение соответствующего однородного уравнения:

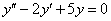
Характеристическое уравнение:



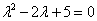
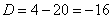
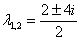
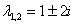– получены сопряженные комплексные корни, поэтому общее решение:
.

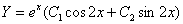2) Частное решение неоднородного уравнения ищем в «обычном» виде: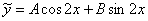
(при подборе не забываем посмотреть Раздел IV справочной таблицы).

Выясним, чему равны коэффициенты .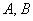

Найдем производные:

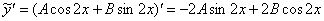
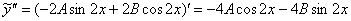
Подставим 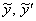и 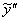в левую часть неоднородного уравнения:

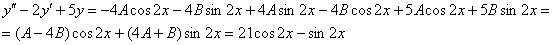
(После подстановки и максимальных упрощений приписываем правую часть: )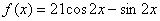

Из последнего равенства 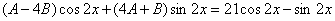составим и решим систему:

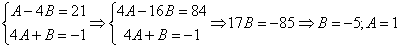
Здесь первое уравнение умножено на 4, а затем проведено почленное вычитание: из второго уравнения я почленно вычел первое уравнение. Если метод не знаком или позабылся, смотрите урок Как решить систему линейных уравнений? Естественно, при решении системы не возбраняется применять «школьный» метод подстановки, другое дело, что в похожей ситуации это обычно не очень выгодно и удобно.

Таким образом, подобранное частное решение: .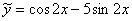

3) Составим общее решение неоднородного уравнения:

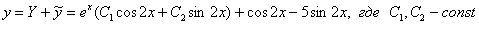
Ответ: общее решение: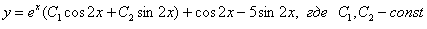

Пример 9

Найти общее решение неоднородного уравнения

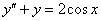
Это пример для самостоятельного решения. Будьте внимательны при подборе частного решения 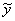! Полное решение и ответ в конце урока.

В конце урока обещанные новогодние подарки. Что в новогодние праздники приносит Дедушка Мороз студентам? На этот вопрос ответ знаю только я. В Новый год Дедушка Мороз принесёт вам большой мешок неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами. У меня их много.

На самом деле очень хотелось рассмотреть и другие диффуры, но таки статья должна укладываться в разумные размеры, чтобы Коши действительно не зашептал не обиделись поисковики, Яшенька, бедный, и так у нас очень глючный. Поэтому предлагаю для самостоятельного решения еще несколько уравнений, которые показались мне интересными, но не вошли в «основную сетку» урока.

Для следующих примеров полного решения не будет, будут только готовые ответы в конце урока. Но, даже из одних ответов вы сможете «вытащить» информацию, например, в каком же виде надо выполнить подбор частного решения. Среди предлагаемых ДУ есть как несложные диффуры, так и уравнения повышенной сложности.

Придерживайтесь алгоритма, будьте внимательны и успешного вам дифференцирования!

Пример 10

Найти общее решение неоднородного уравнения

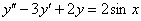
Пример 11

Найти общее решение неоднородного уравнения

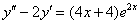
Пример 12

Найти частное решение неоднородного уравнения, соответствующее заданным начальным условиям.
, ,

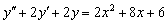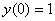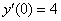
Пример 13

Найти частное решение неоднородного уравнения, соответствующее заданным начальным условиям.
, ,

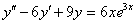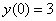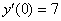
Пример 14

Найти общее решение неоднородного уравнения

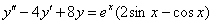
Пример 15

Найти общее решение неоднородного уравнения

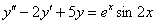
Должен сказать, что примеры №№13-15 достаточно сложны в техническом плане, при подборе частного решения появляются громоздкие производные, которые еще и нужно подставлять в левую часть уравнения. Но, как оптимист, предполагаю, что данные уравнения сможет решить не такой уж маленький процент студентов!

Наверное, многие, ознакомившись с методическим материалом Подбор частного решения неоднородного уравнения, заметили, что в правой части рассматривается ограниченный класс функций 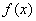: многочлены, экспоненты, синусы, косинусы.

Как быть, если в правой части 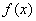находятся другие функции, например, тангенс или какая-нибудь дробь? И в таких случаях существует метод решения! Подбор не прокатывает, и приходится использовать очень мощный и универсальный метод вариации произвольных постоянных.

Решения и ответы: