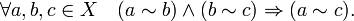Операции над множествами
Основными операциями над множествами являются объединение, пересечение и разность.
Определение 1. Объединением двух множеств называется новое множество

Определение 2. Пересечением двух множеств называется новое множество

Определение 3. Разностью двух множеств называется новое множество
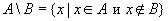
Если класс объектов, на которых определяются различные множества обозначить 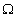 (Универсум), тодополнением множества
(Универсум), тодополнением множества 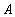 называют разность
называют разность
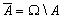
Отношение
Определение 6. Подмножество 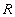 декартового произведения множеств
декартового произведения множеств 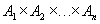 называетсяотношением степени n (n-арным отношением).
называетсяотношением степени n (n-арным отношением).
Определение 7. Мощность множества кортежей, входящих в отношение 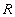 , называют мощностью отношения
, называют мощностью отношения 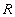 .
.
Замечание. Понятие отношения является очень важным не только с математической точки зрения. Понятие отношения фактически лежит в основе всей реляционной теории баз данных. Как будет показано ниже, отношения являются математическим аналогом таблиц. Сам термин "реляционное представление данных", впервые введенный Коддом [43], происходит от термина relation, понимаемом именно в смысле этого определения.
Т.к. любое множество можно рассматривать как декартовое произведение степени 1, то любое подмножество, как и любое множество, можно считать отношением степени 1. Это не очень интересный пример, свидетельствующий лишь о том, что термины "отношение степени 1" и "подмножество" являются синонимами. Нетривиальность понятия отношения проявляется, когда степень отношения больше 1. Ключевыми здесь являются два момента:
Во-первых, все элементы отношения есть однотипные кортежи. Однотипность кортежей позволяет считать их аналогами строк в простой таблице, т.е. в такой таблице, в которой все строки состоят из одинакового числа ячеек и в соответствующих ячейках содержатся одинаковые типы данных. Например, отношение, состоящее из трех следующих кортежей {(1, "Иванов", 1000), (2, "Петров", 2000), (3, "Сидоров", 3000)} можно считать таблицей, содержащей данные о сотрудниках и их зарплатах. Такая таблица будет иметь три строки и три колонки, причем в каждой колонке содержатся данные одного типа.
В противоположность этому рассмотрим множество {(1), (1, 2), (1, 2, 3)}, состоящее из разнотипныхчисловых кортежей. Это множество не является отношением ни в 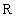 , ни в
, ни в 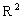 , ни в
, ни в 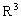 . Из кортежей, входящих в это множество нельзя составить простую таблицу. Правда, можно считать это множество отношением степени 1 на множестве всех возможных числовых кортежей всех возможных степеней
. Из кортежей, входящих в это множество нельзя составить простую таблицу. Правда, можно считать это множество отношением степени 1 на множестве всех возможных числовых кортежей всех возможных степеней 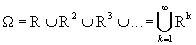 , но такая трактовка ничего нового, по сравнению с понятием подмножества, не дает.
, но такая трактовка ничего нового, по сравнению с понятием подмножества, не дает.
Во-вторых. За исключением крайнего случая, когда отношение есть само декартово произведение 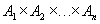 , отношение включает в себя не все возможные кортежи из декартового произведения. Это значит, что для каждого отношения имеется критерий, позволяющий определить, какие кортежи входят в отношение, а какие - нет. Этот критерий, по существу, определяет для нас смысл (семантику)отношения.
, отношение включает в себя не все возможные кортежи из декартового произведения. Это значит, что для каждого отношения имеется критерий, позволяющий определить, какие кортежи входят в отношение, а какие - нет. Этот критерий, по существу, определяет для нас смысл (семантику)отношения.
Действительно, каждому отношению можно поставить в соответствие некоторое логическое выражение 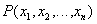 , зависящее от n параметров (n-местный предикат) и определяющее, будет ли кортеж
, зависящее от n параметров (n-местный предикат) и определяющее, будет ли кортеж 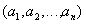 принадлежать отношению
принадлежать отношению 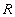 . Это логическое выражение называют предикатом отношения
. Это логическое выражение называют предикатом отношения 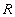 . Более точно, кортеж
. Более точно, кортеж 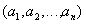 принадлежит отношению
принадлежит отношению 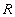 тогда и только тогда, когда предикат этого отношения
тогда и только тогда, когда предикат этого отношения 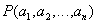 принимает значение "истина". В свою очередь, каждый n-местный предикат задает некоторое n-арное отношение. Таким образом, существует взаимно однозначное соответствие между n-арными отношениями и n-местными предикатами.
принимает значение "истина". В свою очередь, каждый n-местный предикат задает некоторое n-арное отношение. Таким образом, существует взаимно однозначное соответствие между n-арными отношениями и n-местными предикатами.
Если это не вызывает путаницы, удобно и отношение, и его предикат обозначать одной и той же буквой. Например, отношение 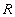 имеет предикат
имеет предикат 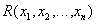 .
.
1.3
Отношение эквивалентности - это обобщение понятия равенства. Эквивалентные элементы не различимы для теории в каком-то фиксированном смысле.
Определение
Пусть дано множество 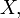 и на нём задано бинарное отношение
и на нём задано бинарное отношение 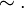 . Тогда
. Тогда 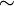 называется отношением эквивалентности, если оно
называется отношением эквивалентности, если оно
рефлексивно, то есть
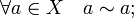
симметрично, то есть
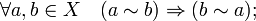
транзитивно, то есть