Как зависит выбор настроечного параметра а и уровня помех. Показать на качественном уровне на графике процесс сходимости коэффициентов при разном значении а и уровне помех

Параметр 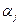выбирается из соображений оптимизации работы алгоритма. Определим его для предельного случая, когда структура модели и объекта совпадают, т. е.

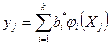. (5.80)

Подставив в формулы (5.78) и (5.79) соотношение (5.80) и выражение для вектора невязки параметров 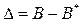, после некоторых преобразований получаем уравнение, отражающее изменение в процессе идентификации:

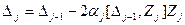
Тогда выражение для квадрата невязки имеет вид:

.

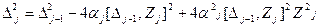Из условия минимизации этого выражения (дифференцированием по 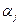и приравниванием нулю) и находится оптимальное [35] значение параметра :

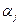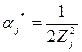. (5.81)

Тогда оптимальный алгоритм адаптивной шаговой идентификации принимает вид:

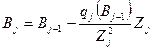
Алгоритмы автоматической подстройки моделей Челюсткина А Б. и Райбмана Н.С -----------

Известен ряд алгоритмов работы блоков автоматической подстройки (адаптации) моделей, среди которых можно отметить предложенный А. В. Челюсткиным метод, основанный на непрерывном расчете взаимной корреляционной функции

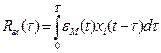(5.64)

Стремление к нулю величины 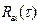свидетельствует об ослаблении влияния на ошибку модели 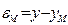данного входного параметра 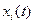. Следовательно, коэффициент 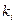при этом параметре целесообразно изменять в соответствии с правой частью уравнения (210)

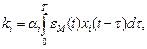
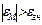(5.65)

где 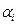– коэффициент, характеризующий интенсивность самонастройки;

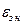– зона нечувствительности по ошибке модели, вводимая для снижения колебательности в контуре самонастройки.

Это соотношение сравнительно легко реализуется как программно, так и аппаратурно.

Можно отметить еще один алгоритм идентификации [34], который в непрерывной форме записывается выражением

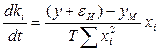(5.66)

где 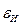– ошибка измерения выходной величины у;

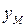– значение выходного параметра, получаемое на модели;

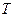– постоянная времени в контуре самонастройки.

Для сходимости алгоритма ошибка предсказания должна удовлетворять условию

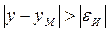(5.67)

Кроме дифференциальной формы записи выражение (5.66) отличается от (5.65) по существу лишь нормированием по сумме квадратов входных параметров, если учесть, что 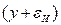– 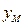есть ошибка модели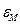

Основные этапы структурной идентификации----------

Среди задач вскрытия структуры объекта можно отметить следующие:

1) выделение объекта из среды;

2) ранжирование входов и выходов объекта по степени их влияния на конечный целевой показатель;

3) определение рационального числа входов и выходов объекта, учитываемых в модели;

4) определение характера связи между входом и выходом модели объекта, т. е. вида оператора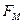

42----- Структурная схема управления объектом на основе прогнозирующей под­страиваемой модели-------

есть