Методические указания к решению задач контрольной работы.

Задания к контрольной работе

И методические указания к их выполнению

Математическая статистика (математика и статистика).

Задание 1.Из букв разрезной азбуки составлено некоторое слово. Карточки перемешаны и разложены в случайном порядке. Найти вероятность того, что получится первоначальное слово.

1.1 АСТРА 1.2 МОЛОКО 1.3 СЛАВА 1.4 ЗОЛОТО 1.5 СУММА 1.6 ТЕРЕМ

1.7ЛАГУНА 1.8 ССЫЛКА 1.9 ФИНИК 1.10 АЛМАЗ

Задание 2. В партии из n изделий m бракованных. Из партии для контроля выбирают k изделий. Найти вероятность того, что все выбранные изделия не бракованные.

2.1 n=30, m=5, k=4. 2.2n=25, m=3, k=5.

2.3 n=20, m=2, k=3. 2.4n=30, m=4, k=5.

2.5 n=20, m=4, k=5. 2.6 n=35, m=6, k=5.

2.7 n=25, m=4, k=2. 2.8 n=24, m=4, k=3.

2.9 n=30, m=6, k=3. 2.10 n=26, m=3, k=4.

Задание 3.Два стрелка стреляют одновременно в мишень. Первый стрелок попадает с вероятностью р₁, второй стрелок – с вероятностью р₂. Найти вероятности следующих событий: 1) оба стрелка попадут в мишень; 2) только один из стрелков попадет в мишень.

3.1 р₁ = 0.7, р₂ = 0.6. 3.2 р₁ = 0.8, р₂ = 0.5. 3.3 р₁ = 0.7, р₂ = 0.8. 3.4 р₁ = 0.6, р₂ = 0.8.

3.5 р₁ = 0.9, р₂ = 0.6. 3.6 р₁ = 0.7, р₂ = 0.9. 3.7 р₁ = 0.5, р₂ = 0.6. 3.8 р₁ = 0.8, р₂ = 0.9.

3.9 р₁ = 0.7, р₂ = 0.5. 3.10 р₁ = 0.8, р₂ = 0.4.

Задание 4. В первой урне n₁ белых и n₂ черных шаров, а во второй урне m₁ белых и m₂ черных шаров. Из каждой урны удалили по одному шару, а оставшиеся шары ссыпали в третью урну. Найти вероятность того, что случайно выбранный из третьей урны шар окажется белым.

4.1 n₁=2, n₂=8, m₁=5, m₂=3. 4.2 n₁=4, n₂=6, m₁=3, m₂=7.

4.3 n₁=5, n₂=5, m₁=4, m₂=6. 4.4 n₁=7, n₂=3, m₁=6, m₂=2.

4.5 n₁=6, n₂=4, m₁=5, m₂=4. 4.6 n₁=3, n₂=7, m₁=4, m₂=4.

4.7 n₁=8, n₂=2, m₁=2, m₂=6. 4.8 n₁=1, n₂=9, m₁=5, m₂=5.

4.9n₁=2, n₂=8, m₁=2, m₂=4. 4.10 n₁=5, n₂=6, m₁=2, m₂=8.

Задание 5.Купленоn билетов лотереи, вероятность выигрыша одного билета равна p. Найти наивероятнейшее число выигравших билетов и вероятность этого числа.

5.1n= 12, p = 0.2 5.2n= 10, p = 0.3 5.3n= 10, p = 0.1 5.4n= 8, p = 0.2

5.5n= 15, p = 0.3 5.6n= 12, p = 0.1 5.7n= 10, p = 0.2 5.8n= 15, p = 0.1

5.9n= 14, p = 0.2 5.10n= 12, p = 0.3

Задание 6. По выборке объема n=50 составлен вариационный ряд. Найти: а) частоту n₃; б) среднюю выборочную 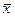; в) исправленную дисперсию 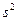; г) стандартное отклонение 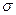; д) начертить полигон частот.

xi
ni			n3

6.1

xi	-1
ni			n3

6.2

xi	-6	-3	-2
ni			n3

6.3

xi
ni			n3

6.4

xi	-4	-2	-1
ni			n3

6.5

xi	-2
ni			n3

6.6

xi	-10	-5	-3
ni			n3

6.7

xi
ni			n3

6.8

xi	-1
ni			n3

6.9

xi	-7	-3	-1
ni			n3

6.10

Методические указания к решению задач контрольной работы.

Задание 1.Из букв разрезной азбуки составлено слово ХОРОШО. Карточки перемешаны и разложены в случайном порядке. Найти вероятность того, что получится первоначальное слово.

Решение. Обозначим: событие А – «получится первоначальное слово ХОРОШО». Вероятность этого события вычислим по формуле классической вероятности: 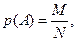где N – количество всех возможных исходов опыта, а M – количество исходов опыта, благоприятствующих событию А.

В слове 6 букв, поэтому количество всех возможных «слов» равно: N = P₆ = 6! = 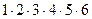=720

В слове 3 буквы О, от их перестановки слово не изменится, поэтому количество исходов опыта, благоприятствующих событию А: М = Р₃ = 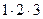= 6.

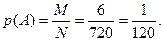
Задание 2. В партии из 30 изделий 2 бракованных. Из партии для контроля выбирают 6 изделий. Найти вероятность того, что все выбранные изделия не бракованные.

Решение.Обозначим событие А – «все выбранные изделия не бракованные». Вероятность этого события вычислим по формуле классической вероятности: 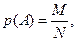где N – количество всех возможных исходов опыта, а M – количество исходов опыта, благоприятствующих событию А.

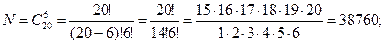
Количество не бракованных изделий равно: 20 – 2 = 18. Тогда:

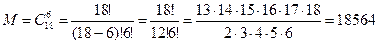
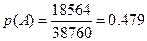
Задание 3.Два стрелка стреляют одновременно в мишень. Первый стрелок попадает с вероятностью 0.9, второй стрелок – с вероятностью 0.5. Найти вероятности следующих событий: 1) оба стрелка попадут в мишень; 2) только один из стрелков попадет в мишень.

Решение.Обозначим события:

А – «первый стрелок попал», по условию р(А)=0.9

В – «второй стрелок попал», по условию р(В)=0.5

С – «оба стрелка попадут», С =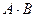

D – «только один из стрелков попадет», D = 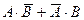. Тогда:

р(А) = р(А) р(В) = 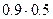= 0.45;

р(D) = 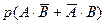= = 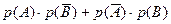= 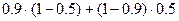0.50

Задание 4. В первой урне 5 белых и 3 черных шара, а во второй урне 6 белых и 4 черных шара. Из каждой урны удалили по одному шару, а оставшиеся шары ссыпали в третью урну. Найти вероятность того, что случайно выбранный из третьей урны шар окажется белым.

Решение.В этой задаче опыт производится в два этапа: сначала шары удаляются из урн и ссыпаются в третью урну, а потом из третьей урны берется один шар. Такие задачи решают с помощью формулы полной вероятности:

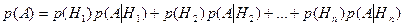
В 1-ой урне 5 + 3 = 8 шаров; во 2-й: 6 + 4 = 10 шаров.

1) Сформулируем гипотезы:

Н₁: из 1-ой урны удалили белый шар, из 2-ой – белый;

Н₂: из 1-ой урны удалили белый шар, из 2-ой – черный;

Н₃: из 1-ой урны удалили черный шар, из 2-ой – белый;

Н₄: из 1-ой урны удалили черный шар, из 1-ой – черный;

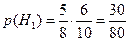
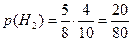
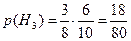
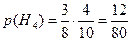
Проверка: .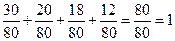

2) Событие А – из 3-й урны взят белый шар. В 1-ой урне осталось 8 – 1 = 7 шаров, во 2-ой: 10 – 1 =9 шаров. В 3-ю урну ссыпали 7+9 = 16 шаров. Найдем условные вероятности:

; .

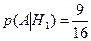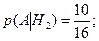
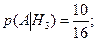
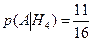По формуле полной вероятности:

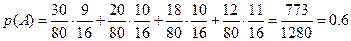
Задание 5.Куплено15 билетов лотереи, вероятность выигрыша одного билета равна 0.2. Найти наивероятнейшее число выигравших билетов и вероятность этого числа.

Решение.Рассмотрим схему Бернулли, n= 15, p = 0.2, q = 1 - p = 1 - 0.2 = 0.8;

наивероятнейшее число m выигравших билетов находится по формуле:

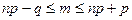
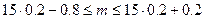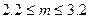; ; m = 3.

Вероятность этого числа находим по формуле Бернулли:

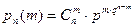
Подставим в формулу данные, получим:

=

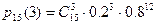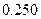
Задание 6.По выборке объема n=50 составлен вариационный ряд. Найти: а) частоту n₃; б) среднюю выборочную 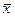; в) исправленную дисперсию 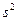; г) стандартное отклонение 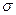; д) начертить полигон частот.

xi
ni			n3

Решение. а). Сумма всех частот равна объему выборки: 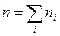, тогда 50 = 11 + 9+ n₃+ 12+10, поэтому

n₃= 50 - (11+9+12+10) = 8;

б) 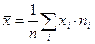= =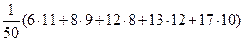1.2

в) исправленная дисперсия: ;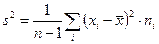

S² 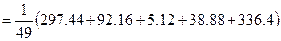=15.71

г) стандартное отклонение 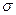находится по формуле: = =

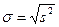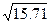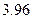
д) начертить полигон частот.

Литература