Тема №6. Теория вероятностей и математическая статистика

Случайные события

Случайное событие

Случайным называется событие, которое при проведении опыта либо происходит, либо нет.

Такими простейшими опытами являются подбрасывание монеты или бросание игральной кости. С подбрасыванием монеты связаны два случайных события: падение герба или решки; с бросанием игральной кости связаны 6 случайных события: выпадение чисел 1, 2, 3, 4, 5, 6.

þ Обозначение: События обозначают первыми прописными буквами латинского алфавита А, В, С …

1. События А и В несовместны, если в результате одного опыта они не могут происходить одновременно, в противном случае они совместны.

! Пример: Падение герба и решки одновременно не возможно, поэтому эти события несовместны. Появление четного числа и 2 одновременно возможно, поэтому эти события совместны.

2. События равновозможные, если ни одно из них не имеет объективного преимущества перед другими.

! Пример: Падение герба и решки равновозможные события.

3. События A₁, A₂, … A_n образуют полную группу, если в результате опыта кроме этих событий ничего не может произойти.

! Пример: Выпадение чисел 1, 2, 3, 4, 5, 6 события, образующие полную группу.

4. Два события A и B называются независимыми, если появление одного из них не влияет на вероятность появления другого (в противном случае события зависимы).

! Пример: Выпадение числа 2 в первом бросания не влияет на выпадение числа 3 во втором бросания.

5. События A и 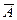называются противоположными или взаимно дополняющими, если не появление одной из них в результате данного опыта влечет появление другого.

Следует отметить, что события A и 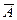несовместны.

! Пример: События «изделие бракованное» и «изделие» стандартное – противоположные. Изделие не может одновременно быть и стандартным и бракованным.

Операция над событиями

Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из них в результате опыта.

Сумма двух событий зависит от того, с какими событиями мы имеем дело.

Если события A и B совместные, то сумма A + B означает, что наступит событие A, или событие B, или оба события вместе.

! Пример: Появление 4 очков (событие A) означает появление события четного числа (событие B).

Если события A и B несовместные, то сумма A + B означает, что наступит событие A, или событие B, так как наступление событий A и B одновременно невозможно. В этом случае знак суммы заменяет союз или.

! Пример: Событие появления меньше 3 очков это то же самое, что появление или 1 очка или 2 очков.

Произведением двух событий называется событие, состоящее в совместном наступлении этих событий в результате опыта.

Знак произведения заменяет союз и.

! Пример: Если событие A это событие, что из колоды карт вынута «дама», а событие B - вынута карта пиковой масти, тогда AB есть событие, что вынута «дама пик».

Частота и вероятность. Основные формулы для вычисления вероятностей

Вероятность

Вероятностью события А называется отношение числа исходов m поступления события А к числу всевозможных исходов n:

.

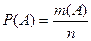Это есть классическое определение вероятности случайного события.

þ Обозначение: Вероятность обозначается буквой p (от английского слова «probability»).

! Примеры: Вероятность выпадения решки, при подбрасывания монеты, равна ½; вероятность появления числа 2 при бросания игральной кости равна 1/6.

@ Задача 1: Пусть брошена игральная кость. Найти вероятность выпадения числа больше 4.

Решение: Из возможных 6 исходов только при 2 исходах выпавшее число будет больше 4 (это выпадение чисел 5 и 6). Следовательно, P = 2/6 = 1/3.

@ Задача 2: Брошены две игральные кости. Найти вероятность того, что: а) сумма выпавших очков четная; б) произведение выпавших очков больше 20.

Решение: Число всех возможных исходов равно 36. Событие А (сумма выпавших очков четная) насчитывает 18 исходов (случаев), а событие В (произведение выпавших очков больше 20) – 6 исходов (случаев) ((4; 6), (5; 5), (5; 6), (6; 4), (6; 5), (6; 6)). Следовательно, P(А) = 18/36 = ½; P(В) = 6/36 = 1/6.

Свойства вероятности

1. Вероятность положительная и не может быть больше единицы. 0 £ P(A) £ 1

2. Если события А и В несовместны, то вероятность объединенного события равна сумме вероятностей: P(A + B) = P(A) + P(B).

3. Если события A₁, A₂, … A_n образуют полную группу, то P(A₁ + A₂ + … + A_n) = 1. Сумма вероятностей противоположных событий равна 1, потому что они составляют полную группу.

4. Если события А и В совместны, то P(A + B) = P(A) + P(B) – P(A·B), где P(A·B) – вероятность произведения событий A и B.

5. Если события А и В независимые, то P(A·B) = P(A)·P(B).

Условная вероятность

Условной вероятностью события В при условии, что событие А уже произошло, называется вероятность .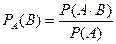

Из условной вероятности легко получить формулу умножения вероятностей для двух событий: P(A×B) = P(A)×P_A(B). Вероятность произведения трех событий равна P(A×B×C) = P(A)×P_A(B)×P_A×B(C).

@ Задача 3: В урне лежат три белых, три черных и три желтых шара. Наугад берем три шара. Найти вероятность того, что все три шара окажутся: а) белого цвета; б) одинакового цвета; в) разного цвета.

Решение: а) Вероятность того, что первый шар белый равен 1/3, второй белый - 2/8, третий белый - 1/7. По формуле произведения вероятностей получим P = 1/3·2/8·1/7 = 1/84. б) Допустим, что первый вынутый шар белый (черный или желтый), тогда вероятность того, что второй шар тоже белый (черный или желтый), равна 2/8. Вероятность того, что третий шар тоже белый (черный или желтый), равна 1/7. По формуле произведения вероятностей получим P = 1·2/8·1/7 = 1/28. в) Допустим, что первый вынутый шар белый (черный или желтый), тогда вероятность того, что второй шар не белый, равна 6/8. Вероятность того, что третий шар желтый (черный), равна 3/7. По формуле произведения вероятностей получим P = 1·6/8·3/7 = 9/28.

Случайные величины.

Случайная величина