Создание схемы реального колебательного контура
Добавим в схему активное сопротивление R = 1 Ом, удовлетворяющее соотношению (20) – см. рис. 12.
Анализ затухания колебаний в контуре с помощью функции Transient Analysis
Проведем моделирование процессов в контуре с активным сопротивлением, изменив в настройках функции Transient Analysis (см. п. 4. 2) только время моделирования (см. рис. 6). Для большей наглядности графика увеличим временной интервал анализа, поставив TSTOP = 5 с.
После редактирования, аналогичного проведенному в п. 4. 2, получим график, изображенный на рис. 13.
Курсоры на графике отмечают положения двух «первых» максимумов напряжения на контуре:
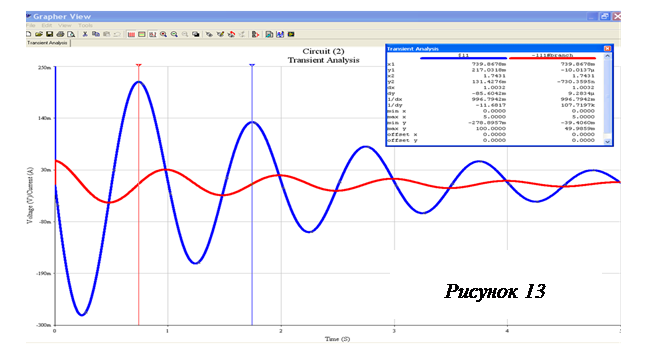I m1 = 217,0318 мВ; I m2 = 131,4276 мВ.
Следующие максимумы:
U m3 = 79,5884 мВ; U m4 = 48,1962 мВ; U m5 = 29,1861 мВ.
Отношение любых двух из последовательных максимумов
.
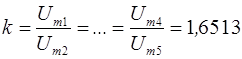Натуральный логарифм коэффициента k
;
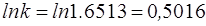с учетом небольшой погрешности вычислений равен декременту затухания, рассчитанному по формуле (18):
.
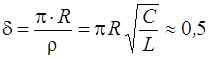В е раз колебания контура затухают за два условных периода.
Задание 2: Увеличив активное сопротивление контура в два раза, рассчитайте и определите графически декремент затухания.
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ НА ЛАБОРАТОРНОЕ ИССЛЕДОВАНИЕ
Собрав соответствующие схемы (см. рис. 3 и 12), выполните анализ колебаний идеального контура и контура с активным сопротивлением.
Рассчитайте следующие величины, характеризующие свободные колебания:
- круговая и линейная частоты;
- период;
- длина волны;
- волновое сопротивление контура;
- декремент затухания;
- добротность контура.
Воспользовавшись графиками кривых тока в контуре и напряжения на контуре (полученным с помощью функции Transient Analysis – см., для примера, рис. 10 и рис. 13), проверьте соответствие теоретических результатов экспериментальным.
Параметры используемых компонентов указаны в табл. 1.
Вариант задания для каждого студента соответствует его номеру в списке подгруппы/группы в журнале преподавателя.
Таблица 1
| № варианта | ||||||
| Ёмкость С, мкФ | ||||||
| Индуктивность L, мГн | 6,3350 | 2,5350 | 4,0530 | 0,5404 | 1,2665 | 3,8970 |
| Сопротивление R, Ом | 1,2670 | 1,0140 | 5,0662 | 6,7550 | 1,0135 | 1,9485 |
| № варианта | ||||||
| Ёмкость С, мкФ | ||||||
| Индуктивность L, мГн | 4,2217 | 0,5066 | 6,7053 | 0,8142 | 5,0660 | 2,8500 |
| Сопротивление R, Ом | 3,3760 | 2,5330 | 1,1176 | 3,2570 | 10,134 | 7,5996 |
Замечание: при отсутствии возможности установить значение параметра с требуемой точностью используйте меньшие единицами измерения, переведя, например, миллигенри в микрогенри.
Параметры импульсного источника подберите для обеих схем самостоятельно.
Время моделирования для схемы реального колебательного контура установите, учитывая количества периодов, необходимое для значительного уменьшения амплитуды колебаний.
СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы.
2. Основные формулы, используемые при расчетах требуемых характеристик колебательных контуров.
3. Подробная запись всех этапов проведенных расчетов и их результаты.
4. Скриншоты графиков, полученных в результате проведения Transient Analysis, с открытыми окнами курсоров.
5. Сопоставление расчетных данных с результатами моделирования.
6. Выводы.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1.Попов, В. П. Основы теории цепей / В. П. Попов. – 3-е изд., испр. – М.: Высш. шк., 2000 – 575 с.
2.Исследование резистивных схемных соединений в цепях постоянного тока: методические указания по выполнению лабораторной работы по дисциплине «Теория электрических цепей» / Юго-Зап. гос. ун-т; сост.: Л. А. Болычевцева, А. Ф. Рыбочкин. Курск, 2013. 22 с.
3.Исследование линейных цепей при гармоническом воздействии : методические указания по выполнению лабораторной работы по дисциплине «Теория электрических цепей» / Юго-Зап. гос. ун-т; сост.: Л. А. Болычевцева, А. Ф. Рыбочкин. Курск, 2013. 31 с.: ил. 24, табл. 1. Библиогр.: с. 31.
