Контрольная работа № 2. 1.Найти предел:
1.Найти предел:
.
2.При каких значениях параметра касательная к гиперболе пересекает ось абсцисс в точке . Сделать чертеж.
| 3.Исследовать функцию и построить схематично ее график. |
| . 4. Вычислить определенный интеграл: |
5Вычислить площадь фигуры, ограниченной линиями , , , . Сделать чертеж.
6.Экспериментальные данные о переменных х и у приведены в таблице:
| 2,5 | 4,0 | 5,1 | 6,5 | 7,4 |
В результате их выравнивания получена функция . Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
7.Решить дифференциальное уравнение:
.
8. Исследовать сходимость ряда:
.
ВАРИАНТ 6
(для студентов, номера личных дел которых оканчиваются цифрой 6)
Контрольная работа № 1
1.Даны матрицы
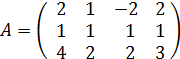 и
и 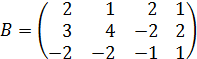 .
.
Установить, имеет ли матрица 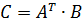 обратную.
обратную.
2.Методом обратной матрицы решить систему:
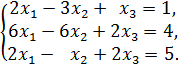
3.Решить систему линейных уравнений:
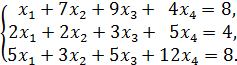
Найти какое-нибудь базисное решение.
4. Даны четыре вектора
=(– 2;1;7); =(3; – 3;8); =(5;4;1); =(18;25;1)
в некотором базисе. Показать, что векторы , , образуют базис, и найти координаты вектора в этом базисе.
5. а) Методом Лагранжа привести квадратичную форму
f(x1, x2)=4x12+ x22–4x1x2
к каноническому виду (указать пример соответствующего преобразования координат).
б)По критерию Сильвестра исследовать на знакоопределенность квадратичную форму
f(x1, x2, x3)= 2x12+x22+3x32 +2x1x2–2x1x3 –2x2x3..
6. Вычислить радиус окружности, вписанной в треугольник, у которого две биссектрисы лежат на прямых и , а одна из его сторон на прямой . Сделать чертеж.
7. Найти угол между плоскостями и .
Контрольная работа № 2
1.Найти предел:
.
2.Написать уравнение касательных к гиперболе , перпендикулярных прямой . Сделать чертеж.
| 3. Исследовать функцию и построить схематично ее график. |
| 4. Вычислить определенный интеграл: |
5. Вычислить площадь фигуры, ограниченной линиями , , . Сделать чертеж.
6. Экспериментальные данные о переменных х и у приведены в таблице:
В результате их выравнивания получена функция . Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
7.Решить дифференциальное уравнение:
.
8. Исследовать сходимость ряда:
.
ВАРИАНТ 7
(для студентов, номера личных дел которых оканчиваются цифрой 7)
