Сила всемирного тяготения

Все тела взаимодействуют друг с другом. Это предположение зародилось у Ньютона в 1667 году. Ньютон понимал, что для того, чтобы Луна вращалась вокруг Земли, а Земля и другие планеты вокруг Солнца, должна существовать сила, удерживающая их на круговой орбите. Он предположил, что сила тяжести, действующая на все тела на Земле и сила, удерживающая планеты на их круговых орбитах, есть одна и та же сила. Эта сила получила название сила всемирного тяготения или гравитационная сила. Эта сила является силой притяжения и действует между всеми телами. Ньютон сформулировал закон всемирного тяготения: две материальные точки притягиваются друг к другу с силой прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.

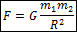
Коэффициент пропорциональности G во времена Ньютона был неизвестен. Впервые он был экспериментально измерен английским ученым Кавендишем. Этот коэффициент называется гравитационной постоянной. Ее современное значение равно 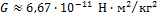. Гравитационная постоянная является одной из самых фундаментальных физических констант. Закон всемирного тяготения можно записать в векторном виде. Если сила, действующая на вторую точку со стороны первой равна F₂₁, а радиус-вектор второй точки относительно первой равен R₂₁, то:

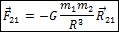
Представленный вид закона всемирного тяготения справедлив только для гравитационного взаимодействия материальных точек. Для тел произвольной формы и размеров его использовать нельзя. Вычисление гравитационной силы в общем случае является очень непростой задачей. Однако, есть тела, не являющиеся материальными точками, для которых гравитационную силу можно считать по приведенной формуле. Это тела, обладающие сферической симметрией, например, имеющие форму шара. Для таких тел приведенный закон справедлив, если под расстоянием R понимать расстояние между центрами тел. В частности силу тяжести, действующую на все тела со стороны Земли можно считать по этой формуле, так как Земля имеет форму шара, а все остальные тела можно считать материальными точками по сравнению с радиусом Земли.

Так как сила тяжести является гравитационной силой, то можно написать, что сила тяжести, действующая на тело массой m равна

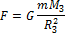
Где М_З и R_З – масса и радиус Земли. С другой стороны сила тяжести равна mg, где g – ускорение свободного падения. Значит ускорение свободного падения равно

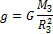
Это формула для ускорения свободного падения на поверхности Земли. Если удаляться от поверхности Земли, то расстояние до центра Земли будет увеличиваться, а ускорение свободного падения соответственно уменьшаться. Так на высоте h над поверхностью Земли ускорение свободного падения равно:

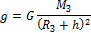
Гидростатика

Идеальной жидкостью называется несжимаемая и невязкая жидкость.

на тело, погруженное в жидкость, действует выталкивающая сила, равная силе тяжести жидкости в объеме погруженной части тела.

Здесь ρ_ж – плотность жидкости; V_пог – объем погруженной части тела.

Сила Архимеда, как и любая другая сила, имеет точку своего приложения. Точкой приложения силы Архимеда является центр тяжести жидкости в погруженном объеме тела.

Если тело опустить в жидкость, то оно либо плавает на ее поверхности, либо тонет. Это зависит от соотношения плотностей тела и жидкости. Если плотность тела меньше, чем плотность жидкости, то тело плавает на ее поверхности. При этом тело частично погружено в жидкость и его сила тяжести уравновешивается силой Архимеда:

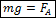
Это уравнение называется условием плавания тела. Если плотность тела больше плотности жидкости, то тело тонет. При этом оно либо давит на дно сосуда, либо натягивает нить подвеса. Эта сила называется весом тела. Вес тела погруженного в жидкость равен разнице силы тяжести и силы Архимеда:

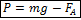
Заметим, что если тело плавает на поверхности жидкости, то его вес равен нулю.

Устойчивость плавания.

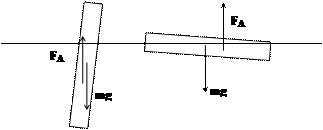Рассмотрим устойчивость плавания тел на поверхности жидкости. Пусть на поверхности жидкости плавает однородный стержень, плотность которого меньше плотности жидкости. Имеется два положения равновесия плавания стержня: вертикальное и горизонтальное. Сила тяжести приложена в центре тяжести стержня, а сила Архимеда в центре тяжести погруженной части стержня. Если стержень находится в строго вертикальном, или в строго горизонтальном положении, то эти две силы направлены вдоль одной прямой и компенсируют друг друга. Однако, при случайных колебаниях поверхности воды, эти положения равновесия могут нарушиться и стержень отклонится в сторону. При этом возникнет момент силы тяжести и силы Архимеда. Из рисунка вино, что при отклонении стержня от вертикального положения этот момент сил будет опрокидывать стержень, а при отклонении от горизонтального положения будет возвращать его в исходное положение. Значит, вертикальное положение плавания стержня будет неустойчивым, а горизонтальное – устойчивым.

Вопросы устойчивости плавания очень важны при проектировании судов. Рассмотрим корабль, отклонившийся от вертикального положения. Пусть ось ОО₁ – ось симметрии корабля. Точка приложения силы тяжести находится на оси ОО₁, а силы Архимеда в центре тяжести погруженного объема корабля. Точка пересечения линии действия выталкивающей силы с осью ОО₁ (точка N) называется метацентром. Если метацентр находится выше точки приложения силы тяжести, то положение корабля устойчивое, а если ниже, то неустойчивое.