Напряжение в точке. Полное, нормальное, касательное напряжения. Размерности напряжения
Напряжение – мера распределения внутренних сил по сечению.
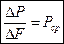 , где
, где 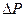 - внутренняя сила, выявленная на площадке
- внутренняя сила, выявленная на площадке 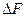 .
.
Полное напряжение 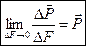 .
.
Нормальное напряжение – проекция вектора полного напряжения на нормаль обозначается через σ. 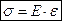 , где Е – модуль упругости I рода, ε – линейная деформация. Нормальное напряжения вызывается только изменением длин волокон, направлением их действий, а угол поперечных и продольных волокон не искажается.
, где Е – модуль упругости I рода, ε – линейная деформация. Нормальное напряжения вызывается только изменением длин волокон, направлением их действий, а угол поперечных и продольных волокон не искажается.
Касательное напряжение – составляющие напряжения в плоскости сечения. 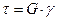 , где
, где 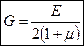 (для изотропного материала) – модуль сдвига (модуль упругости II рода), μ – коэффициент Пуассона (=0,3), γ – угол сдвига.
(для изотропного материала) – модуль сдвига (модуль упругости II рода), μ – коэффициент Пуассона (=0,3), γ – угол сдвига.
Закон Гука для одноосного напряжённого состояния в точке и закон Гука для чистого сдвига. Модули упругости первого и второго рода, их физический смысл, математический смысл и графическая интерпретация. Коэффициент Пуассона.
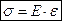 - закон Гука для одноосного напряжённого состояния в точке.
- закон Гука для одноосного напряжённого состояния в точке.
Е – коэффициент пропорциональности (модуль упругости I рода). Модуль упругости является физической константой материала и определяется экспериментально. Величина Е измеряется в тех же единицах, что и σ, т.е. в кГ/см2.
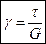 - закон Гука для сдвига.
- закон Гука для сдвига.
G – модуль сдвига (модуль упругости II рода). Размерность модуля G такая же, как и у модуля Е, т.е. кГ/см2. 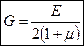 .
.
μ – коэффициент Пуассона (коэффициент пропорциональности). 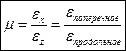 . Безразмерная величина, характеризующая свойства материала и определяющаяся экспериментально и лежит в интервале от 0,25 до 0,35 и не могут превышают 0,5 (для изотропного материала).
. Безразмерная величина, характеризующая свойства материала и определяющаяся экспериментально и лежит в интервале от 0,25 до 0,35 и не могут превышают 0,5 (для изотропного материала).
Центральное растяжение (сжатие) прямого бруса. Определение внутренних продольных сил методом сечений. Правило знаков для внутренних продольных сил. Привести примеры расчёта внутренних продольных сил.
Брус испытывает состояние центрального растяжения (сжатия) в том случае, если в его поперечных сечениях возникают центральные продольные силы Nz (т.е. внутренняя сила, линия действия которой направлена по оси z), а остальные 5 силовых факторов равны нулю (Qx=Qy=Mx=My=Mz=0).
Правило знаков для Nz: истинная растягивающая сила – «+», истинная сжимающая сила – «-».
Центральное растяжение (сжатие) прямого бруса. Постановка и решение задачи об определении напряжений в поперечных сечениях бруса. Три стороны задачи.
Центральное напряжение (сж.) прямого бруса см. в вопросе 8.
Постановка: Прямой брус из однородного материала, растянутый (сжатый) центральными продольными силами N. Определить напряжение, возникающее в поперечных сечениях бруса, деформации и перемещения поперечных сечений бруса в зависимости от координат z этих сечений.