Утверждение о числе функций от n переменных
Теорема: Число различных (неодинаковых) булевых функций от n переменных есть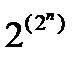
.
Теорема будет следовать из следующего утверждения:
число различных двоичных наборов длины n есть 2n (под длиной набора подразумевается число цифр в нем).
Докажем утверждение индукцией по длине n набора.
Для n=1 имеем 0;1 два различных набора длины 1;
21 =2. Для n=1 утверждение индукции справедливо.
Пусть утверждение индукции справедливо для n³1, то есть число различных двоичных наборов длины n³1 есть - 2n.
Покажем справедливость утверждения для n=n+1. Разобьем все двоичные наборы длины n+1 на две группы. В первую группу отнесем двоичные наборы, которые начинаются на 0. Во вторую группу отнесем двоичные наборы, которые начинаются на 1, например, для n+1 = 3 будет такое разбиение:
Двоичные наборы первой (второй) группы получаются из всевозможных двоичных наборов длины n добавлением слева нуля (единицы) к всевозможным наборам длины n.
Но по предположению индукции наборов длины n имеется 2n, поэтому число наборов как в первой, так и во второй группе будет 2n, поэтому общее число наборов длины (n+1) будет 2n+2n = 2n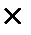 
2 = 2n+1
Утверждение доказано.
| x1 | … | xn | f(x1…xn) | |
| 0 | … | * | ||
| … | … | … | |
| … | * |
Функций от n переменных будет ровно столько, сколько существует разных двоичных наборов длины 2n.
По предыдущему утверждению это число есть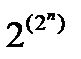 
. Теорема доказана.
Определение :
Элементарной конъюнкцией на множестве переменных {x1…xn} называют функцию логического произведения множителей , где каждый множитель либо переменная, либо отрицание переменной.
В дальнейшем значение 
в элементарной конъюнкции будем опускать или заменять 
.
Например: { x1 x2 x3 x4 }
x1 x2 x4 ; эта функция равна 1, только на одном наборе:
1 0 1 x1 x2 x4=1
x1 x2 x4
Рангом конъюнкции называют число переменных конъюнкции. Далее будем считать, что все переменные в множителях элементарных конъюнкций различны. В противном случае, используя правила :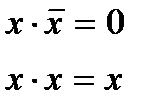 
, приведем конъюнкции к нужном виду;
Например: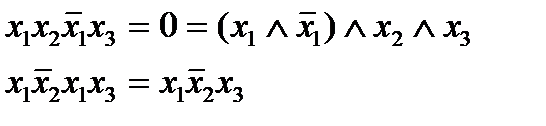 
полученная конъюнкция будет тождественно равна первоначальной.
В силу коммутативности и ассоциативности бинарной конъюнкции, две приведенные конъюнкции равны, т . и т. т., когда они состоят из одного набора множителей.
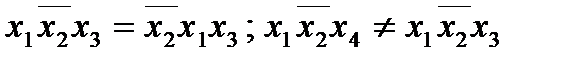
Определение
Элементарной дизъюнкцией на множестве переменных {x1…xn} называют функцию логического сложения слагаемых , где каждое слагаемое либо переменная, либо отрицание переменной.
Например: { x1 x2 x3 x4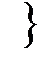 
x1 
x2 x4 ; эта функция равна 0, т. и т.т., когда все слагаемые равны 0. т.е. на наборах 0110 и 0100
Рангом дизъюнкции называют число слагаемых дизъюнкции. Далее будем считать, что все переменные в множителях элементарных дизъюнкций различны . В противном случае , используя правила :
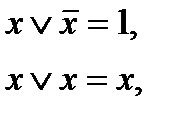
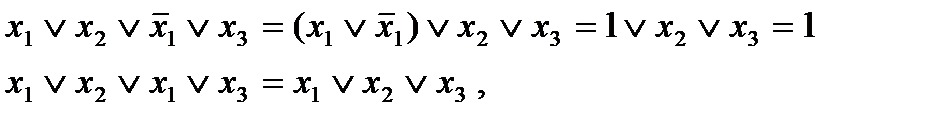
приведем дизъюнкции к нужном виду; полученная дизъюнкция будет тождественно равна первоначальной.
В силу коммутативности и ассоциативности элементарные дизъюнкции равны, т . и т. т., когда они состоят из одного и того же набора слагаемых.
Дизъюнктивной нормальной формой (ДНФ) на множестве переменных (x1…xn) называют функцию логического сложения некоторых слагаемых, где каждое слагаемое есть элементарная конъюнкция на (x1…xn) :
{ x1 x2 x3 x4 }
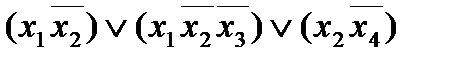
ДНФ называется совершенной (СДНФ), если каждая элементарная конъюнкция имеет ранг n :
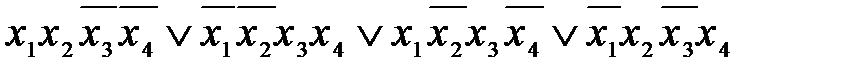
Далее считаем, что слагаемые ДНФ не повторяются (в противном случае можно
Множество единиц ДНФ есть объединение множества единиц элементарных конъюнкций ДНФ. Каждая элементарная конъюнкция полного ранга имеет единственную единицу. Слагаемые СДНФ (элементарные конъюнкции полного ранга) и единицы СДНФ находятся во взаимнооднозначном соответствии.