Маршруты, цепи и циклы
Маршрутом в графе называется чередующаяся последовательность вершин и ребер 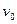
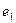
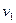
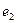
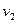 …
… 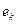
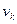 , в которой любые два соседних элемента инцидентны. Если
, в которой любые два соседних элемента инцидентны. Если 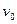 =
= 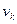 , то маршрут называется замкнутым, а если
, то маршрут называется замкнутым, а если 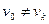 , то – открытым.
, то – открытым.
Длиной маршрута считается число ребер, которые он содержит.
Маршрут называется цепью, если каждое ребро встречается в нем не более одного раза. Цепь, в которой все вершины различны, называется простой цепью.
Замкнутая цепь называется циклом, а простая замкнутая цепь – простым циклом.
Если есть цепь, соединяющая две вершины 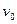 и
и 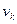 , то есть и простая цепь, соединяющая эти вершины. Две вершины называются связными, если существует связывающая их простая сеть; в противном случае вершины называются несвязными.
, то есть и простая цепь, соединяющая эти вершины. Две вершины называются связными, если существует связывающая их простая сеть; в противном случае вершины называются несвязными.
Граф называется связным, если каждые две его вершины связные; в противном случае – несвязным.
Деревья
Неориентированный граф называется деревом, если он связен и не имеет циклов.
Основные свойства деревьев:
– любые две вершины дерева можно соединить ровно одной простой цепью;
– если дерево G содержит хотя бы одно ребро, на нем найдется висячая вершина;
– число ребер дерева G на единицу меньше числа его вершин.
Справедливо и обратное утверждение: если у связного графа число ребер на единицу меньше числа вершин, то такой граф является деревом.
Дерево 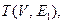 множество вершин которого совпадает с множеством вершин графа
множество вершин которого совпадает с множеством вершин графа 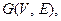 а ребра являются ребрами графа G(
а ребра являются ребрами графа G( 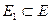 ), называется остовным (покрывающим) деревом графа G. Иными словами, остовное дерево графа G – это его подграф, содержащий все вершины и являющийся деревом.
), называется остовным (покрывающим) деревом графа G. Иными словами, остовное дерево графа G – это его подграф, содержащий все вершины и являющийся деревом.
Если n – число вершин, а m – число ребер графа G, то любое его остовное дерево имеет n вершин и (n – 1) ребер. Таким образом, остовное дерево получается отбрасыванием (m – n + 1) ребер графа G. Число 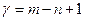 называется цикломатическим числом графа G.
называется цикломатическим числом графа G.
Если каждому ребру графа приписано некоторое положительное число, называемое его весом или стоимостью, то граф называется нагруженным. Стоимостью нагруженного графа считается суммарная стоимость всех его ребер. Многие задачи, связанные с построением экономичных систем сообщения или информационных систем, приводят к задаче поиска остовного дерева минимальной стоимости.
Пример 11.Построить остовное дерево минимальной стоимости для графа, представленного на рисунке 6. Определить его стоимость.
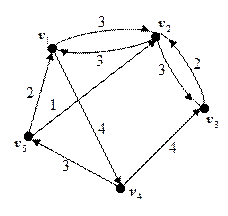
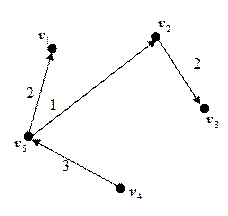
Рис. 6 Рис. 7
Р е ш е н и е. Остовное дерево содержит все вершины исходного графа, т.е. в нем будет 5 вершин и 4 ребра. Прежде всего, найдем на нагруженном графе самое легкое ребро. В данном случае это ребро, соединяющее вторую и пятую вершины 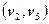 и имеющее стоимость 1. Это будет первым ребром остовного дерева минимальной стоимости (рис. 7).
и имеющее стоимость 1. Это будет первым ребром остовного дерева минимальной стоимости (рис. 7).
Теперь среди оставшихся ребер выберем следующие по стоимости ребра 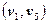 и
и 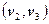 . Поскольку оба они соединяют одну из уже отобранных в оставное дерево вершину
. Поскольку оба они соединяют одну из уже отобранных в оставное дерево вершину 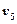 или
или 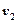 с новой, еще не присоединенной вершиной
с новой, еще не присоединенной вершиной 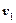 и
и 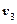 соответственно, то оба эти ребра нужно добавить к дереву.
соответственно, то оба эти ребра нужно добавить к дереву.
Среди ребер стоимостью 3 два ребра 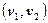 и
и 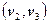 соединяют между собой вершины, уже присоединенные к дереву, и, следовательно, не могут быть включены в него. Третье ребро
соединяют между собой вершины, уже присоединенные к дереву, и, следовательно, не могут быть включены в него. Третье ребро 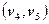 соединяет вершину дерева
соединяет вершину дерева 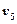 с еще не присоединенной вершиной
с еще не присоединенной вершиной 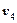 , т.е. может быть присоединено к дереву. Получившееся остовное дерево имеет минимальную стоимость, которая равна сумме стоимостей ребер в него отобранных: 1+2+2+3 = 8.►
, т.е. может быть присоединено к дереву. Получившееся остовное дерево имеет минимальную стоимость, которая равна сумме стоимостей ребер в него отобранных: 1+2+2+3 = 8.►
Тема 5. Теория алгоритмов
Общее понятие алгоритм. Требования к алгоритмам. Понятие рекурсии. Рекурсивные функции. Простейшие рекурсивные функции. Операторы образования примитивно-рекурсивных и частично-рекурсивных функций. Тезис Чёрча. Разрешимые и перечислимые множества. Машина Тьюринга[5]*. Универсальная машина Тьюринга*. ([1, часть 8, кроме разд. III]; [3, § 14.1, 14.2]).
