Правила выполнения и оформления контрольных работ. Контрольная работа по дисциплине
Контрольная работа по дисциплине
«Математика» (2 семестр)
Контрольные работы
- В процессе изучения курса математики студент должен выполнить ряд контрольных работ, главная цель которых – оказать студенту помощь в изучении дисциплины. Рецензии на эти работы позволяют студенту судить о степени усвоения им соответствующего раздела курса; указывают на имеющиеся у него пробелы, на желательное направление дальнейшей работы; помогают сформулировать вопросы для постановки их перед преподавателем.
- Не следует приступать к выполнению контрольного задания, не решив достаточного количества задач по материалу, соответствующему этому заданию. Опыт показывает, что чаще всего неумение решить ту или иную задачу контрольного задания вызывается тем, что студент не выполнил это требование.
- Контрольные работы должны выполняться самостоятельно. Несамостоятельно выполненная работа не даёт возможности преподавателю – рецензенту указать студенту на недостатки в его работе, в усвоении им учебного материала, в результате чего студент не приобретает необходимых знаний и может оказаться не подготовленным к зачёту и экзамену.
- Без предъявления прорецензированных контрольных работ студент не допускается к сдаче зачета и экзамена.
Правила выполнения и оформления контрольных работ
При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.
Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля для замечаний рецензента.
Номер варианта контрольной работы определяется как сумма двух последних цифр шифра (номера зачетной книжки).
- В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), название дисциплины, номе контрольной работы; здесь же следует указать название учебного заведения, дату отсылки работы в институт и адрес студента. В конце работы следует поставить дату её выполнения и подпись студента.
- В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту. Контрольные работы, содержащие не все задачи задания, а так же задачи не своего варианта, не зачитываются.
- Решение задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номера задач.
- Предрешением каждой задачи надо полностью выписать её условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеет общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера. Например, условие задачи 1 должно быть переписано так:
Даны векторы а(1;2;3), b(-1;3;2), c(7;-3;5), d(6;10;17) в некотором базисе. Показать…и т.д.
- Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
- После получения прорецензированной работы, как не зачтённой так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочёты и выполнить все рекомендации рецензента.
Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок.
В случае незачёта работы и отсутствия прямого указания рецензента о том, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.
Тематический план дисциплины 2 семестр
| № тем | Наименование тем и содержание разделов | |
| Неопределенный интеграл Определенный интеграл и его приложения | ||
| 1.1 | Понятие первообразной. Существование первообразной у непрерывной функции. Основная теорема о первообразной. Понятие неопределенного интеграла и его св-ва. Таблица неопределенных интегралов. | |
| 1.2 | Методы интегрирования. Основные классы интегрируемых функций. Интегрирование рациональных дробей. Понятие об эллиптических интегралах. Определенный интеграл. | |
| 1.3 | Задачи, приводящие к понятию определенного интеграла, определенный интеграл и его свойства. Оценка определенного интеграла, теорема о среднем, формула Ньютона-Лейбница. | |
| Обыкновенные дифференциальные уравнения | ||
| 2.1 | Задачи, приводящие к дифференциальным уравнениям. Общие определения. Дифференциальные уравнения первого порядка, геометрический смысл, теорема существования и единственности решения, Основные типы дифференциальных уравнений первого порядка. Особые решения. | |
| 2.2 | Дифференциальные уравнения второго порядка. Основные понятия, теорема существования и единственности решения. Уравнения, допускающие понижение порядка. | |
| 2.3 | Линейные дифференциальные уравнения второго порядка, определение и общие свойства, теоремы о структурах общих решений однородного и неоднородного уравнений. Метод вариаций произвольных постоянных. | |
| Ряды | ||
| 3.1 | Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости. Ряды с положительными членами. Интегральный признак Коши. | |
| 3.2 | Достаточные признаки сходимости рядов с положительными членами. Признак Даламбера, радикальный признак Коши. Признак сравнения. | |
| 3.3 | Ряды с произвольными членами. Признак Лейбница. Абсолютная сходимость. | |
| 3.4 | Функциональные ряды. Общие определения. Степенные ряды. Теорема Абеля. Область сходимости. | |
| 3.5 | Разложение функций в степенные ряды, применение степенных рядов в приближенных вычислениях. | |
| Элементы теории вероятностей | ||
| 4.1 | Случайные события. Классическое определение вероятности. Операции над событиями. Теоремы о вероятности суммы и произведения. Полная вероятность. Схема повторных независимых испытаний Бернулли. | |
| 4.2 | Случайные величины. Числовые характеристики. Основные законы распределений. | |
| 4.3 | Критическая область. Проверка гипотез. | |
| 4.4 | Статистическая обработка результатов наблюдений. |
Контрольная работа №3
Задание 1.Найти интегралы, используя табличные формулы
и свойство линейности:
Вариант 1. А. 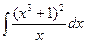 Б.
Б. 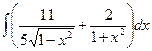 .
.
Вариант 2. А. 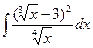 Б.
Б. 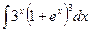 .
.
Вариант 3. А. 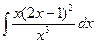 Б.
Б. 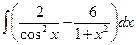 .
.
Вариант 4. А. 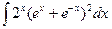 Б.
Б. 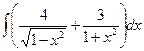 .
.
Вариант 5. А. 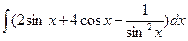 Б.
Б. 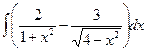 .
.
Вариант 6. А. 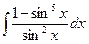 Б.
Б. 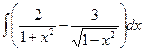 .
.
Вариант 7. А. 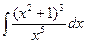 Б.
Б. 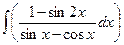 .
.
Вариант 8. А. 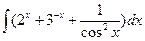 Б.
Б. 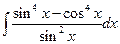 .
.
Вариант 9. А. 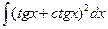 Б.
Б. 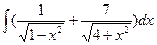 .
.
Вариант 10. А. 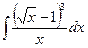 Б.
Б. 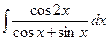 .
.
Вариант 11. А. 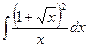 Б.
Б. 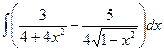 .
.
Вариант 12. А. 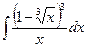 Б.
Б. 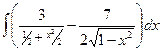 .
.
Вариант 13. А. 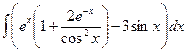 Б.
Б. 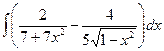 .
.
Вариант 14. А. 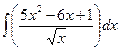 Б.
Б. 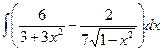 .
.
Вариант 15. А. 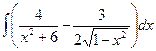 Б.
Б. 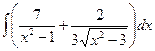 .
.
Вариант 16. А. 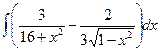 Б.
Б. 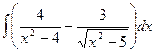 .
.
Вариант 17. А. 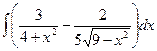 Б.
Б. 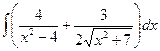 .
.
Вариант 18. А. 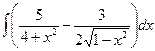 Б.
Б. 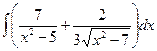 .
.
Вариант 19. А. 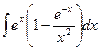 Б.
Б. 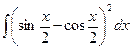 .
.
Вариант 20. А. 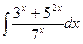 Б.
Б. 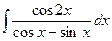 .
.
Задание 2. Найти интегралы методом подстановки:
Вариант 1. А. 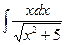 Б.
Б. 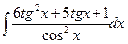 .
.
Вариант 2. А. 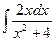 Б.
Б. 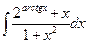 .
.
Вариант 3. А. 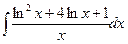 Б.
Б. 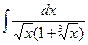 .
.
Вариант 4. А. 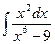 Б.
Б. 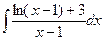 .
.
Вариант 5. А. 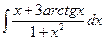 Б.
Б. 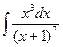
Вариант 6. А. 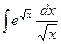 Б.
Б. 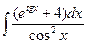 .
.
Вариант 7. А. 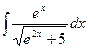 Б.
Б. 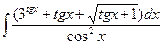 .
.
Вариант 8. А. 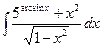 Б.
Б. 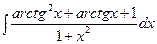 .
.
Вариант 9. А. 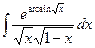 Б.
Б. 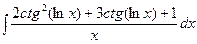 .
.
Вариант 10. А. 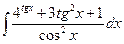 Б.
Б. 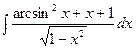 .
.
Вариант 11. А. 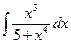 Б.
Б. 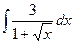 .
.
Вариант 12. А. 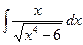 Б.
Б. 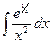 .
.
Вариант 13. А. 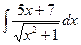 Б.
Б. 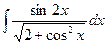 .
.
Вариант 14. А. 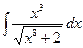 Б.
Б. 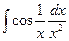 .
.
Вариант 15. А. 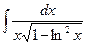 Б.
Б. 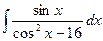 .
.
Вариант 16. А. 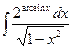 Б.
Б. 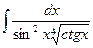 .
.
Вариант 17. А. 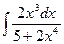 Б.
Б. 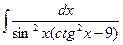 .
.
Вариант 18. А. 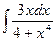 Б.
Б. 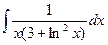 .
.
Вариант 19. А. 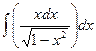 Б.
Б. 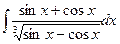 .
.
Вариант 20. А. 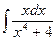 Б.
Б. 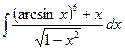 .
.
Задание 3.Выполнить интегрирование по частям:
Вариант 1. 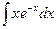 .
.
Вариант 2. 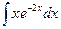 .
.
Вариант 3. 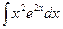 .
.
Вариант 4. 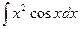 .
.
Вариант 5. 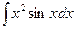 .
.
Вариант 6. 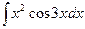 .
.
Вариант 7. 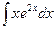 .
.
Вариант 8. 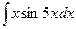 .
.
Вариант 9. 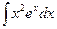 .
.
Вариант 10. 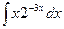 .
.
Вариант 11. 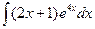 .
.
Вариант 12. 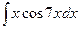 .
.
Вариант 13. 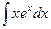 .
.
Вариант 14. 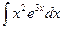 .
.
Вариант 15. 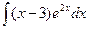 .
.
Вариант 16. 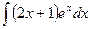 .
.
Вариант 17. 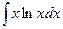 .
.
Вариант 18. 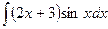 .
.
Вариант 19. 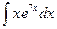 .
.
Вариант 20. 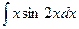 .
.
Задание 4.Найти площади фигур, ограниченных линиями.
Вариант 1. 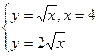
Вариант 2. 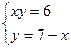
Вариант 3. 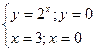
Вариант 4. 
Вариант 5. 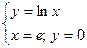
Вариант 6. 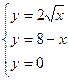
Вариант 7. 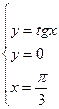
Вариант 8. 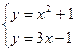
Вариант 9. 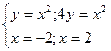
Вариант 10. 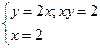
Вариант 11. 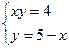
Вариант 12. 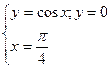
Вариант 13. 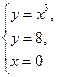
Вариант 14. 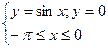
Вариант 15. 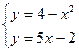
Вариант 16. 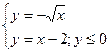
Вариант 17. 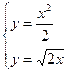
Вариант 18. 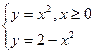
Вариант 19. 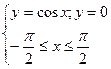
Вариант 20. 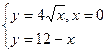
Задание 5.Решить обыкновенные дифференциальные уравнения:
Вариант 1. А. 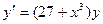 ; Б.
; Б. 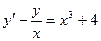 ;
;
Вариант 2. А. 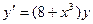 ; Б.
; Б. 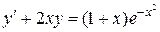 ;
;
Вариант 3. А. 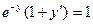 ; Б.
; Б. 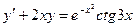 ;
;
Вариант 4. А. 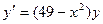 ; Б.
; Б. 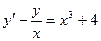 ;
;
Вариант 5. А. 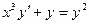 ; Б.
; Б. 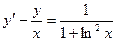 ;
;
Вариант 6. А. 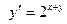 ; Б.
; Б. 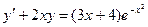 ;
;
Вариант 7. А. 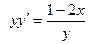 ; Б.
; Б. 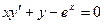 ;
;
Вариант 8. А. 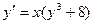 ; Б.
; Б. 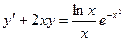 ;
;
Вариант 9. А. 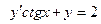 ; Б.
; Б. 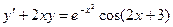 ;
;
Вариант10. А. 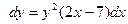 ; Б.
; Б. 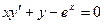 ;
;
Вариант11. А. 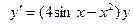 ; Б.
; Б. 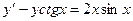 ;
;
Вариант12. А. 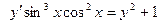 ; Б.
; Б. 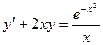 ;
;
Вариант13. А. 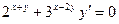 ; Б.
; Б. 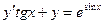 ;
;
Вариант14. А. 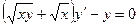 ; Б.
; Б. 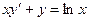 ;
;
Вариант15. А. 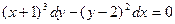 ; Б.
; Б. 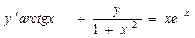 ;
;
Вариант 16. А. 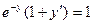 ; Б.
; Б. 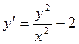 ;
;
Вариант 17. А. 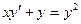 ; Б.
; Б. 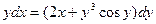 ;
;
Вариант 18. А. 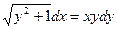 ; Б.
; Б. 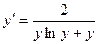 ;
;
Вариант 19. А. 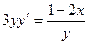 ; Б.
; Б. 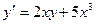 ;
;
Вариант 20. А. 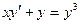 ; Б.
; Б. 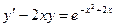 ;
;
Задание 6.Решить неоднородные линейные уравнения второго порядка:
1. А. 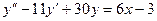 Б.
Б. 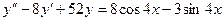 .
.
2. А. 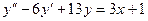 Б.
Б. 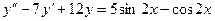 .
.
3. А. 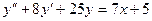 Б.
Б. 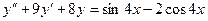 .
.
4. А. 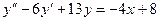 Б.
Б. 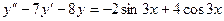 .
.
5. А. 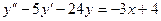 Б.
Б. 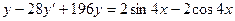 .
.
6. А. 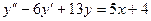 Б.
Б. 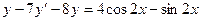 .
.
7. А. 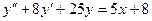 Б.
Б. 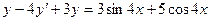 .
.
8. А. 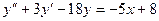 Б.
Б. 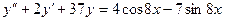 .
.
9. А. 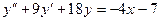 Б.
Б. 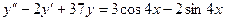 .
.
10. А. 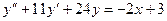 Б.
Б. 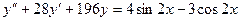 .
.
11. А. 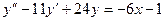 Б.
Б. 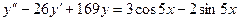 .
.
12. А. 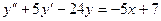 Б.
Б. 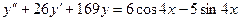 .
.
13. А. 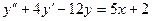 Б.
Б. 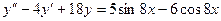 .
.
14. А. 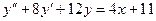 Б.
Б. 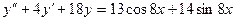 .
.
15. А. 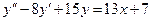 Б.
Б. 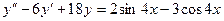 .
.
16. А. 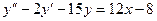 Б.
Б. 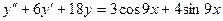 .
.
17. А. 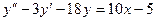 Б.
Б. 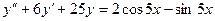 .
.
18. А. 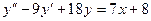 Б.
Б. 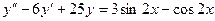 .
.
19. А. 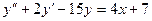 Б.
Б. 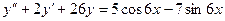 .
.
20. А. 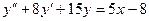 Б.
Б. 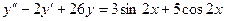 .
.
Контрольная работа №4
Задание 1.Исследовать на сходимость ряды с положительными членами:
Вариант 1. 1) 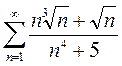 2)
2) 
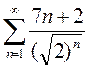 3)
3) 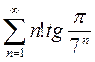
Вариант 2. 1) 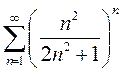 2)
2) 
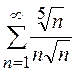 3)
3) 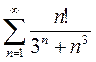
Вариант 3. 1) 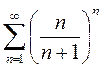 2)
2) 
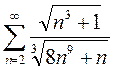 3)
3) 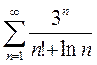
Вариант 4. 1) 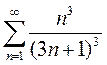 2)
2) 
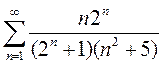 3)
3) 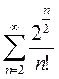
Вариант 5. 1) 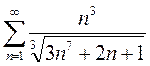 2)
2) 
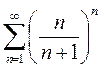 3)
3) 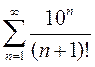
Вариант 6. 1) 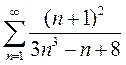 2)
2) 
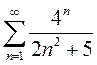 3)
3) 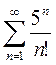
Вариант 7. 1) 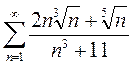 2)
2) 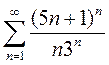 3)
3) 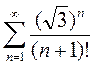
Вариант 8. 1) 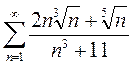 2)
2) 
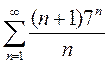 3)
3) 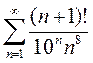
Вариант 9. 1) 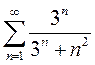 2)
2) 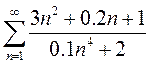 3)
3) 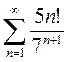
Вариант10. 1) 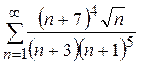 2)
2) 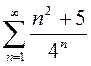 3)
3) 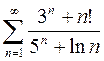
Вариант11. 1) 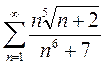 2)
2) 
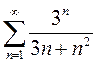 3)
3) 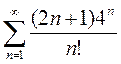
Вариант12. 1) 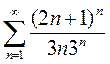 2)
2) 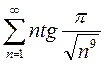 3)
3) 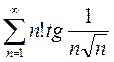
Вариант13. 1) 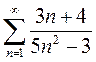 2)
2) 
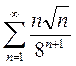 3)
3) 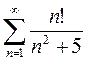
Вариант14. 1) 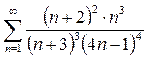 2)
2) 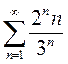 3)
3) 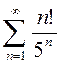
Вариант15. 1) 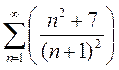 2)
2) 
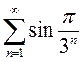 3)
3) 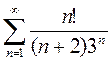
Вариант 16. 1) 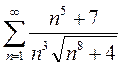 2)
2) 
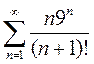 3)
3) 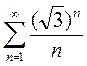
Вариант 17. 1) 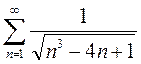 2)
2) 
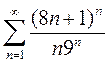 3)
3) 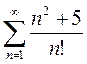
Вариант 18. 1) 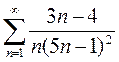 2)
2) 
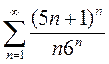 3)
3) 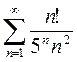
Вариант 19. 1) 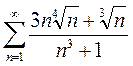 2)
2) 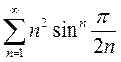 3)
3) 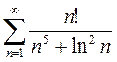
Вариант 20. 1) 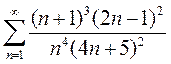 2)
2) 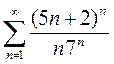 3)
3) 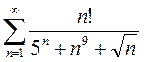
Задание 2.Найти область сходимости степенных рядов:
Вариант 1. 1) 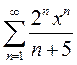 2)
2) 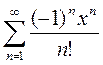
Вариант 2. 1) 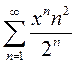 2)
2) 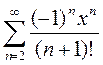
Вариант 3. 1) 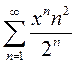 2)
2) 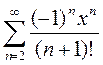
Вариант 4. 1) 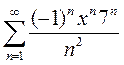 2)
2) 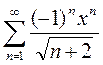
Вариант 5. 1) 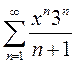 2)
2) 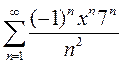
Вариант 6. 1) 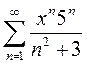 2)
2) 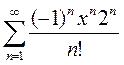
Вариант 7. 1) 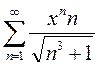 2)
2) 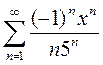
Вариант 8. 1) 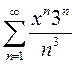 2)
2) 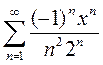
Вариант 9. 1) 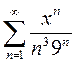 2)
2) 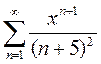
Вариант10. 1) 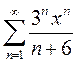 2)
2) 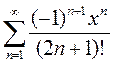
Вариант11. 1) 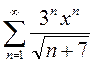 2)
2) 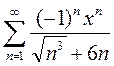
Вариант12. 1) 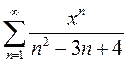 2)
2) 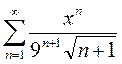
Вариант13. 1) 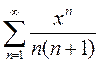 2)
2) 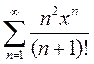
Вариант14. 1) 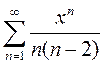 2)
2) 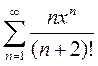
Вариант15. 1) 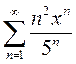 2)
2) 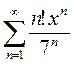
Вариант 16. 1) 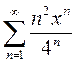 2)
2) 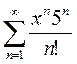
Вариант 17. 1) 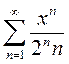 2)
2) 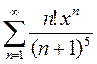
Вариант 18. 1) 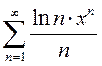 2)
2) 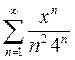
Вариант 19. 1) 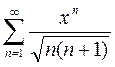 2)
2) 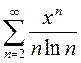
Вариант 20. 1) 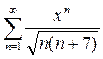 2)
2) 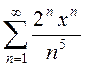
Задание №3
