Задания для выполнения самостоятельной работы

6.1. Задания для расчета балок на прочность

6.2.1. Задачи на прочность

6.2. Задачи для расчета балок на прочность

6.3. Задания для расчета балок на жесткость

7. Основные размеры двутавровых балок

8. Пример расчета консольной балки на прочность

Пример 8.1.

20,86 aM P P q aq ap 2,4 l=3,0 A II I III M M A 1,2 G RA RA MA x1 P P x2 x3 B x03 ­ ­ RA MA ЭQ,кН ЭMи,кН·м 13,6 0,64 5,84 16,32 24,86 22,54 19,3 20,88 1,8 I AAAAIQB6pisG4AAAAAoBAAAPAAAAZHJzL2Rvd25yZXYueG1sTI/BTsMwEETvSPyDtUjcqNOG4jTE qQqoB8QFChVXN16SqPE6it02/fsuJziu9mnmTbEcXSeOOITWk4bpJAGBVHnbUq3h63N9l4EI0ZA1 nSfUcMYAy/L6qjC59Sf6wOMm1oJDKORGQxNjn0sZqgadCRPfI/Hvxw/ORD6HWtrBnDjcdXKWJA/S mZa4oTE9PjdY7TcHp2ERg3p/Ud697udvavWktvL8vdX69mZcPYKIOMY/GH71WR1Kdtr5A9kgOg1p Nl0wqmGmeAIDaZbeg9gxmcwzkGUh/08oLwAAAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADh AQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4 /SH/1gAAAJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQD/ rieOEQIAAEEEAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAA IQB6pisG4AAAAAoBAAAPAAAAAAAAAAAAAAAAAGsEAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQA BADzAAAAeAUAAAAA " strokecolor="black [3213]"/> 0,9 x y Рис. 12. Схема балки и эпюры Q и Mи.

Исходные данные. М = 4,0 кН·м, Р = -13,6кН, q = 10,8кН/м. l = 3,0 м, aм = 2,4 м, aр = 0 м, aq = 1,2 м.   Требуется: 1. Изобразить схему балки согласно числовым данным. 2. Определить реакции опор и построить эпюры Q и Mи. 3а. Выбрать № двутавра при = 160 Мпа (материал – сталь). 3б. Определить диаметр деревянной балки круглого сечения при = 10 Мпа. 3в. Определить размеры деревянной балки прямоугольного сечения при = 10 Мпа, если высота h, больше ширины b в два раза.   Решение. Определим равнодействующую G равномерно распределенной нагрузки (РРН).

G = q·l_1, где l₁ – длина участка балки на которую действует (РРН).

G = 10,8 · 1,8 = 19,44 кН.

1.Определение сил реакций в опорах.

= 0. P · 3 – G · 0,9 – M – M_A = 0

– + M_A = P · 3 – G · 0,9 – M = 13,6 · 3–19,44 · 0,9 –4 =

= 40,8 – 17,5 + 4 = 19,3 кН·м.

= 0. G · 2,1 – M + R_A · 3 – M_A = 0. R_A = =

= = – 5,83 кН.

Проверка. = 0. – P + G – R_A = 0.

– 13,6 + 19,44 – 5,83 = 0. 19,44 – 19,43 = 0. 0 = 0

2. Построение эпюр Q и M_и.

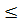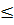I - й участок. 0 х₁ 1,2

Уравнение Q₁. Q₁ = – P = – 13,6 кН. Строим эпюру Q₁.

Уравнение M_и1. M_{и 1} = – P·х₁ = – 13,6·х₁. Это уравнение прямой линии. Её можно построить по двум точкам. х₁ = 0, M_{и 1} = 0

х₁ = 1,2 M_{и 1} = – 13,6·1,2 = – 16,32 кН·м. Строим эпюру M_{и 1}.

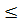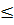II - й участок. 1,2 х₂ 2,4

Уравнение Q₂ . Q₂ = –P+G₂ = – 13,6 + q(х₂ – 1,2) = – 13,6 + 10,8(х₂ – 1,2).

х₂ = 1,2 Q₂ = –13.6 + 10,8 ·0 = –13.6 кН.

х₂ = 2,4 Q₂ = –13.6 + 10,8 ·1,2 = –0,64 кН. Строим эпюру Q₂.

Уравнение M_{и 2}. M_{и 2} = –P· х₂ + q = –13,6·х₂ + q . Это уравнение параболы. Параболу можно построить как минимум по трем точкам. х₂ = 1,2 M_{и 2} = –13,6·1,2 + 10,8 = – 16,32 кН·м.

х₂ = 2,4 M_{и 2} = –13,6·2,4+10,8 = –31,64 + 10,8 =

–31,64 + 7,77= –24,86 кН·м. В качестве 3 –й точки возьмем точку расположенную в центре второго участка.

х₂ = a_q + = 1,2 + = 1,2 + 0,6 = 1,8 м.

M_{и 2} = –13,6·1,8+10,8 = –24,48+ = –24,48+1,944= –22,54 кН·м.

По 3-м точкам строим эпюру M_{и 2}.

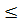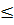III - й участок. 0 х₃ 0,6

Уравнение Q₃. Q₃ = R_A – G₃ = 5,83– q · х₃. х₃ = 0, Q₃ = 5,83кН.

х₃ = 0.6, Q₃ = 5,83 – 10,8· 0,6 = 5,83 – 6,48 = – 0,65кН. Строим эпюру Q₃.

Эпюра Q₃ показывает, что на 3-м участке есть точка в которой поперечная сила равна нулю. Надо расчитать расстояние х₃ до этой точки. Для этого приравняем уравнение Q₃ нулю. 0 = 5,83– 10,8· х₃. х₀₃ = = 0,54 м.

Уравнение M_{и 3}. M_{и 3} = –R_A х₃ – M_A + G₃ = –5,84 х₃ – 19,3 + q =

– 5,84 х₃ – 19,3 +10,8 . х₃ = 0, M_{и 3} = – 19,3 кН·м.

х₃ = 0,6, M_{и 3} = – 5,84·0,6– 19,3 +10,8 = – 22,8 + 1,94 = – 20,86 кН·м.

х₃ = 0,54, M_{и 3} = – 5,84· 0,54– 19,3 +10,8 =

= – 3,15 – 19,3 + 1,57 = – 20,88 кН·м. Cтроим эпюру M_и .

После тго как эпюры будут построены, надо провести их анализ. Эпюры Q и M_и должны соответствовать следующим требованиям.

а) на участке, где поперечная сила имеет знак «+», эпюра M_и слева на право возрастает, и наоборот;

б) скачок на эпюре Q возникает в том сечении, к которому приложена внешняя сила, в том числе сила реакции. Скачок равен величине прикладываемой силы;

в) скачок на эпюре M_и возникает в том сечении, к которому приложен внешний момент. Скачок равен этому моменту;

г) на участке, где приложена равномерно распределенная нагрузка (РРН), эпюра M_и имеет вид параболы. Выпуклость параболы направлена навстречу стрелочкам РРН;

д) в сечении, где Q = 0, эпюра M_и имеет экстремум (минимальное или максимальное значение) на данном участке.

Построенные на рис. 12. эпюры, соответствуют перечисленным свойствам.

3. Выбор № двутавра и размеров поперечных сечений.

3.1. Номер двутавра выбирают по осевому моменту сопротиления W₀, которое находят из условия прочности при изгибе:

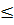
= , W₀ = .

В этом примере M_{и max} = 24,86 кН·м = 24860 · Н·мм.

W₀ = = 155, 37· мм³ = 155, 37 см³. По данному W₀ выбирается двутавр № 18а. Его осевой момент сопротивления

W₀ = 159,0 см³.

3.2. Для круглого поперечного сечения W₀ = 0,1d³. Для дерева = 10 МПа . Из условия прочности W₀ = = , отсюда d = = = 10 =

=10 = 10·29,37 = 293,7 мм.

3.3. Для прямоугольного сечения W₀ = , где b и h соответственно ширина и высота сечения. В примере h = 2 b.

W₀ = = = = .

b = = =10 =10·15,5= 155 мм.

h = 2 b = 2·155 = 310 мм.

9. Примеры расчета балок на жесткость

Пример 9.1.

ЭQ,кН ЭMи,кН·м y х аq2 аq1 аМ аР l = 4,6 M P A A C C B M P q q G x1 x2 x3 1,3 1,4 0,7 2,7 1,9 0,5l = 2,3 11,52 3,53 5,84 18,58ЭMи,кН·м 8,8 3,6 6,2 RA MA 13,0 14,0 10,0 12,6 1,92 5,6 ­ ­ ­ А(0) D (0,8) E(1,5) B(2,3) F(3,1) K(4,0) C(4,6) Рис. 13. Схема, эпюры и изогнутая ось балки.

Для данной схемы необходимо: 1. Определить силы реакций. 2. Построить эпюры поперечной силы Q и момента изгибающего Mи. 3. Подобрать № двутавра. 4. Используя универсальные уравнения упругой линии балки определить прогиб в точке С ( ) и в т. В, ( ). 5. Определив перемещения еще 4 – 5 точек построить изогнутую линию оси балки. Модуль упругости материала балки Е = 2·105 МПа. aq1 = 1,3 м, aq2 = 2,7 м, aP = 2,7 м, aM =4,6 м, l = 4,6 м, M = 8,8 кН·м, P = 6,2 кН, q = – 3,8 кН/м, = 145 МПа.

Решение.

Равнодействующая равномерно распределенной нагрузки

G = q· l₁ = 3,8·1,4 = 5,32 кН.

1.Определение опорных реакций.

= 0. – M_A + G · 2 + P· 2,7 – M = 0.

M_A = G · 2 + P· 2,7 – M = 5,32 · 2 + 6,2 · 2,7 – 8,8 = 18,58 кН·м.

= 0. – M_A + R_A· 4,6 – G · 2,6 – P · 1,9 – M = 0.

R_A = = = = 11,52 кН.

Проверка. = 0. – R_A + G + P = 0. – 11,52 + 5,32 + 6,2 = 0.

11,52 – 11,52 = 0. 0 = 0

2.Построение эпюр Q и M_и.

I – й участок. 0 х₁ 1,3

Уравнение Q₁. Q₁ = – R_A = – 11,52 кН. Строим эпюру Q₁.

Уравнение M_и1. M_и1 = M_A – R_A· х₁ = 18,58 – 11,52· х₁.

х₁ = 0; M_и1 = 18,58 кН·м.

х₁ = 1,3; M_и1 = 18,58 – 11,52· 1,3 = 3,6 кН·м. Строим эпюру M_и1.

II – й участок. 1,3 х₂ 2,7

Уравнение Q₂. Q₂= – R_A + G₂ = – 11,52 + q(х₂ – 1,3) =– 11,52 + 3,8(х₂ – 1,3).

х₂ = 1,3; Q₂ = – 11,52 кН. х₂ = 2,7; Q₂ = – 11,52+ 3,8(2,7– 1,3)= – 6,2 кН.

Строим эпюру Q₂.

Уравнение M_и2. M_и2 = M_A – R_A· х₂ + G₂· = 18,58 –11,52 · х₂ +

+ q(х₂ – 1,3) = 18,58 –11,52 · х₂+ 3,8 .

х₂ = 1,3; M_и2=18,58 –11,52 ·1,3+ 0 = 18,58 – 14,98 = 3,6 кН·м.

х₂ = 2,7; M_и2=18,58 –11,52 ·2,7 +3,8 =18,58 – 31,1+3,8 =

= –8,8 кН·м.

Параболу надо строить минимум по 3-м точкам. Третью точку лучше взять в центре второго участка.

х₂ = 2,0; M_и2=18,58 –11,52 ·2,0 +3,8 =18,58 – 23,04 + 3,8 · 0,245 =

= –4,46 + 0,931 = – 3,53 кН·м. Строим эпюру M_и2 .

III – й участок. 0 х₃ 1,9

Уравнение Q₃. Q₃ = 0.

Уравнение M_и3. M_и3 = – M = – 8,8 кН·м. В это уравнение не входит расстояние х₃ . График данного уравнения представляет собой прямую линию расположенную параллельно оси х на расстоянии – 8,8 кН·м.

3. Выбор № двутавра.

Номер двутавра выбирают по осевому моменту сопротиления W₀, которое расчитывают из условия прочности при изгибе:

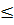
= , W₀ = .

В этом примере M_{и max} = 18,58 кН·м = 18 580 · Н·мм.

W₀ = = 128, 138· мм³ = 128, 138 см³. По данному W₀ выбирается двутавр № 18. Его осевой момент сопротивления

W₀ = 143,0 см³. Осевой момент инерции I = 1290 см⁴ .

4. Определение линейных перемещений.

Перемещения точек балки будем расчитывать используя универсальное уравнение (2), (см. стр. 22).

EI 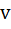= EI + EIθ₀ z + + + ,

4.1. Перемещение т.С. z = l = 4,6 м. Для консольной балки начало координат следует поместить в точку А. При этом θ₀ = 0, = 0.

EI = EI + EIθ₀ z + + + =

= M_A +M –R_A + P + q –q =

= 18,58 + 0 –11,52 +6,2 + 3,8 –3,8 =

= 18,58 ·10,58 –11,52 · 16,22 + 6,2 · 1,143 + 3,8 · 4,94 –3,8 · 0,543 =

=196,58 –186,88 + 7,08 + 18,78 –2,06 = 33,5 кН·м³ = 33,5 · 10³ Н·м³ .

Вычисляем жесткость материала –произведение EI.

E = 2 · 10⁵ МПа (Н/мм²) = 2 · 10² кН/мм² = 2 · 10⁸ кН/м² .

I = 1290 см⁴ = 1290 · 10^-8 м⁴.

EI = 2 · 10⁸ · 1290 · 10^-8 = 2580 кН·м² = 2580 · 10³ Н·м² .

= = 0,01298 м = 12,98 мм 13 мм.

4.2. Перемещение т. В. z = 2,3 м. θ₀ = 0, = 0.

EI = M_A – R_A + q = 18,58 · – 11,52 · +

+ 3,8 =18,58 · 2,645 – 11,52 · 2,03 + 3,8 · 0,0416 =

= 49,144 – 23,36 + 0,158 = 25,942 кН·м³ = 25,942 · 10³ Н·м³ .

= = 0,01005 м = 10,05 мм.

4.3. Перемещение т. К. z = 4,0 м. θ₀ = 0, = 0.

EI = M_A – R_A + q – q =

= 18,58 · – 11,52 + 6,2 + 3,8 – 3,8 =

= 18,58 ·8 – 11,52 · 10,66 + 6,2 ·0,366 + 3,8 · 2,214 – 3,8 · 0,119 =

= 148,64 – 122,8 + 2,269 + 8,413 – 0,452 = 36,07 кН·м³ = 36,07·10³ Н·м³ .

= = 0,01398 м = 13,98 мм 14 мм.

4.4. Перемещение т. F. z = 3,1 м. θ₀ = 0, = 0.

EI = M_A – R_A + q – q =

= 18,58 – 11,52 + 6,2 + 3,8 – 3,8 =

=89,28 – 57,2 + 0,062 + 0,425 – 0,004 = 32,563 кН·м³ = 32,563 · 10³ Н·м³.

= = 0,0126 м = 12,6 мм.

4.5. Перемещение т. E. z = 1,5 м. θ₀ = 0, = 0.

EI = M_A – R_A q =

=18,58 – 11,52 + 3,8 = 20,9 – 6,48 + 0,00025 = 14,42 кН·м³ =

= 14,42 · 10³ Н·м³. = = 0,00559 м = 5,6 мм.

4.6. Перемещение т. D. z = 0,8 м. θ₀ = 0, = 0.

EI = M_A – R_A = 18,58 – 11,52 =5,945 – 0,983 = =4,962 кН·м³ = 4,962 · 10³ Н·м³. = = 0,00192 м = 1,92 мм.

По вычисленным перемещениям построена изогнутая ось балки.

9.2. Расчет на жесткость балки опирающейся на две опоры.

q · C B C x2 A P M RA RB P M A B aP aM aq1 aq2 l=4,8 2,4 1,3 1,5 2,8 2,0 x1 x3 0,75 G ЭQ,кН ЭMи,кН·м x02 20,06 3,26 14,74 29,48 26,52 26,08 17,47 ­ ­ ­ l,м A(0) D(0,8) E(1,6) C(2,4) K(3,2) M(4,0) B(4,8) 12,0 6,42 10,8 10,4 5,93 Рис. 14. Схема, эпюры и перемещения балки.

Для данной схемы необходимо: 1. Определить силы реакций. 2. Построить эпюры поперечной силы Q и момента изгибающего Mи. 3. Подобрать № двутавра. 4. Используя универсальные уравнения упругой линии балки определить прогиб в центре балки, в т. С ( ). 5. Определив перемещения еще 4 – 5 точек построить изогнутую линию оси балки. Модуль упругости материала балки Е = 2·105 МПа. aq1 = 1,3 м, aq2 = 2,8 м, aP = 1,3 м, aM =2,8 м, l = 4,8 м, M = 12 кН·м, P = – 16,8 кН, q = 12 кН/м, = 140 МПа.

Решение.

Равнодействующая G = q· l₁ = 12 · 1,5 = 18 кН.

1.Определение сил реакций.

= 0. – P · 1,3 – G · 2,05 – M + R_B · 4,8 = 0.

R_B = = = = =14,74 кН.

= 0. – R_A · 1,3 + P · 3,5 + G · 2,75 – M = 0.

R_A = = = = = 20,06 кН.

Проверка. = 0. R_A – P – G + R_B = 0.

20,6 – 16,8 – 18 + 14,74 = 0. 34,8 – 34,8 = 0. 0 = 0.

2.Построение эпюр Q и M_и.

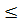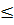I - й участок, 0 х₁ 1,3

Уравнение Q₁. Q₁ = R_A = 20,06 кН.

Уравнение M_и1. M_и1 = R_A · х₁ = 20,06 · х₁. х₁ = 0, M_и1 = 0.

х₁ = 1,3, M_и1 = 20,06 · 1,3 = 26,08 кН·м.

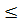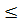II - й участок, 1,3 х₂ 2,8.

Уравнение Q₂. Q₂ = R_A – P – q(х₂ – 1,3) = 20,06 – 16,8 – 12(х₂ – 1,3) =

= 3,26 – 12(х₂ – 1,3). х₂ = 1,3, Q₂ = 3,26 кН.

х₂ = 2,8, Q₂ = 3,26 – 12(2,8 – 1,3) = 3,26 – 18 = – 14,74 кН. На 2-м участке есть точка, в которой Q₂ = 0. Надо определить расстояние х₀₂ от края балки до данной точки. Q₂ = 3,26 – 12(х₂ – 1,3) = 0, 3,26 – 12 х₂ + 15,6 = 0,

18,86 – 12 х₀₂ = 0, х₀₂ = = 1,57 м.

Уравнение M_и2. M_и2 = R_A · х₂ – P(х₂ – 1,3) –G₂ =

= 20,06·х₂ –16,8(х₂ –1,3) – q = 20,06· х₂ –16,8(х₂ –1,3) –12 .

х₂ = 1,3, M_и2 = 20,06·1,3 = 26,08 кН·м.

х₂ = 2,8, M_и2 = 20,06·2,8–16,8(2,8 –1,3) –12 = 56,168 – 25,2 – 13,5 =

= 17, 468 кН·м.

х₂ = 1,57, M_и2 = 20,06·1,57–16,8(1,57 –1,3) –12 = 31,49 – 4,536 –

– 0,437 = 26,52 кН·м.

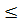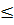III - й участок, 0 х₃ 2,0

Уравнение Q₃. Q₃ = – R_B = – 14,74 кН.

Уравнение M_и3. M_и3 = R_B· х₃ = 14,74· х₃. х₃ = 0, M_и3 = 0.

х₃ = 2,0, M_и3 = 14,74·2,0 = 29,48 кН·м.

3. Выбор двутавра.

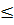
Условие прочности: = , отсюда W₀ = .

M_{и max} = 29,48 кН·м = 29480·10³ Н·мм. W₀ = = 210,57·10³ мм³ =

= 210,57 см³.

Выбирается двутавр № 22. W₀ = 232 см³, I = 2550 см⁴ = 2550·10^-8 м⁴.

4. Определение перемещений.

При определении перемещений будем использовать универсальные уравнения изогнутой оси балки.

EIθ = EIθ₀ + + , (1)

EI = EI + EIθ₀ z + + + , (2)

За начало координат принимается т. А. В этом случае известен один из параметров = = 0, так как на опоре прогиб отсутствует. Для определения линейного перемещения любой точки надо знать угол поворота крайнего левого сечения θ₀. Этот угол находят из уравнения (2) при расчете перемещения точки В, заранее зная, что оно равно нулю. При z = 4,8м имеем.

EIθ = EIθ₀ z +M +R_A – P – q + q =

EIθ₀·4,8 +12 + 20,06 – 16,8 – 12 + 12 =

EIθ₀·4,8 + 12 · 2 + 20,06 · 18,432 – 16,8·7,146 – 12· 6,25 +12· 0,666 =

EIθ₀·4,8 +24 +369,7 –120 – 75 + 8,0 = EIθ₀·4,8 + 206,7 = 0

EIθ₀·4,8 = – 206,7 кН·м³ = – 206,7·10³ Н·м³.

Определение жесткости материала балки EI.

Е = 2 · 10⁵ МПа (Н/мм²) = 2· 10¹¹ Па (Н/м²). I = 2550· 10^-8 м⁴.

EI = 2· 10¹¹ · 2550· 10^-8 = 5100 · 10³ Н·м².

θ₀ = θ_A = – = – = – = – 8,44· 10^-3 рад. · 57,3⁰ = – 0,484⁰.

Знак минус показывает, что поперечное сечение на левой опоре поворачивается по часовой стрелке.

4.1.Перемещение т. С. z = 2,4 м.

EIθ = EIθ₀ z +R_A – P – q =

EI · 2,4 + 20,06 – 16,8 – 12 = – 43,06· 2,4 +

+ 20,06·2,304 – 16,8 · 0,22 – 12 · 0,06 = –103,344 + 46,218 –3,696 – 0,72 =

= – 61,542 кН · м³ = – 61,542· 10³ Н · м³.

= – 0,012 м = – 12 мм.

4.2. Перемещение т. D. z = 0,8 м.

EIθ = EIθ₀ z +R_A = EI 0,8 + 20,06 = – 34,448 + 1,712 =

= – 32,736 кН·м³ = – 32,736 · 10³ Н ·м³.

= – 0,00642 м = – 6,42 мм.

4.3. Перемещение т. Е. z = 1,6 м.

EIθ = EIθ₀ z +R_A – P – q =

EI ·1,6 + 20,06 –16,8 –12 = – 68,896+13,694 –0,076–0,004 =

=13,694 – 68,976 = – 55,282 кН·м³ = – 55,282· 10³ Н ·м³.

= = – 0,0108 м = – 10,8 мм.

4.3. Перемещение т. К. z = 3,2 м.

EIθ = EIθ₀ z +M +R_A – P – q + q =

= EI ·3,2 + 12 + 20,06 – 16,8 – 12 + 12 =

= – 137,792 + 0,96 +109,554 – 19,205 – 6,516 + 0,0013 =

= 110,527 – 163,513 = – 52,986 кН·м³ = – 52,986 · 10³ Н ·м³.

= = – 0,0104 м = – 10,4 мм.

4.4. Перемещение т. М. z = 4,0 м.

EIθ = EIθ₀ z +M +R_A – P – q + q =

EI ·4 + 12 + 20,06 – 16,8 – 12 + 12 =

– 172,24 +8,64 +213,97 – 55,11 –26,57 + 1,07 = 223,68 – 253,92 =

= – 30,24 кН·м³ = – 30,24 · 10³ Н ·м³.

= = – 0,00593 м = – 5,93 мм.

По найденным значениям линейных перемещений построена изогнутая линия оси балки.

Литература

1. Степин П.А. Сопротивление материалов. - – СПб.:Лань,2014.- Режим

Доступа: http://e.lanbook.com

2. Миролюбов И.Н., Алмаметов Ф.З., Курицин Н.А., Изотопов И.Н.

Сопротивление материалов. Пособие по решению задач. – СПб.:Лань,2014.-

Режим доступа: http://e.lanbook.com

3. Кудрявцев С.Г., Сердюков В.Н. Сопротивление материалов. Интернет-тестирование базовых знаний. СПб.: Лань,2013. – Режим доступа: http://e.lanbook.com

4. Гнатюк В.В., Соляник С.С. Внутренние силовые факторы. Учебное пособие для выполнения самостоятельной работы студентов по дисциплине «Сопротивление материалов». СПб. 2013.