Уравнения Лагранжа II рода (без вывода)

Уравнения Лагранжа второго рода представляют собой дифференциальные уравнения движения несвободной механической системы, составленные в обобщенных координатах.Рассматривается движение системы, состоящей из n материальных точек относительно инерциальной системы отсчета. Наложенные на систему h связей – голономные, удерживающие, нестационарные. Если связи неидеальные, то соответствующие им реакции следует добавить к действующим на систему активным силам.

Пусть система имеет s = 3n – h степеней свободы и ее положение определяется q₁, q₂,…, q_i,…, q_s обобщенными координатами, а радиус-вектор любой точки этой системы - формулой (2.11): .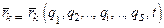

Виртуальноеперемещение k-й точки 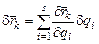, ее скорость

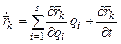. (2.19)

Уравнения Лагранжа второго рода формулируются следующим образом:

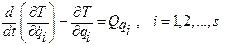, (2.20)

где T – кинетическаяэнергия механической системы; число уравнений Лагранжа II рода равно i = s числу степеней свободы системы; т.е. полная производная по времени d/dt от частной производной от кинетической энергии системы по обобщенной скорости 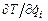минус частная производная от кинетической энергии системы по обобщенной координате 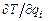равна обобщенной силе 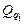, соответствующей обобщенной координате .

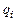В уравнения Лагранжа не входят заранее неизвестные реакции идеальных связей.

Если силы, действующие на систему, потенциальные, то обобщенные силы находятся по формуле (2.18), а уравнения Лагранжа второго рода в этом случае преобразуются к виду

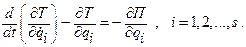(2.21)

Функция, равная разности кинетической и потенциальных энергий механической системы, называется функцией Лагранжа L = T – П. Так как потенциальная энергия системы является функцией только обобщенных координат, то

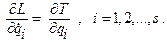
При использовании функции Лагранжа уравнения(2.21) принимают вид

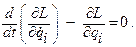(2.22)

Кинетическая энергия механической системы, состоящей из n материальных точек, как известно, определяется по формуле

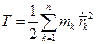. (2.23)

Принимая во внимание выражение (2.19), кинетическую энергию системы можно записать в виде

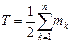
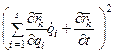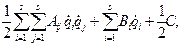= (2.24)

где

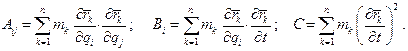
Если наложенные на систему связи стационарные, то 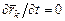, и тогда B_i = 0, C = 0. В этом случае кинетическая энергия системы является однородной квадратичной формой обобщенных скоростей:

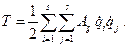(2.25)

Производные от кинетической энергии (2.25) по обобщенной скорости 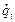и времени, соответствующие левой части уравнений Лагранжа второго рода (2.20), равны

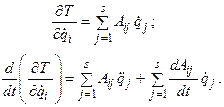
Так как 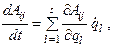то

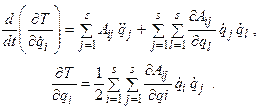
Подставляя эти выражения в уравнение Лагранжа (2.20), получаем

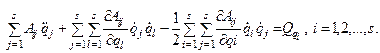(2.26)

Так как обобщенные силы - функции обобщенных координат, времени и, возможно, обобщенных скоростей, то каждое из уравнений (2.26) имеет второй порядок. Порядок уравнений не изменится и при нестационарных связях, так как в этом случае в выражения (2.26) войдут слагаемые, зависящие только от обобщенных координат, обобщенных скоростей и времени.

Таким образом, уравнения Лагранжа второго рода для механической системы с голономными связями представляют собой систему обыкновенных дифференциальных уравнений порядка 2n относительно обобщенных координат.

Уравнения Лагранжа второго рода сыграли решающую роль в развитии динамики систем и широко используются для решения многих задач динамики многопараметрических систем. Следует отметить, что для понимания существа и особенностей метода Лагранжа недостаточно изучения одной теории, необходимо рассматривать много примеров и задач. Изучение уравнений Лагранжа должно быть предметным.