Дифференциальные уравнения второго порядка
1) Линейные однородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами p и q называется уравнение вида
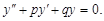 (8)
(8)
Алгебраическое уравнение k2 + pk + q = 0 называется характеристическим уравнением для данного дифференциального уравнения, а его корни – характеристическими числами (корнями).
Для нахождения общего решения уравнения (8):
1. Запишем соответствующее характеристическое уравнение
k2 + pk + q = 0.
2. В соответствии со знаком дискриминанта возможны три случая:
а) D > 0. Тогда характеристическое уравнение имеет два действительных корня k1 ¹ k2, и общее решение уравнения (8) имеет вид
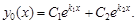 (9)
(9)
б) D = 0. Тогда k = k1 = k2 – действительный корень и общее решение уравнения (8) имеет вид
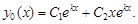 (10)
(10)
в) D < 0. Тогда корни k1, k2 – комплексно-сопряженные числа, т. е. k1, 2 = a ± ib, где a, b – действительные числа, и общее решение уравнения (8) имеет вид
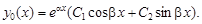 (11)
(11)
Отметим, что во всех перечисленных случаях С1, С2 – произвольные постоянные.
Пример 9. Найти общее решение дифференциальных уравнений:
1) 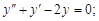
2) 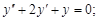
3) 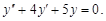
Решение
1. Запишем характеристическое уравнение k2 + k – 2 = 0.
Найдем его корни
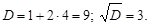
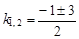 ; k1 = –2; k2 = 1.
; k1 = –2; k2 = 1.
Так как k1 ¹ k2 – действительные числа, то общее решение находим по формуле (9)
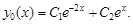
2. Запишем характеристическое уравнение k2 + 2k + 1 = 0.
Найдем его корни
k1 = k2 = –1.
В этом случае общее решение находим по формуле (10)
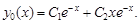
3. Запишем характеристическое уравнение k2 + 4k + 5 = 0.
Найдем его корни
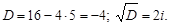
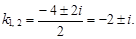 Здесь
Здесь 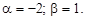
Общее решение находим по формуле (11)
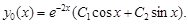
Тест 19. Однородным дифференциальным уравнением второго порядка с постоянными коэффициентами является уравнение вида:
1) 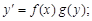
2) 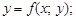
3) 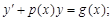
4) 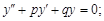
5) 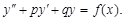
Тест 20. Однородным дифференциальным уравнением второго порядка с постоянными коэффициентами является:
1) 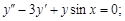
2) 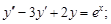
3) 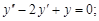
4) 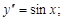
5) 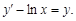
Тест 21. При решении однородного дифференциального уравнения второго порядка с постоянными коэффициентами 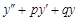 = 0:
= 0:
1) вводится подстановка вида y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции;
2) вводится подстановка вида y = u × x, где u = u(x) – некоторая неизвестная функция;
3) составляется характеристическое уравнение k2 + pk + q = 0.
Тест 22. Характеристическое уравнение k2 + pk + q = 0 имеет два различных действительных корня k1 и k2. Тогда общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 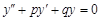 имеет вид:
имеет вид:
1) 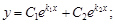
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3) 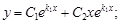
4) 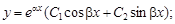
5) y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции.
Тест 23. Характеристическое уравнение k2 + pk + q = 0 имеет комплексные корни 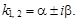 Тогда общее решение однородного диф-
Тогда общее решение однородного диф-
ференциального уравнения второго порядка с постоянными коэффициентами 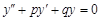 имеет вид:
имеет вид:
1) 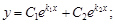
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3) 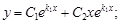
4) 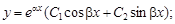
5) y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции.
Тест 24. Характеристическое уравнение k2 + pk + q = 0 имеет равные корни k1 = k2. Тогда общее решение однородного дифферен-
циального уравнения второго порядка с постоянными коэффициентами 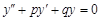 имеет вид:
имеет вид:
1) 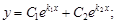
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3) 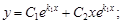
4) 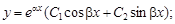
5) y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции.
Тест 25. Характеристическое уравнение k2 + pk + q = 0 имеет комплексные корни 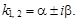 Тогда общее решение однородного диф-
Тогда общее решение однородного диф-
ференциального уравнения второго порядка с постоянными коэффициентами 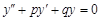 имеет вид:
имеет вид:
1) 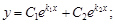
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3) 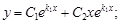
4) 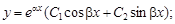
5) y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции.
Тест 26. Характеристическое уравнение k2 + pk + q = 0 имеет D = 0. Тогда общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 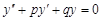 имеет вид:
имеет вид:
1) 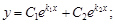
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3) 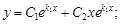
4) 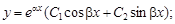
5) y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции.
Тест 27. Характеристическое уравнение k2 + pk + q = 0 имеет D < 0. Тогда общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 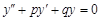 имеет вид:
имеет вид:
1) 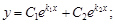
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3) 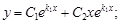
4) 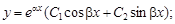
5) y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции.
Тест 28. Общее решение дифференциального уравнения
у¢¢ + 2у¢ + у = 0 находим по формуле:
1) 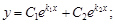
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3) 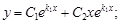
4) 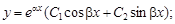
5) y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции.
Тест 29. Общее решение дифференциального уравнения
y¢¢ + 4y + 5y = 0 находим по формуле:
1) 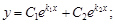
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3) 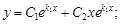
4) 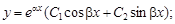
5) y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции.
Тест 30.Общим решением дифференциального уравнения 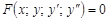 может являться функция:
может являться функция:
1) 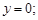
2) 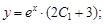
3) 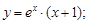
4) 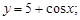
5) 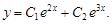
Ответы на тестовые задания
| Номер теста | ||||||||||||
| Правильный ответ |
2) Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
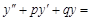 f(x), (12)
f(x), (12)
где p и q – постоянные;
функция f(x) – непрерывная.
Общее решение неоднородного уравнения можно представить в виде
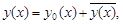
где y0(x) – общее решение соответствующего однородного уравнения;
yn(x) – частное решение неоднородного уравнения.
Тест 31. Линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами является уравнение вида:
1) 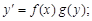
2) 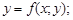
3) 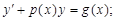
4) 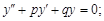
5) 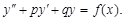
Тест 32.Линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами является уравнение вида:
1) 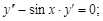
2) 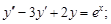
3) 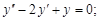
4) 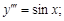
5) 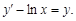
Тест 33.Общее решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами 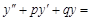 f(x) имеет вид:
f(x) имеет вид:
1) 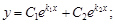
2) 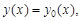 где
где 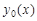 – общее решение соответствующего однородного уравнения;
– общее решение соответствующего однородного уравнения;
3) 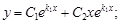
4) 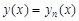 , где
, где 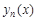 – частное решение неоднородного уравнения;
– частное решение неоднородного уравнения;
5) 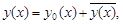 где
где  – общее решение соответствующего однородного уравнения,
– общее решение соответствующего однородного уравнения, 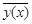 – частное решение неоднородного уравнения.
– частное решение неоднородного уравнения.
Несколько простейших случаев отыскания частных решений уравнения (12) приведены ниже.
1. Пусть в правой части уравнения (12) функция
f(x) 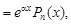 (13)
(13)
где 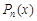 – многочлен степени n.
– многочлен степени n.
Тогда частное решение уравнения (12) будем искать в виде решений, приведенных в таблице 4.
Таблица 4
| Если a не является корнем соответствующего характеристического уравнения | Если a – корень характеристического уравнения кратности 1 | Если a – корень характеристического уравнения кратности 2 |
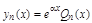 (14) (14) | 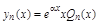 (15) (15) | 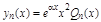 (16) (16) |
В равенствах 14–16 Qn(x) – многочлен степени n с неопределенными коэффициентами.
Напомним, что если n = 0, то Qn(x) = A; n = 1, то Qn(x) = Ax + B;
n = 2, то Qn(x) = Ax2 + Bx + C и т. д.
Пример 10. Определить вид частного решения уравнения
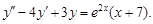
Решение
Запишем соответствующее однородное уравнение
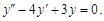
1. Характеристическое уравнение k2 – 4k + 3 = 0 имеет корни k1 = 1; k2 = 3.
2. В правой части данного уравнения функция вида (13)
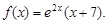
3. Здесь a = 2 – не является корнем характеристического уравнения; 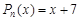 – многочлен первой степени.
– многочлен первой степени.
Следовательно, частное решение данного неоднородного уравнения надо искать в виде (14), т. е. 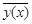 = e2x(Ax + B).
= e2x(Ax + B).
2. Пусть в правой части уравнения (12) функция
f(x) 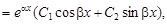 (17)
(17)
где C1 и C2 – постоянные.
Тогда частное решение уравнения (12) будем искать в виде решений, приведенных в таблице 5.
Таблица 5
| Если a ± bi не являются корнями соответствующего характеристического уравнения | Если a ± bi – корни характеристического уравнения |
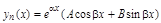 (18) (18) | 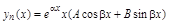 (19) (19) |
Пример 11. Определить вид частного решения уравнения
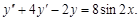
Решение
Запишем соответствующее однородное уравнение
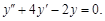
1. Характеристическое уравнение k2 + 4k – 2 = 0 имеет корни 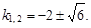
2. В правой части данного уравнения функция вида (17)
f(x) 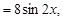 т. е. f(x)
т. е. f(x) 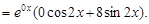
3. Здесь a = 0; b = 2. Составленные из этих значений комплексные числа a ± bi = 0 ± 2i не являются корнями характеристического уравнения.
Следовательно, частное решение данного неоднородного уравнения надо искать в виде (18), т. е. 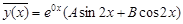 или
или 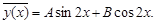
Тест 34. Характеристическое уравнение k2 – 4k + 3 = 0, соответ-
ствующее однородному дифференциальному уравнению второго порядка с постоянными коэффициентами 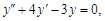 имеет корни k1 = 1; k2 = 3. Тогда частное решение соответствующего неоднородного уравнения
имеет корни k1 = 1; k2 = 3. Тогда частное решение соответствующего неоднородного уравнения 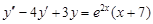 имеет вид:
имеет вид:
1) 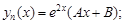
2) 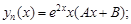
3) 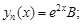
4) 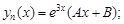
5) 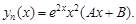
Тест 35. Характеристическое уравнение k2 – 4k + 4 = 0, соответ-
ствующее однородному дифференциальному уравнению второго порядка с постоянными коэффициентами 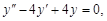 имеет корень k = 2. Тогда частное решение соответствующего неоднородного уравнения
имеет корень k = 2. Тогда частное решение соответствующего неоднородного уравнения 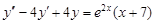 имеет вид:
имеет вид:
1) 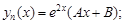
2) 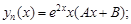
3) 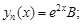
4) 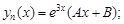
5) 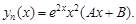
После того, как вид частного решения определен, методом неопределенных коэффициентов находим коэффициенты A и B.
Ответы на тестовые задания
| Номер теста | |||||
| Правильный ответ |
Ряды
Числовые ряды
Основные понятия
Пусть дана числовая последовательность 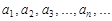 .
.
Выражение вида
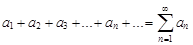 (1)
(1)
называется числовым рядом, или просто рядом.
Числа 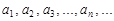 называются членами ряда, член an с произвольным номером – общим членом ряда.
называются членами ряда, член an с произвольным номером – общим членом ряда.
Суммы конечного числа членов ряда 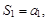
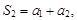
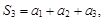 …,
…, 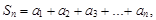 … называются частичными суммами ряда (1). Так как число членов ряда бесконечно, то частичные суммы ряда образуют бесконечную последовательность частичных сумм
… называются частичными суммами ряда (1). Так как число членов ряда бесконечно, то частичные суммы ряда образуют бесконечную последовательность частичных сумм
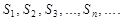 (2)
(2)
Пример 1. Пусть дана числовая последовательность
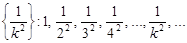 . (3)
. (3)
Тогда последовательность 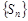 будет иметь вид
будет иметь вид
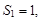
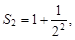
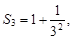 …,
…, 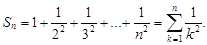
Последовательности (3) соответствует ряд
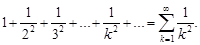 (4)
(4)
Пример 2.Рассмотрим ряд
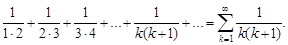 (5)
(5)
Найдем его частичную сумму Sn. Имеем
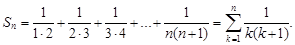
Его частичную сумму можно упростить, если заметить, что
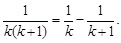
Получим
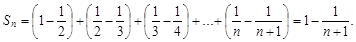
Тест 1. Определить второй член ряда 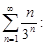
1) 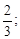
2) 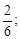
3) 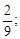
4) 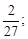
5) 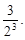
Ряд (1) называется сходящимся, если последовательность его частичных сумм (2) сходится к какому-нибудь числу S, которое называется суммой ряда (1). Символически
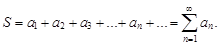
Если же последовательность частичных сумм (2) расходится, то ряд (1) называется расходящимся. Такой ряд суммы не имеет.
Тест 2.Определить частичную сумму S3 ряда 1 + 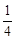 +
+ 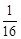 +
+ 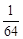 +… :
+… :
1) 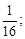
2) 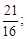
3) 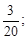
4) 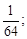
5) 3.
Простейшими примерами числовых рядов, вопрос о сходимости которых решен, являются следующие ряды:
1. 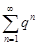 – геометрический ряд, который при
– геометрический ряд, который при 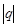 < 1 сходится, при
< 1 сходится, при 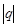 ≥ 1 расходится.
≥ 1 расходится.
2. 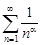 – обобщенный гармоничный ряд, который при α > 1 сходится, при α ≤ 1 расходится.
– обобщенный гармоничный ряд, который при α > 1 сходится, при α ≤ 1 расходится.
Пример 3.Исследовать сходимость ряда 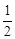 +
+ 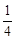 +
+ 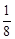 +…+
+…+ 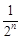 +… .
+… .
Решение
Это геометрический ряд, так как q = 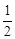 < 1, то ряд является сходящимся.
< 1, то ряд является сходящимся.
Тест 3. Указать, при каких значениях a обобщенный гармонический ряд является сходящимся:
1) при любых a;
2) при 0 < a< 1;
3) при a > 1;
4) при a≤ 1;
5) при 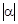 < 1.
< 1.
Тест 4. Для геометрического ряда 1+ 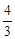 +
+ 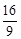 +
+ 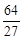 +… определить знаменатель q:
+… определить знаменатель q:
1) 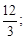
2) 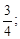
3) 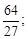
4) 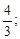
5) 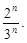
Факты сходимости и расходимости ряда устанавливаются с помощью признаков сходимости рядов, к рассмотрению которых и переходим.
