Гаусса-остроградского формула
Свойства криволинейного интеграла первого рода
Криволинейный интеграл I рода обладает следующими свойствами:
1. Интеграл не зависит от ориентации кривой;
2. Пусть кривая C1 начинается в точке A и заканчивается в точке B, а кривая C2 начинается в точкеB и заканчивается в точке D (рисунок 2). Тогда их объединением будет называться криваяC1 U C2, которая проходит от A к B вдоль кривой C1 и затем от B к D вдоль кривой C2. Для криволинейных интегралов первого рода справедливо соотношение
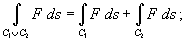
3. Если гладкая кривая C задана параметрически соотношением 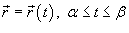 и скалярная функция F непрерывна на кривой C, то
и скалярная функция F непрерывна на кривой C, то
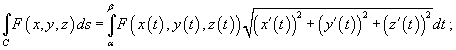
4. Если C является гладкой кривой в плоскости Oxy, заданной уравнением 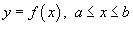 , то
, то
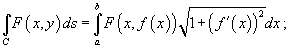
5. Если гладкая кривая C в плоскости Oxy определена уравнением 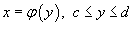 , то
, то
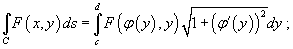
6. В полярных координатах интеграл 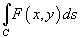 выражается формулой
выражается формулой
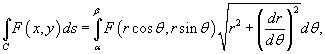
где кривая C задана в полярных координатах функцией 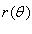 .
.
Криволинейный интеграл второго рода


Иллюстрация криволинейного интеграла второго рода на векторном поле
Править]Свойства
1. Линейность:
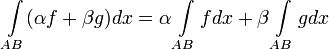
2. Аддитивность:
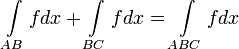
3. Монотонность: если 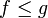 на
на  , то
, то
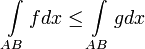
4. Оценка модуля:
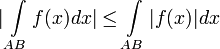
5. Теорема о среднем: если 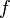 непрерывна на
непрерывна на 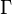 , то
, то 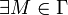 , такая что:
, такая что: 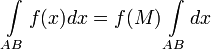
6. 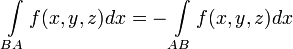
Править]Вычисление
Пусть  — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция
— гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция  определена и интегрируема вдоль кривой
определена и интегрируема вдоль кривой 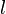 в смысле криволинейного интеграла второго рода. Тогда
в смысле криволинейного интеграла второго рода. Тогда
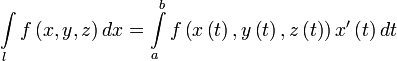 ,
,
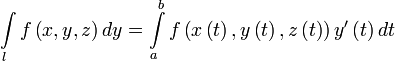 ,
,
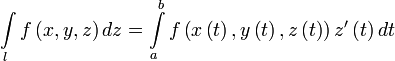 .
.
Если обозначить за 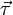 единичный вектор касательной к кривой
единичный вектор касательной к кривой 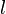 , то нетрудно показать, что
, то нетрудно показать, что
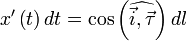
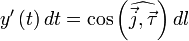
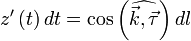
11) Замена переменных в двойном интеграле. Пусть функции 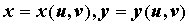 взаимно однозначно отображают открытое множество, содержащее область
взаимно однозначно отображают открытое множество, содержащее область 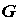 плоскости
плоскости 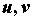 на открытое множество, содержащее область
на открытое множество, содержащее область 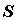 , и пусть
, и пусть 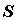 является образом
является образом 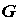 . Если
. Если 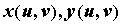 и их частные производные непрерывны, а определитель
и их частные производные непрерывны, а определитель 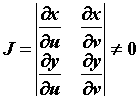 , то
, то 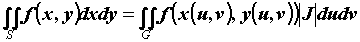 . Выражение
. Выражение 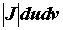 называется элементом площади в криволинейных координатах, функциональный определитель
называется элементом площади в криволинейных координатах, функциональный определитель 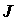 - якобианом.
- якобианом.
ПРИМЕР 1. Вычисление якобиана для полярных и обобщенных полярных координат.

Вычисление площади.
Замена переменных в тройном интеграле. Пусть посредством функций 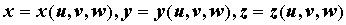 производится взаимно однозначное отображение открытого множества, содержащего область
производится взаимно однозначное отображение открытого множества, содержащего область 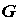 пространства
пространства 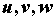 на открытое множество, содержащее область
на открытое множество, содержащее область 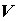 пространства
пространства 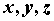 и
и 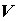 есть образ
есть образ 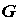 . Если эти три функции непрерывны вместе со своими первыми частными производными в области
. Если эти три функции непрерывны вместе со своими первыми частными производными в области 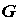 и якобиан
и якобиан 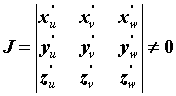 , то
, то 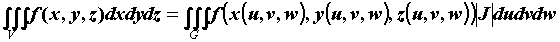 . Выражение
. Выражение 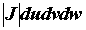 называется элементом объема в криволинейных координатах .
называется элементом объема в криволинейных координатах .
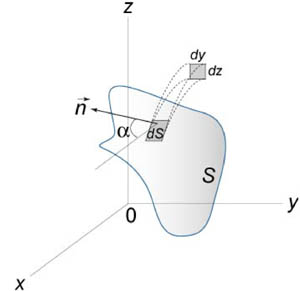
12) Поверхностный интеграл второго рода можно записать также в координатной форме. Пусть P (x,y,z), Q (x,y,z),R (x,y,z) являются компонентами векторного поля 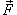 . Введем cos α, cos β, cos γ − направляющие косинусы внешней нормали
. Введем cos α, cos β, cos γ − направляющие косинусы внешней нормали  к поверхности S. Тогда скалярное произведение
к поверхности S. Тогда скалярное произведение 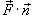 равно
равно
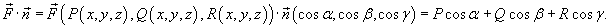
Следовательно, поверхностный интеграл можно записать в виде
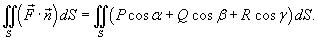
Поскольку 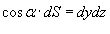 (рисунок 1), и, аналогично,
(рисунок 1), и, аналогично, 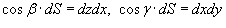 , получаем следующую формулу для вычисления поверхностного интеграла II рода:
, получаем следующую формулу для вычисления поверхностного интеграла II рода:
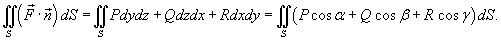
Если поверхность S задана в параметрической форме с помощью вектора 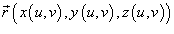 , то последняя формула принимает вид
, то последняя формула принимает вид
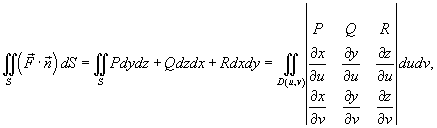
где (u,v) изменяются в пределах области интегрирования D(u,v).
 | ||
| Рис.1 |
Если поверхность S не представима в явном или параметрическом виде, то ее можно попробовать разбить на конечное число частей, каждая из которых представима в таком виде. В этом случае справедливо свойство аддитивности: поверхностный интеграл второго рода по поверхности S будет равен сумме интегралов по ее частям.
ГАУССА-ОСТРОГРАДСКОГО ФОРМУЛА
ГАУССА-ОСТРОГРАДСКОГО ФОРМУЛА
- одна из основных интегральных теорем векторного анализа, связывающая объемный интеграл с поверхностным:
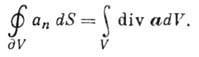
Здесь 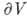 - замкнутая поверхность, ограничивающая 3-мерную область V, а п - проекция вектора
- замкнутая поверхность, ограничивающая 3-мерную область V, а п - проекция вектора 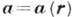 на внеш. нормаль к поверхности. Получена Дж. Грином (G. Green) и M. В. Остроградским в 1828, в частном случае К. Ф. Гауссом в 1813. Г.- О. ф. утверждает, что поток векторного поля через замкнутую поверхность (левая часть равенства) равен полной силе источников этого поля, заключённых внутри поверхности (правая часть). Из Г.- О. ф. следует, что поток поля, свободного от источников (т. е. такого, что
на внеш. нормаль к поверхности. Получена Дж. Грином (G. Green) и M. В. Остроградским в 1828, в частном случае К. Ф. Гауссом в 1813. Г.- О. ф. утверждает, что поток векторного поля через замкнутую поверхность (левая часть равенства) равен полной силе источников этого поля, заключённых внутри поверхности (правая часть). Из Г.- О. ф. следует, что поток поля, свободного от источников (т. е. такого, что 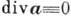 ), через любую замкнутую поверхность равен нулю. Г.- О. ф. и Стокса формула являются частными случаями теоремы Стокса, к-рая связывает между собой интегралы от дифференциальных форм разных размерностей. М. Б. Менский.
), через любую замкнутую поверхность равен нулю. Г.- О. ф. и Стокса формула являются частными случаями теоремы Стокса, к-рая связывает между собой интегралы от дифференциальных форм разных размерностей. М. Б. Менский.
14) Одним из частных случаев замены переменных является переход из декартовой в полярную систему координат (рисунок 1).
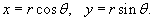
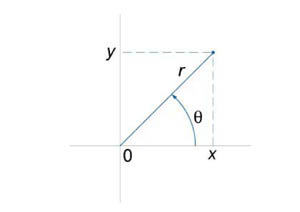 |  | |
| Рис.1 | Рис.2 |
Якобиан такого преобразования имеет вид
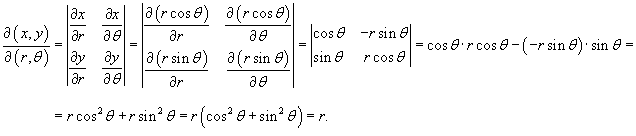
Следовательно, дифференциальный элемент в полярных координатах будет равен
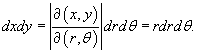
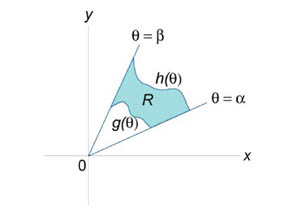
Пусть область интегрирования R в полярных координатах определяется следующим образом (рисунок 2):
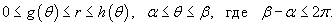
Тогда двойной интеграл в полярных координатах описывается формулой
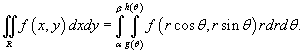
Будем называть полярным прямоугольником область интегрирования, показанную на рисунке 3 и удовлетворяющую условиям
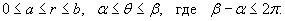
В этом случае формула замены переменных в двойном интеграле имеет вид
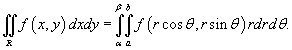
Будьте внимательны, чтобы не пропустить сомножитель (якобиан) r в правой части этой формулы!
 |  | |
| Рис.3 | Рис.4 |
15)
Поверхностный интеграл первого рода от функции 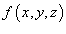 по поверхности S определяется следующим образом:
по поверхности S определяется следующим образом:
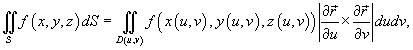
где частные производные 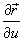 и
и 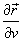 равны
равны
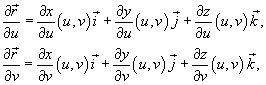
а 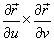 означает векторное произведение. Вектор
означает векторное произведение. Вектор 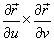 перпендикулярен поверхности в точке
перпендикулярен поверхности в точке 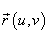 .
.
Абсолютное значение 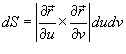 называется элементом площади: оно соответствует изменению площади dS в результате приращения координат u и v на малые значения du и dv (рисунок 1).
называется элементом площади: оно соответствует изменению площади dS в результате приращения координат u и v на малые значения du и dv (рисунок 1).
 |  | |
| Рис.1 | Рис.2 |
Числовые ряды
для него выполняются все условия признака сходимостиЛейбница.
Знакопеременные ряды
Рассмотрим числовые ряды
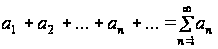 (5.1)
(5.1)
с произвольными членами, т. е. члены ряда могут быть как положительными, так и отрицательными. Такие ряды называются знакопеременными.
Образуем новый ряд, составленный из абсолютных величин (модулей) членов ряда (5.1), т. е. ряд
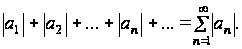 (5.2)
(5.2)
Теорема 5.1.Если ряд 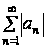 сходится, то сходится и исходный ряд
сходится, то сходится и исходный ряд 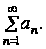
Вообще говоря, обратное утверждение неверно, т. е. из сходимости ряда (5.1) не следует сходимость ряда (5.2). Например, как было показано выше ряд 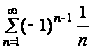 сходится, в то время как ряд
сходится, в то время как ряд 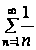 расходится.
расходится.
Определение 5.1.Ряд (5.1) называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов.
Определение 5.2.Сходящийся ряд (5.1) называется условно сходящимся, если ряд (5.2) расходится.
Таким образом, ряд 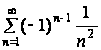 является абсолютно сходящимся.
является абсолютно сходящимся.
Абсолютно сходящиеся ряды обладают тем свойством, что у них можно любым образом менять местами члены ряда. При такой перестановке будут получаться также абсолютно сходящиеся ряды, при этом сумма ряда не изменяется. Как указывалось в разделе 2, условно сходящиеся ряды таким свойством не обладают.
17)
| Необходимый признак сходимости ряда |
Теорема. Если ряд сходится, то 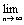 un=0. Доказательство. Пусть ряд u1+u2+…+un… сходится, то есть существует конечный предел un=0. Доказательство. Пусть ряд u1+u2+…+un… сходится, то есть существует конечный предел 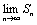 =S. Тогда имеет место также равенство =S. Тогда имеет место также равенство 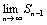 =S, так как при n =S, так как при n 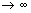 и (n-1) и (n-1) 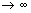 . Вычитая почленно из первого равенства второе, получаем . Вычитая почленно из первого равенства второе, получаем 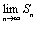 - - 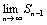 = = 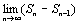 = = 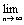 un=0, что и требовалось доказать. Следствие. Если un=0, что и требовалось доказать. Следствие. Если 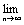 un≠0, то ряд u1+u2+…+un… расходится. Пример. Ряд un≠0, то ряд u1+u2+…+un… расходится. Пример. Ряд 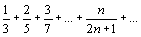 расходится, так как расходится, так как 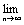 un= un= 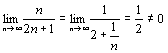 . Подчеркнём, что рассмотренный признак является только необходимым, но не достаточным, то есть из того, что . Подчеркнём, что рассмотренный признак является только необходимым, но не достаточным, то есть из того, что 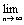 un=0 не следует, что ряд сходится. Позже докажем, что так называемый гармонический ряд un=0 не следует, что ряд сходится. Позже докажем, что так называемый гармонический ряд 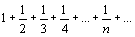 (6) расходится, хотя (6) расходится, хотя 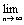 un= un= 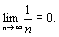 Этот ряд часто будет использоваться в дальнейшем. Этот ряд часто будет использоваться в дальнейшем. |
19) Интегральный признак Коши: Рассмотрим положительный числовой ряд 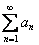 . Данный ряд сходится или расходится вместе с соответствующим несобственным интегралом.
. Данный ряд сходится или расходится вместе с соответствующим несобственным интегралом.
Пример 11
Исследовать ряд на сходимость 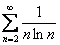
Почти классика. Натуральный логарифм и какая-нибудь бяка.
Основной предпосылкой использования интегрального признака Кошиявляется тот факт, что в общем члене ряда есть некоторая функция и её производная. Из темы Производная вы наверняка запомнили простейшую табличную вещь: 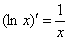 , и у нас как раз такой канонический случай.
, и у нас как раз такой канонический случай.
Как использовать интегральный признак? Сначала берем значок интеграла и переписываем со «счётчика» ряда верхний и нижний пределы: 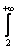 . Затем под интегралом переписываем «начинку» ряда с буковкой «хэ»:
. Затем под интегралом переписываем «начинку» ряда с буковкой «хэ»: 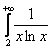 . Чего-то не хватает…, ах, да, еще в числителе нужно прилепить значок дифференциала:
. Чего-то не хватает…, ах, да, еще в числителе нужно прилепить значок дифференциала: 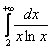 .
.
Теперь нужно вычислить несобственный интеграл 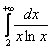 . При этом возможно два случая:
. При этом возможно два случая:
1) Если выяснится, что интеграл 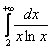
Признак Даламбера: Рассмотрим положительный числовой ряд 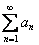 . Если существует предел отношения последующего члена к предыдущему:
. Если существует предел отношения последующего члена к предыдущему: 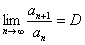 , то:
, то:
а) При 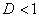 ряд сходится. В частности, ряд сходится при
ряд сходится. В частности, ряд сходится при 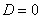 .
.
б) При 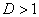 ряд расходится. В частности, ряд расходится при
ряд расходится. В частности, ряд расходится при 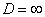 .
.
в) При 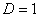 признак не дает ответа. Нужно использовать другой признак. Чаще всего единица получается в том случае, когда признак Даламбера пытаются применить там, где нужно использовать предельный признак сравнения.
признак не дает ответа. Нужно использовать другой признак. Чаще всего единица получается в том случае, когда признак Даламбера пытаются применить там, где нужно использовать предельный признак сравнения.
У кого до сих пор проблемы с пределами или недопонимание пределов, обратитесь к урокуПределы. Примеры решений
. Без понимания предела и умения раскрывать неопределенность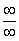 дальше, к сожалению, не продвинуться.
дальше, к сожалению, не продвинуться. А сейчас долгожданные примеры.
Пример 1
Исследовать ряд на сходимость 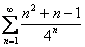
Мы видим, что в общем члене ряда у нас есть 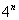 , а это верная предпосылка того, что нужно использовать признак Даламбера. Сначала полное решение и образец оформления, комментарии ниже.
, а это верная предпосылка того, что нужно использовать признак Даламбера. Сначала полное решение и образец оформления, комментарии ниже.
Используем признак Даламбера:

Таким образом, исследуемый ряд сходится.
21)Признак сравнения — утверждение об одновременности расходимости или сходимости двух рядов, основанный на сравнении членов этих рядов.
