Вектор-функция скалярного аргумента. Производная

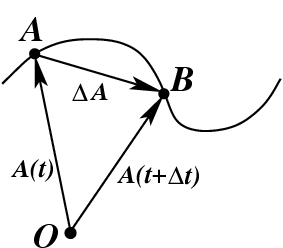
Пусть множество значений вектор-функции скалярного аргумента 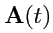приведено к общему началу в точке 0. Совместим с этой точкой начало декартовой системы координат. Тогда для любого 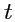вектор 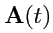может быть разложен по ортам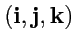

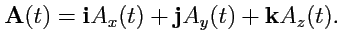
Таким образом, задание вектор-функции скалярного аргумента означает задание трех скалярных функций 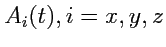При изменении значения аргумента конец вектора будет описывать в пространстве кривую, которая называется годографом вектора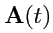

Пусть для 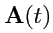существует близкое значение 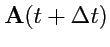Тогда производной вектор-функции поскалярному аргументу называется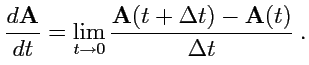

№17 Скорость и ускорение точки в криволинейном движении

Скорость

Скорость, вводится как характеристика движения материальной точки. Скорость является векторной величиной, которая характеризуется как быстротой движения (модуль вектора скорости), так и его направление (направление вектора скорости) в данный момент времени. Пусть материальная точка движется по какой-либо криволинейной траектории, при этом в момент времени t ей соответствует радиус-вектор r0 (рис. 1). За малый отрезок времени Δt точка совершит путь Δs и при этом получит элементарное (бесконечно малое) перемещение Δr.

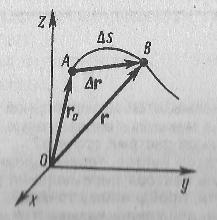
Рис.1

Вектором средней скорости <r> называется отношение приращения Δr радиуса-вектора точки к промежутку времени Δt:

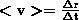(1)

Направление вектора средней скорости совпадает с направлением Δr. При бесконечном уменьшении Δt средняя скорость стремится к значению, которое называется мгновенной скоростью v:

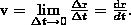
Значит, мгновенная скорость v есть векторная величина, которая равна первой производной радиуса-вектора движущейся точки по времени. Т.к. в пределе секущая совпадает с касательной, то вектор скорости v направлен по касательной к траектории в сторону движения (р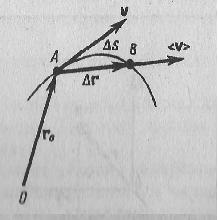ис. 2).

Рис.2

При уменьшении Δt, Δs все сильнее будет приближаться к |Δr|, поэтому модуль мгновенной скорости

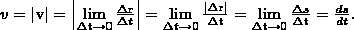
Значит, модуль мгновенной скорости равен первой производной пути по времени:

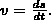(2)

При неравномерном движении модуль мгновенной скорости различен в разные моменты времени. В этом случае применяют скалярную величину <r> — среднюю скорость неравномерного движения:

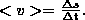
Если проинтегрировать по времени в пределах от t до t+Δt выражение ds=vdt (см. формулу (2)), то найдем длину пути, пройденного точкой за время Δt:

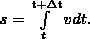(3)

В случае равномерного движения числовое значение мгновенной скорости постоянно; Toгда выражение (3) примет вид

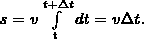
Длина пути, пройденного точкой за промежуток времени от t1 до t2, задается интегралом

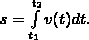
УСКОРЕНИЕ

При неравномерном движения частно необходимо знать, как быстро изменяется скорость с течением времени. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, называется ускорение. Рассмотрим плоское движение - движение, при котором траектории каждой точки рассматриваемой системы лежат в одной плоскости. Пусть вектор v есть скорость точки А в момент времени t. За время Δt точка перешла в положение В и получила скорость, отличную от v как по модулю, так и направлению и равную v1+Δv. Перенесем вектор v1 в точку А и найдем Δv (рис. 1).

Средним ускорением неравномерного движения в интервале от t до t+Δt называется векторная величина, равная отношению изменения скорости Δv к интервалу времени Δt:

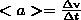
Мгновенным ускорением а (ускорением) материальной точки в момент времени t будет векторная величина:

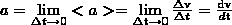
равная первой производной скорости по времени.

Разложим вектор Δv на две составляющие. Для этого из точки А (рис. 1) по направлению скорости v отложим вектор AD, по модулю равный v1. Очевидно, что вектор CD, равный Δvτ, определяет изменение скорости за время Δt по модулю : Δvτ=v1-v. Вторая же составляющая Δvn вектора Δv характеризует изменение скорости за время Δt по направлению.

Тангенциальная составляющая ускорения:

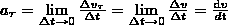
т. е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.

Ищем вторую составляющую ускорения. Допускаем, что точка В сильно близка к точке А, поэтому Δs можно считать дугой окружности некоторого радиуса r, слабо отличающейся от хорды АВ. Треугольников АОВ подобен треугольнику EAD, из чего следует Δvn/AB=v1/r, но так как AB=vΔt, то

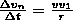
В пределе при Δt→0 получим v1→v.

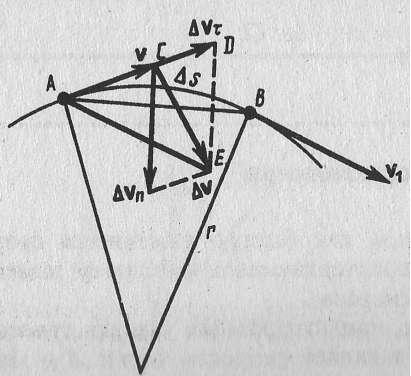
Рис.1

Т.к. v1→v, угол EAD стремится к нулю, а т.к. треугольник EAD равнобедренный, то угол ADE между v и Δvn стремится к прямому. Следовательно, при Δt→0 векторы Δvn и v становятся взаимно перпендикулярными. Т.к. вектор скорости направлен по касательной к траектории, то вектор Δvn, перпендикулярный вектору скорости, направлен к центру кривизны траектории точки. Вторая составляющая ускорения, равная

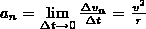
называется нормальной составляющей ускорения и направлена по прямой перпендикулярной касательной к траектории (называемой нормалью) к центру ее кривизны (поэтому ее называют также центростремительным ускорением).

Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис. 2):

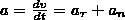
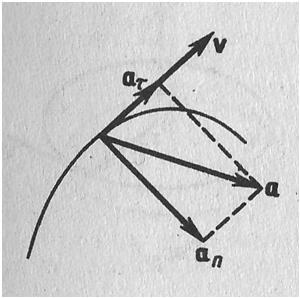
Рис.2

Значит тангенциальная составляющая ускорения является характеристикой быстроты изменения скорости по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения — характеристикой быстроты изменения скорости по направлению (направлена к центру кривизны траектории). В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:

1)aτ=0, an=0 — прямолинейное равномерное движение;

2)aτ=an=const, аn=0 - прямолинейное равнопеременное движение. При таком виде движения

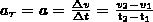
Если начальный момент времени t1 = 0, а начальная скорость v1 = v0, то, обозначив t2=t и v2 = v, получим a=(v-v0)/t, откуда

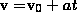
Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t найдем, что длина пути, пройденного точкой, в случае равнопеременного движения

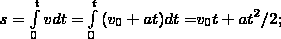
3)aτ=f(t), an=0 — прямолинейное движение с переменным ускорением;

4)aτ=0, an=const. При aτ=0 скорость по модулю не изменяется, а изменяется по направлению. Из формулы an=v2/r следует, что радиус кривизны должен быть постоянным. Следовательно, движение по окружности является равномерным;равномерное криволинейное движение;

5)aτ=0, an≠0 равномерное криволинейное движение;

6)aτ=const, an≠0 - криволинейное равнопеременное движение;

7)aτ=f(t), an≠0 - криволинейное движение с переменным ускорением.

№18 Уравнения касательной плоскости и нормали к поверхности

Определение. Пусть на области D задана функция двух переменных z =f(х,у), M0(x0;y0) - внутренняя точка области D, M(x0+Δx;y+Δy) - "соседняя" с M0 точка из D.

Рассмотрим полное приращение функции:

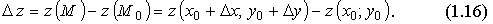
Если Δz представлено в виде:

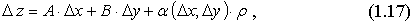
где A, B - постоянные (не зависящие от Δx, Δy), 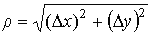- расстояние между M и M0, α(Δ x,Δy) - бесконечно малая при Δx 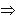0, Δy 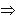0; тогда функция z =f(х,у) называется дифференцируемой в точке M0, а выражение

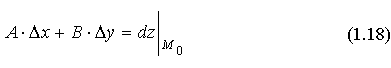
называется полным дифференциалом функции z =f(х;у) в точке M0.

Теорема 1.1. Если z =f(х;у) дифференцируема в точке M0, то

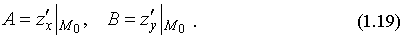
Доказательство

Так как в (1.16) Δx, Δy - произвольные бесконечно малые, то можно взять Δy =0, Δx≠0, Δx 0, тогда

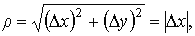
после чего из (1.16) следует

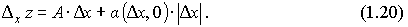
Тогда

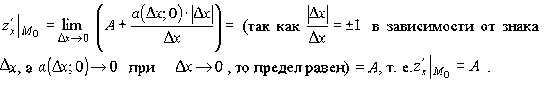
Аналогично доказывается, что

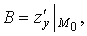
и теорема 1.1. доказана.

Замечание: из дифференцируемости z =f(х,у) в точке M0 следует существование частных производных. Обратное утверждение неверно (из существования частных производных в точке M0 не следует дифференцируемость в точке M0 ).

В итоге, с учётом теоремы 1.1 формула (1.18) примет вид:

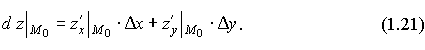
Следствие. Функция, дифференцируемая в точке M0, непрерывна в этой точке (так как из (1.17) следует, что при Δx 0, Δy 0: Δz 0, z(M) 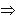z(M0)).

Замечание: Аналогично для случая трех и более переменных. Выражение (1.17) примет вид:

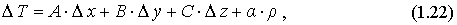
где

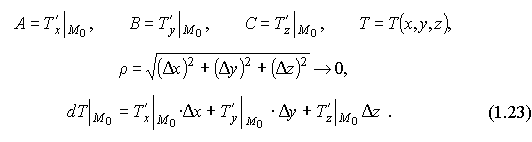
Используя геометрический смысл (рис.1.3) частных производных и можно получить следующее уравнение (1.24) касательной плоскости πкасs к поверхности: z =f(х,у) в точке C0(x0,y0,z0), z0=z(M):

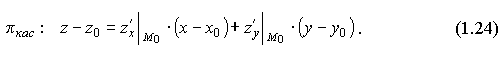
Из сравнения (1.24) и (1.21) получаем геометрический смысл полного дифференциала функции двух переменных:

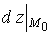
- приращение аппликаты z при движении точки С по касательной плоскости из точки С0 в точку

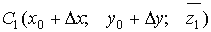
где 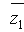находится из (1.24).

Уравнение нормали Lн к поверхности: z =f(х,у) в точке С0 получается, как уравнение прямой, проходящей через С0 перпендикулярно к касательной плоскости:

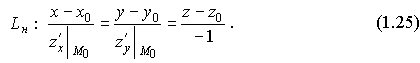
№ 19 Производная по направлению. Градиент

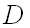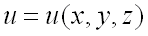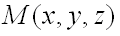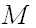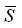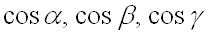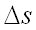Пусть в некоторой области задана функция и точка . Проведем из точки вектор , направляющие косинусы которого . На векторе , на расстоянии от его начала рассмотрим точку 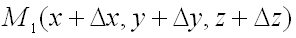, т.е. .

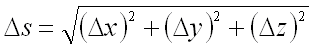Будем предполагать, что функция 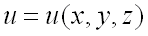и ее частные производные первого порядка непрерывны в области .

Предел отношения 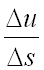при 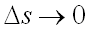называется производной от функции 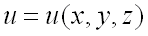в точке 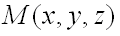по направлению вектора 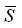и обозначается 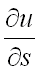, т.е. .

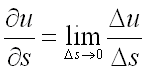Для нахождения производной от функции 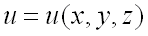в заданной точке 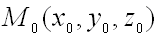по направлению вектора 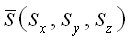используют формулу: ,

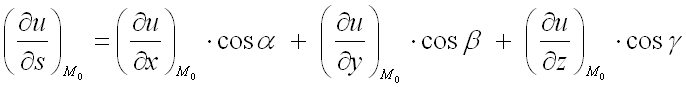где 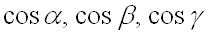– направляющие косинусы вектора 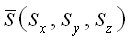, которые вычисляются по формулам: .

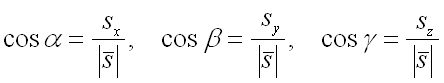Пусть в каждой точке некоторой области 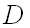задана функция .

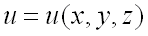Вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, называется градиентом функции 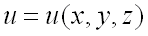и обозначается 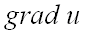или 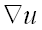(читается «набла у»): .

При этом говорят, что в области 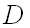определено векторное поле градиентов.

Для нахождения градиента функции 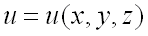в заданной точке 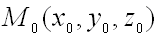используют формулу: .

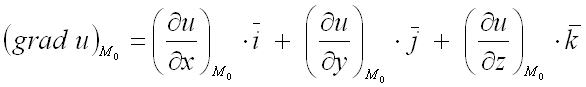№22 основные свойства неопределенного интеграла

Неопределенный интеграл

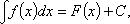
где F - первообразная функции f (на промежутке); C - произвольная постоянная.

Основные свойства

1.

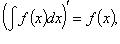
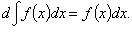
2.

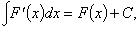
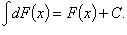
3. Если 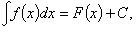то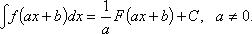

4.

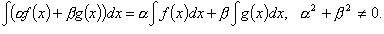
24)

25)

28)

Этот метод применяется в тех случаях, когда подынтегральное выражение представляет собой произведение или частное разнородных ф-ций. При этом за V’(x) принимается та часть, которая легко интегрируется.

29)

32)Разложение рациональной дроби на простейшие дроби.

Всякую правильную рациональную дробь 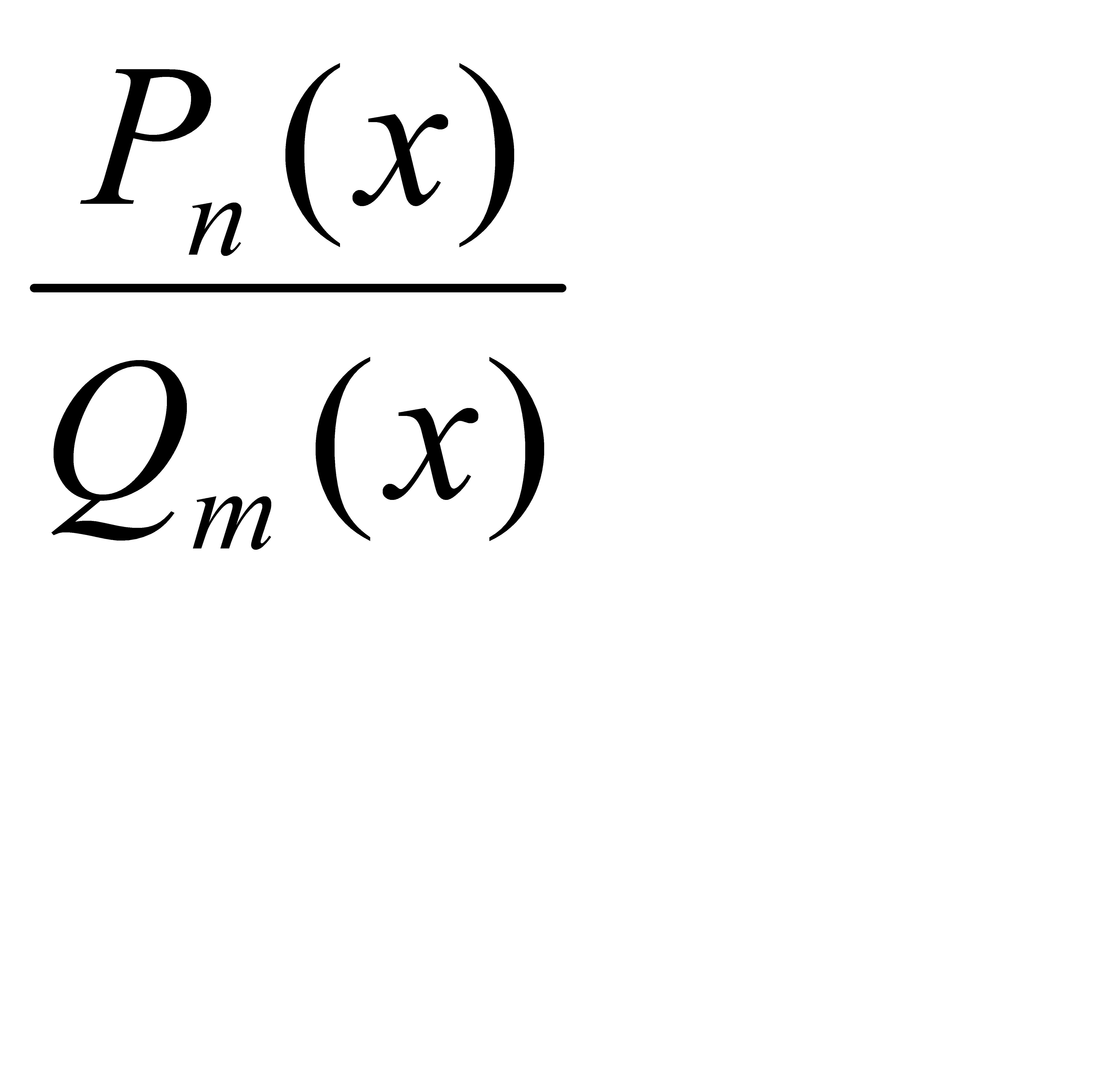можно представить в виде суммы конечного числа простейших рациональных дробей первого – четвертого типов. Для разложения 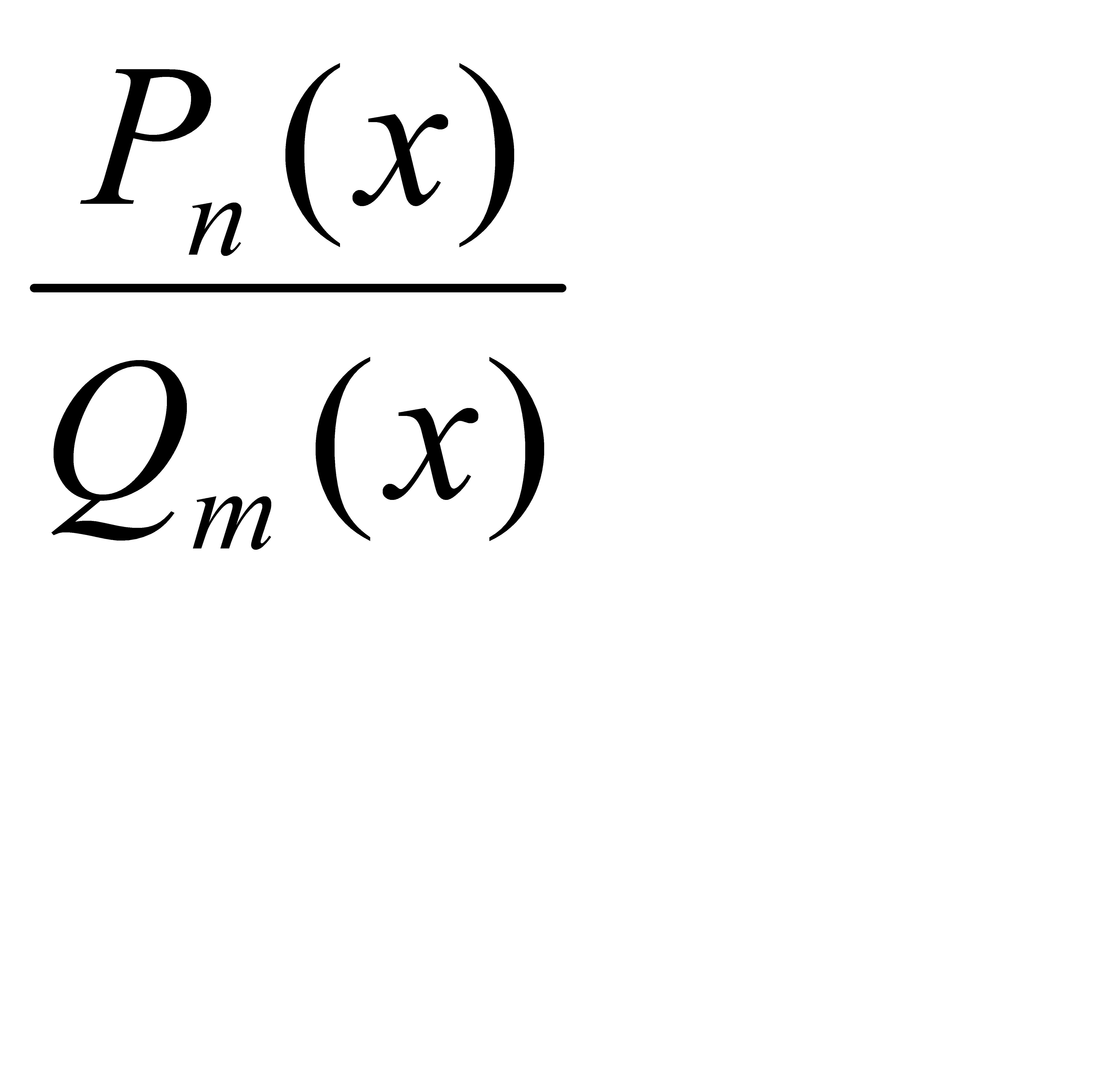на простейшие дроби необходимо разложить знаменатель Q_m(x) на линейные и квадратные множители, для чего надо решить уравнение:

- (5)

Теорема. Правильную рациональную дробь 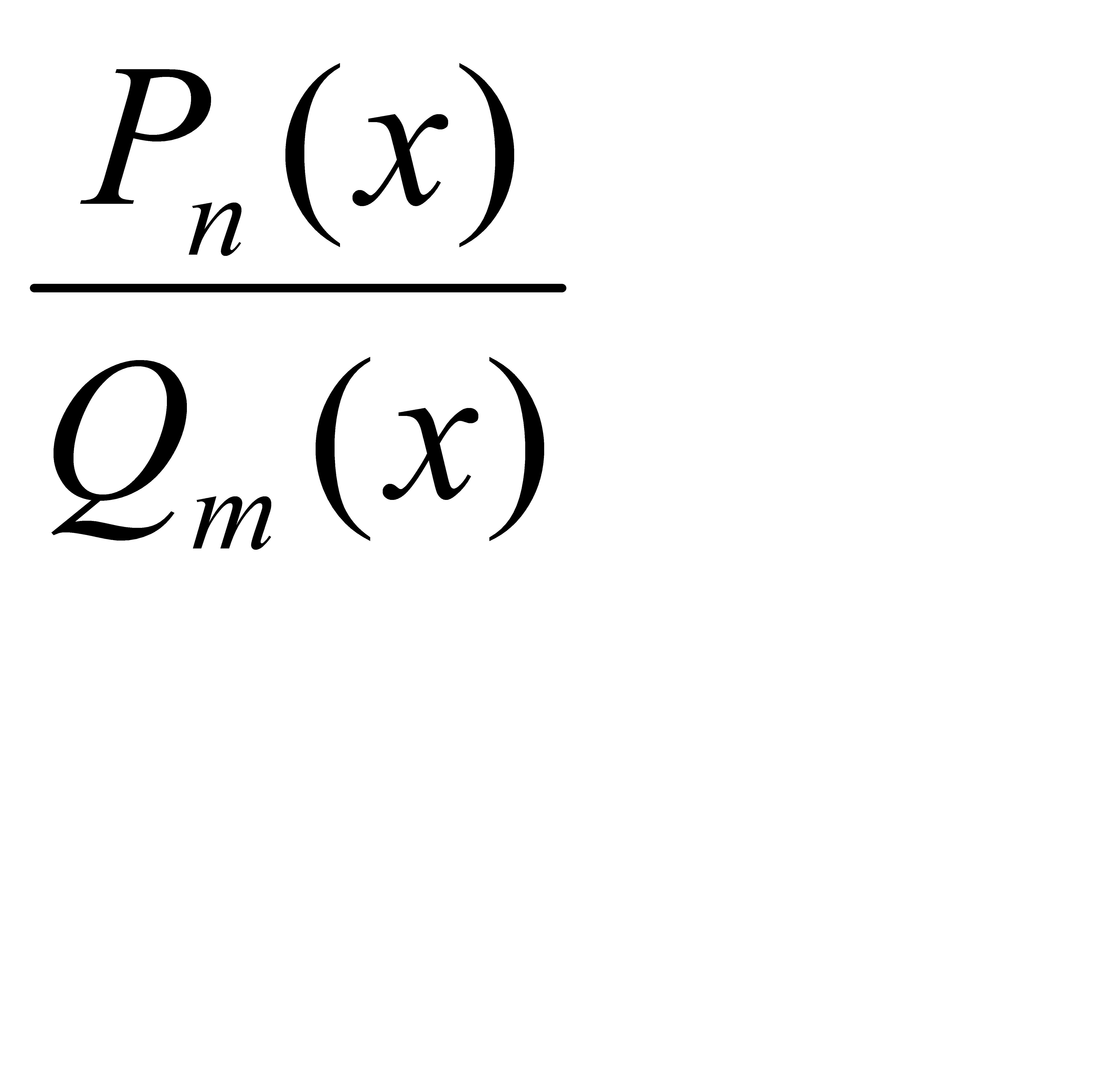, где , можно единственным образом разложить на сумму простейших дробей:

- (6)

(A₁, A₂, …, A_k, B₁, B₂, …, B₁, M₁, N₁, M₂, M₂, …, M_s, N_s – некоторые действительные числа).

33) Разложение правильной дроби на простейшие дроби при комплексных корнях знаменателя

Постановка задачи. Найти неопределенный интеграл

1. Введем обозначения:

.

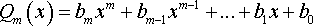
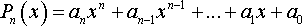
Сравним степени числителя и знаменателя .

Если подынтегральная функция – неправильная рациональная дробь, т.е. степень числителя n больше или равна степени знаменателя m, то сначала выделяем целую часть рациональной функции, поделив числитель на знаменатель:

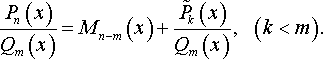
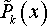
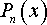
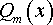
Здесь многочлен – остаток от деления на причем степень Pk(x) меньше степени Qm

2. Разложим правильную рациональную дробь

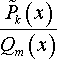
на элементарные дроби.

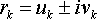Если ее знаменатель имеет простые комплексные корни т.е.

,

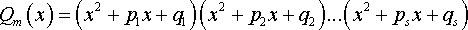
где

,

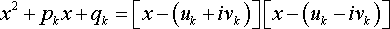
то разложение имеет вид

.

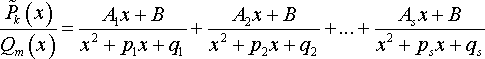
3. Для вычисления неопределенных коэффициентов ,A1,A2,A3...B1,B1,B3... приводим к общему знаменателю дроби в правой части тождества, после чего приравниваем коэффициенты при одинаковых степенях X в числителях слева и справа. Получим систему 2S уравнений с 2S неизвестными, которая имеет единственное решение.

4Интегрируем элементарные дроби вида

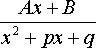
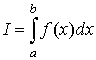47)Если существует конечный предел I интегральной суммы при λ → 0, и он не зависит от способа выбора точек ξ i, способа разбиения отрезка, то этот предел называется определенным интегралом от функции f (x)по отрезку [a, b] и обозначается следующим образом:

,

или

.

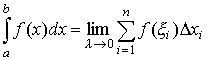
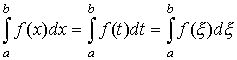В этом случае функция f (x) называется интегрируемой на [a, b]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f (x) – подынтегральной функцией, х – переменной интегрирования. Следует заметить, что не имеет значения, какой буквой обозначена переменная интегрирования определенного интеграла

,

поскольку смена обозначений такого рода никак не влияет на поведение интегральной суммы. Несмотря на сходство в обозначениях и терминологии, определенный и неопределенный интегралы различны

48)Теорема о существовании определённого интеграла

Разобьем отрезок [a, b] на части точками x1,x2,x3... так что

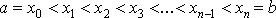
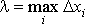Обозначим через deltaX длину i-го кусочка и через максимальную из этих длин.

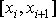
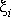
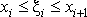Выберем на каждом отрезке произвольным образом некоторую точку так что (она называется «средней точкой»), и составим

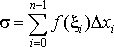
величину, которая называется интегральной суммой

Найдем теперь предел

.

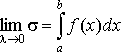
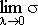
Определение. Если существует и он не зависит от

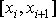а) способа разбиения отрезка на части и от

б) способа выбора средней точки,

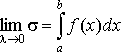
есть определенный интеграл от функции f(x) по отрезку [a, b].

Функция f(x) называется в этом случае интегрируемой на отрезке [a, b]. Величины a и b называются нижним и верхним пределами интегрирования соответственно.

50) Основные св-ва определённого интегрирала

1)Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

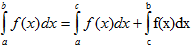
2)теорема о среднем значении.

Пусть функция y = f(x) интегрируема на отрезке [a; b],m=min f(x) и M=max f(x) , тогда существует такое число

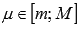
Что

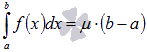
Следствие.

Если функция y = f(x) непрерывна на отрезке [a; b], то найдется такое число , что .

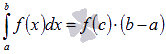
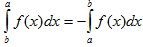3)При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

4)Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

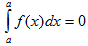
5)Интегрирование модуля функции

Если функция f(x) интегрируема,то и её модуль интегрируем на отрезке.

\

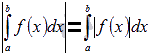
6)Интегрирование неравенства

Если f(x) и q(x) интегрируемы на отрезке [a;b] и х принадлежит [a;b]

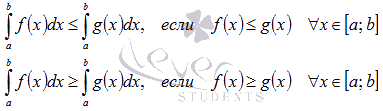то

7)Линейность

Постоянный множитель можно выносить за знак определенного интеграла

если f(x) существует и интегрируема на отрезке [a;b] , A=const

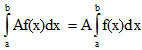
№51

Если функция y=f(x) непрерывна на отрезке [a;b] и F(x) – какая-либо ее первообразная на [a;b] (F’(x)=f(x)), то имеет место формула

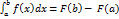
№52

Пусть для вычисления интеграла 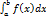от непрерывной функции сделана подстановка x=α(t).

Теорема:

Если:

1) Функция x=α(t) и ее производная x’=α’(t) непрерывны при t принадлежащей [c;v]

2) Множеством значений функции x=α(t) при t принадлежащей [c;v] является отрезок [a;b]

3) A α(c)=a и α(v)=b

То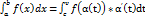

№55

Пусть функция f(x) непрерывна на промежутке [a;b] и имеет бесконечный разрыв при x=b. Если существует предел 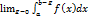, то его называют несобственным интегралом второго рода и обозначают .

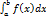Таким образом, по определению,

= .

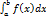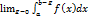Если предел в правой части существует, то несобственный интеграл 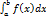сходится. Если же указанный предел не существует или бесконечен, то говорят, что интеграл 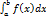расходится.