Интенсивность напряжений и интенсивность деформаций. Критерии пластичности
В теории пластичности большое значение имеют такие понятия, как девиаторы напряжений и деформаций, интенсивности напряжений и деформаций.
Остановимся на этих понятиях. Напомним, напряжение в точке и деформацию в точке можно представить в виде тензора напряжений Тн и тензора деформаций Тд.
Представим тензор напряжений Тн в виде суммы тензоров, Так, если напряженное состояние в точке представить в виде суммы напряженных состояний, определяемых равносторонним растяжением, напряжением σ0 =(σx +σy +σz)/3 и действием компонент напряжений σx – σ0 , σy – σ0, σz – σ0, τxy ,τyz , τzx , то общее напряженное состояв в тензорной форме представится в виде
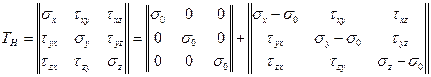 ,
,
или ТН= Тσ0 + Dσ, где
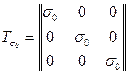
- шаровой тензор, а
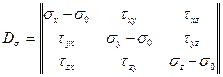
— девиатор напряжений.
Первое напряженное состояние, характеризуемое действием равностороннего растяжения или сжатия, приводит только к изменению объема и не изменяет формы. Второе напряженное состояние, характеризуемое девиатором напряжений, напротив, не изменяет величины объема, но изменяет форму выделенного из тела элемента.
Опыты показывают, что тело может испытывать очень большие величины равностороннего сжатия и оставаться при этом в упругом состоянии. Из этого следует, что за переход из упругого в пластическое состояние следует считать ответственным девиатор напряжений.
Интенсивностью напряжений называют величину
σi = 1/√2×√[(σx – σy)2 +(σy –σz)2 + (σz – σx)2 + 6( τ2xy + τ2yz +τ2zx)]
Интенсивностью касательных напряжений τi - называют величину, равную
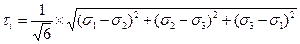
Между интенсивностью напряжений σi и интенсивностью касательных напряжений τi имеется следующая зависимость:
σi = √3 τi
Интенсивность касательных напряжений с точностью до числового множителя равна касательному напряжению на площадке, равнонаклоненной к направлениям главных
напряжений (рис. 1.9).
В самом деле, направление нормали v к этой площадке характеризуется следующими величинами направляющих косинусов:
cos(x,v) = cos(y,v) = cos(z,v) = 1/√3
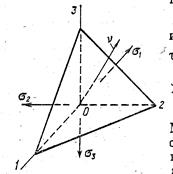
Рис. 1.9
Полное напряжение pv на этой площадке, называемой октаэдрической, будет равно
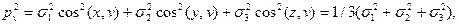
а нормальное напряжение σv к площадке
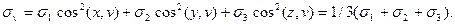
Касательное напряжение на октаэдрической площадке найдем из выражения
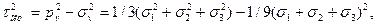
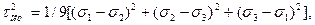
откуда
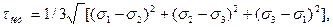
Следовательно,
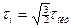 ,
, 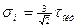
Таким образом, интенсивность напряжений можно интерпретировать как величину, пропорциональную октаэдрическому касательному напряжению.
Аналогично тому, как напряженное состояние в точке тела было представлено выше, в виде суммы двух напряженных состояний, деформированное состояние в этой точке, можно представить в виде суммы двух деформированных состояний — одного, определяемого равносторонним растяжением (сжатием), и второго, при котором компоненты деформаций получаются как разности действительного деформированного состояния и состояния всестороннего растяжения (сжатия).
Тензор деформации ТД можно представить в следующем виде
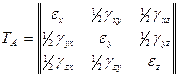
При всестороннем растяжении напряжениями σ0 =(σx +σy +σz)/3 деформации в направлении осей x, y, z будут одинаковы и равны
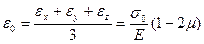
Тензор деформаций, соответствующий всестороннему растяжению, обозначим через Тε0:
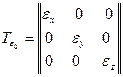 .
.
Девиатор деформаций
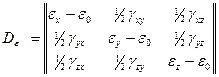
Таким образом, в общем виде тензор деформаций можно представить как сумму двух тензоров — шарового тензора деформаций и девиатора деформаций:
ТД = Тε0 + Dε
Шаровой тензор деформаций определяет изменение удельного объема в точке тела, а девиатор — изменение формы без изменения объема.
Пластические деформации, как показывают эксперименты, связаны с явлениями сдвига. Поэтому естественно, что и имеющие широкое распространение теории пластичности| в основе своей имеют сравнение некоторых касательных напряжений с предельными, вызывающими появление текучести.
Основываясь на опытах Треска по истечению металла через отверстия, Сен-Венан считал, что переход из yпругого состояния в пластическое в окрестности точки происходит тогда, когда максимальное касательное напряжение в точке достигает некоторого постоянного значения, xaрактерного для данного материала:
τmax= σT/2
или
σ1 - σ3 = σТ
Этот критерий пластичности соответствует известному из курса сопротивления материалов условию, вытекающему из теории прочности Кулона наибольших касательных
напряжений.
Другой распространенный в настоящее время критерий пластичности, предложенный Мизесом (он называется также критерием Губера — Мизеса), определяет переход упругого в пластическое состояние в окрестности точки при условии
σi = σТ
или
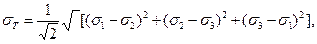
В этом случае не максимальное касательное напряжение, а октаэдрическое касательное напряжение достигает некоторого постоянного для данного материала предельного значения. Критерий пластичности Губера — Мизеса cooтветствует известному условию энергетической теории прочности.
Хотя результаты, получающиеся по этим двум критериям пластичности, достаточно близки, однако следует отметить, что многочисленные опыты, проведенные для плоского напряженного состояния, показывают, что экспериментальные результаты лучше согласуются с критерием пластичности Губера — Мизеса.
