Урок № 29. Контрольна робота № 2.

МІЖРЕГІОНАЛЬНЕ ВИЩЕ ПРОФЕСІЙНЕ УЧИЛИЩЕ З ПОЛІГРАФІЇ ТА ІНФОРМАЦІЙНИХ ТЕХНОЛОГІЙ

МЕТОДИЧНІ РЕКОМЕНДАЦІЇ

Для учнів

Напрям підготовки 186 «Видавництво та поліграфія»

Спеціальність 5.05150101 «Друкарське виробництво»

До виконання контрольних робіт

№ 1, № 2, № 3, № 4, № 5, № 6

З навчальної дисципліни

«ОСНОВИ ВИЩОЇ МАТЕМАТИКИ»

«Основи алгебри і геометрії»

«Диференціальні рівняння»

Дніпропетровськ

Зміст

Контрольна робота № 1 …………………………………………………. 3

Контрольна робота № 2 …………………………………………………. 8

Контрольна робота № 3 …………………………………………………. 15

Контрольна робота № 4 …………………………………………………. 22

Контрольна робота № 5 …………………………………………………. 29

Контрольна робота № 6 …………………………………………………. 36

Завдання для контрольних робіт …………………………………………. 38

Контрольна робота № 1.

Модуль 1. «Комплексні числа»

Модуль 2. «Лінійна алгебра»

Контрольна робота № 1 виконується учнями після вивчення наступних розділів програми:

· Комплексні числа і дії над ними.

· Форми запису комплексних чисел.

· Елементи теорії матриць.

· Загальна теоріясистем лінійних алгебраїчних рівнянь.

Розв’язування типових завдань

Завдання 1. Для комплексних чисел 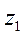та :

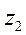а) знайти модуль та головне значення;

б) записати їх в тригонометричній та показникові формах;

в) обчислити суму, різницю, добуток та частку комплексних

чисел 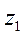та .

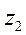► а) Знайдемо модуль та головне значення комплексних чисел 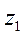та :

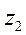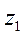: дійсна частина , уявна ; головне значення , , так як комплексне число 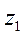розташоване в І чверті.

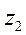: дійсна частина , уявна ; головне значення ,

, так як комплексне число 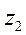розташоване в ІІ чверті.

б) Тригонометрична форма : маємо , ;

показникові форма : маємо , .

в) Обчислимо суму та різницю комплексних чисел за формулою

, маємо , ;

обчислимо добуток

;

Знайдемо частку комплексних чисел :

. ◄

Завдання 2. Розв’язати рівняння: а) ,

б) , в)

► а)

,

маємо : ,

;

б)

маємо : ,

;

в)

маємо : ,

. ◄

Завдання 3. Піднести до степеня: а) , б) , в)

► Виконаємо піднесення до степеня комплексних чисел в алгебраїчній формі:

а) для даного випадку використаємо формулу скороченого множення

.

Маємо .

б) запишемо умову завдання в вигляді

.

Маємо .

в) запишемо умову завдання в вигляді

.

Маємо . ◄

Завдання 4. Обчислити визначники матриць:

1) ; 2) ; 3) ; 4)

► В прикладах 1) та 2) обчислимо визначники матриці 2-го порядку за правилом .

1) ;

2) . ◄

► В прикладах 3) та 4) обчислимо визначники матриці 3-го порядку :

3) обчислимо визначник за правилом Саріуса

;

4) обчислимо визначник шляхом розкладання його за елементами 3-го рядка, так як один елемент рядка дорівнює нулю,

. ◄

Завдання 5. Розв’язати систему лінійних рівнянь методом Крамера:

1) ; 2) .

► 1) Запишемо і обчислимо основний визначник системи:

Так як основний визначник системи відмінний від нуля, то система має єдиний розв’язок, який знайдемо за допомогою формул Крамера. Обчислимо допоміжні визначники :

;

;

;

Використаємо формули Крамера :

; ;

Перевірка

Підставимо знайдені в ліві частини рівнянь заданої системи:

Сукупність чисел (3, 2, 1) являється єдиним розв`язком системи. ◄

► 2) Запишемо і обчислимо основний визначник системи:

Так як основний визначник системи відмінний від нуля, то система має єдиний розв’язок, який знайдемо за допомогою формул Крамера. Обчислимо допоміжні визначники :

;

;

Використаємо формули Крамера :

; ;

Перевірка

Підставимо знайдені в ліві частини рівнянь заданої системи:

Сукупність чисел (2, –1, 1) являється єдиним розв`язком системи. ◄

Урок № 29. Контрольна робота № 2.

Модуль 3. «Аналітична геометрія на площині».

Контрольна робота № 2 виконується учнями після вивчення наступних розділів програми:

· Пряма на площині.

· Криві другого порядку.

Завдання 1. Відомі вершини трикутника АВС: А(2, 5), В(1, 2),

С(4, 3). Знайти:

а) рівняння сторони АВ; б) довжину сторони АС ; в) кут В трикутника АВС; г) кут С трикутника АВС ; д) висоту ∆ АВС, проведеної з вершини А.

►

а) Використаємо формулу рівняння прямої, що проходить через дві точки:

АВ: ,

АВ: ,

АВ: .

б) Довжина сторони АС :

в) Для обчислення кута В використаємо формулу

Знайдемо рівняння сторони ВС :

Підставимо значення в рівняння ( 1 ):

г) Кут С утворюють сторони СА і СВ , то для знаходження кута С можна використати формулу , якщо рівняння сторін задані з кутовими коефіцієнтами.

, .

д) Висота ∆ АВС, проведеної з вершини А дорівнює відстані від точки А до сторони ВС, яку знаходимо за формулою , де

і ВС задана загальним рівнянням .

Підставимо числові значення в рівняння:

. ◄

Завдання 2. Привести задані рівняння еліпса до канонічного вигляду, обчислити їх осі, координати фокусів, ексцентриситет та знайти координати вершин. Виконати рисунок.

а) ; б) .

► а) Приведемо рівняння до канонічного виду

;

– канонічне рівняння еліпса, у якого , тому велика ( фокальна) вісь , мала вісь .

Фокуси даного еліпса лежать на осі : , , знайдемо значення с : .

Отже, – координати фокусів.

Ексцентриситет еліпса обчислимо за формулою , маємо .

Вершини еліпса .

Виконаємо рисунок

◄

► б) Приведемо рівняння до канонічного виду

;

– канонічне рівняння еліпса, у якого , тому велика ( фокальна) вісь , мала вісь .

Фокуси даного еліпса лежать на осі : , , знайдемо значення с : .

Отже, – координати фокусів.

Ексцентриситет еліпса обчислимо за формулою , маємо .

Вершини еліпса .

Виконаємо рисунок

◄

Завдання 3. Обчислити координати фокусів та вершин, ексцентриситет і рівняння асимптот заданої гіперболи. Виконати рисунок.

1) ; 2) .

► 1) , дійсна ( фокальна) вісь , уявна вісь .

Фокуси заданої гіперболи лежать на осі : , знайдемо значення с : .

Отже, – координати фокусів.

Ексцентриситет гіперболи обчислимо за формулою , маємо .

Вершини гіперболи , рівняння асимптот має вигляд , згідно умови отримаємо .

Виконаємо рисунок

◄

► 2) , дійсна ( фокальна) вісь , уявна вісь .

Фокуси заданої гіперболи лежать на осі : , знайдемо значення с : .

Отже, – координати фокусів.

Ексцентриситет гіперболи обчислимо за формулою , маємо .

Вершини гіперболи , рівняння асимптот має вигляд , згідно умови отримаємо .

Виконаємо рисунок

◄

Завдання 4. Знайти координати фокуса і рівняння директриси для заданої параболи. Виконати рисунок.

а) ; б) ; в) .

Параболи а) – в) мають віссю одну з координатних осей і вершина параболи знаходиться в початку координат.

► а) Запишемо рівняння параболи в вигляді , де р – параметр параболи : , . За видом рівняння парабола симетрична відносно осі абсцис, а так як перед параметром стоїть знак «– », то гілки параболи направлені вліво. Відстань між директрисою і фокусом дорівнює і вони рівновіддалені від вершини (початку координат), то координати фокуса тобто .

Директриса – пряма перпендикулярна осі параболи, то її рівняння має вигляд тобто .

Виконаємо рисунок

◄

► б) Запишемо рівняння параболи в вигляді , де р – параметр параболи : , . За видом рівняння парабола симетрична відносно осі ординат , а так як перед параметром стоїть знак «+», то гілки параболи направлені вверх. Відстань між директрисою і фокусом дорівнює і вони рівновіддалені від вершини (початку координат), то координати фокуса тобто .

Директриса – пряма перпендикулярна осі параболи, то її рівняння має вигляд тобто .

Виконаємо рисунок

◄

► в) Запишемо рівняння параболи в вигляді , де р – параметр параболи : , . За видом рівняння парабола симетрична відносно осі абсцис, а так як перед параметром стоїть знак «+ », то гілки параболи направлені вправо. Відстань між директрисою і фокусом дорівнює і вони рівновіддалені від вершини (початку координат), то координати фокуса тобто .

Директриса – пряма перпендикулярна осі параболи, то її рівняння має вигляд тобто .

Виконаємо рисунок

◄

Контрольна робота № 3